
- •1.Масса.Сила.Импульс тела и импульс силы. Закон сохранения и изменения импульса.
- •2.Центр инерции. Закон движения центра масс.
- •3.Движение тела в переменной массой . Выведение уравнения Мещерского
- •4.24.Консервативные силы. Потенциальная энергия. Связь между потенц. Энергией и силой.
- •5. Какое силовое поле называют потенциальным? Докажите, что однородное и центральное силовые поля являются потенциальными. Как определяется сила через потенциальную энергию?
- •6. Что называют механической энергией? Сформулируйте закон ее сохранения. Дайте определение кинетической и потенциальной энергий и выведите закон сохранения энергии в механике.
- •7.Механическая работа. Мощность. Кинетическая и потенциальная энергия тела. Закон сохранения и изменения механической энергии.
- •9.Сформулируйте постулаты специальной теории относительности. Запишите преобразования Лоренца для координат и времени. Как связаны длины и промежутки времени в разных системах отсчета?
- •10. Сформулируйте постулаты специальной теории относительности. Дайте определение интервала между событиями и докажите его инвариантность относительно преобразований Лоренца.
- •11. Запишите преобразования Лоренца для координат и времени. Выведите из них закон сложения скоростей в релятивистской механике.
- •12. Как рассчитывается кинетическая энергия релятивистской частицы, полная энергия и энергия покоя. Взаимосвязь полной энергии и импульса.
- •13. Уравнение движения тела в неинерциальных системах отсчета. Что такое силы инерции? Классифицируйте силы инерции по характеру движения неинерциальной системы отсчета и тела в ней.
- •14. Момент инерции. Вывести формулу для момента инерции сплошного диска относительно оси симметрии. Теорема Штейнера, ее вывод.
- •15. Момент инерции тела относительно оси. Доказательство теоремы Штейнера. Моменты инерции однородных тел (стержня, цилиндра, шара) относительно осей симметрии.
- •17. Что называют моментом импульса системы относительно данной точки? Выведите закон изменения момента импульса системы частиц. Сформулируйте закон сохранения момента импульса.
- •18. Пружинный маятник. Выведите дифференциальное уравнение его свободных незатухающих колебаний и запишите его решение.
- •19. Математический и пружинный маятники. Вывод формулы для расчета периодов их свободных незатухающих колебаний.
- •20. Физический маятник. Его приведенная длина. Вывод формулы для расчета периода его свободных незатухающих колебаний.
- •26. Выведите дифференциальное уравнение затухающих гармонических колебаний и запишите его решение. Дайте определение логарифмического декремента затухания.
- •27. Какие колебания называют вынужденными? Запишите дифференциальное уравнение вынужденных колебаний и его решение. Резонанс. Выведите формулу для расчета резонансной частоты.
- •29. Что такое волна? Уравнение бегущей плоской гармонической волны.
- •32. Получите уравнение стоячей волны. Пучности и узлы, условия их расположения.
- •33. Что такое волна? Уравнение плоской бегущей гармонической волны. В чем состоит эффект Доплера? Выведите формулу для частоты волны при движении ее источника и приемника.
- •36. Выведите барометрическую формулу. Получите из нее закон Больцмана для распределения частиц во внешнем силовом потенциальном поле.
- •38. Теплоемкость тела. Удельная и молярная теплоемкость, связь между ними. Классическая теория теплоемкости идеального газа и ее недостатки.
- •39. Объясните явление теплопроводности. Выведите закон Фурье. Поясните физический смысл коэффициента теплопроводности.
- •40. Объясните явление диффузии. Выведите закон Фика. Поясните физический смысл коэффициента диффузии.
- •41. Явления переноса. Выведите закон Фика. Получите выражение для коэффициента диффузии через усредненные характеристики теплового движения молекул.
- •42. Объясните явление вязкости. Выведите формулу Ньютона для силы вязкого трения. Объясните физический смысл коэффициента вязкости.
- •43. Адиабатный процесс. Вывод закона Пуассона. Работа газа в адиабатном процессе.
- •46. Энтропия. Определение энтропии через термодинамическую вероятность. Приведите различные формулировки второго закона термодинамики.
- •47. Приведите различные формулировки второго закона термодинамики. Теорема Нернста.
- •48.49. Реальные газы. Сила и потенциальная энергия межмолекулярного взаимодействия. Уравнение и изотермы Ван-дер-Ваальса.
- •50. Фаза, фазовые переходы между агрегатными состояниями вещества. Фазовые переходы 1 и 2 рода.
18. Пружинный маятник. Выведите дифференциальное уравнение его свободных незатухающих колебаний и запишите его решение.
Пружинный
маятник —
это груз массой т, подвешенный на
абсолютно упругой пружине и совершающий
гармонические колебания под действием
упругой силы F=-kx,
где k
— жесткость пружины. Уравнение движения
маятника
![]()
Выведение: Если можно пренебречь силами сопротивления движению и трением, то при выведении системы из положения равновесия на груз будет действовать только сила упругости пружины.
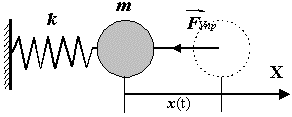 Запишем уравнение
движения груза, составленное по 2-му
закону Ньютона:
Запишем уравнение
движения груза, составленное по 2-му
закону Ньютона:
![]() Спроектируем
уравнение движения на ось X,
при этом учтем, что сила упругости
пропорциональна смещению из положения
равновесия и направлена в сторону ему
противоположную, а ускорение - это вторая
производная координаты по времени.
Тогда:
Спроектируем
уравнение движения на ось X,
при этом учтем, что сила упругости
пропорциональна смещению из положения
равновесия и направлена в сторону ему
противоположную, а ускорение - это вторая
производная координаты по времени.
Тогда:
![]() (1).
Преобразуем выражение (1) к виду
(1).
Преобразуем выражение (1) к виду
 Введем
обозначение
Введем
обозначение  (частота
собственных незатухающих
колебаний или собственная
частота),
окончательно получим
(частота
собственных незатухающих
колебаний или собственная
частота),
окончательно получим
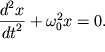 (2).
Выражение (2) - это дифференциальное
уравнение свободных
гармонических незатухающих колебаний.
(2).
Выражение (2) - это дифференциальное
уравнение свободных
гармонических незатухающих колебаний.
Решение
уравнения (2) будем искать в виде:
![]() (3).
Подставим (3) в (2) получим
(3).
Подставим (3) в (2) получим
![]() Из
полученного выражения найдем значения
Из
полученного выражения найдем значения ![]() :
:
![]() (4)
где
(4)
где ![]() Тогда
Тогда
![]() .
.
19. Математический и пружинный маятники. Вывод формулы для расчета периодов их свободных незатухающих колебаний.
Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити.
Вывод:
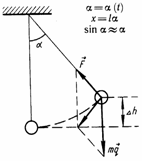 На
тело действуют сила тяжести и сила
натяжения нити. Равнодействующая этих
сил имеет две составляющие: тангенциальную,
меняющую ускорение по величине, и
нормальную, меняющую ускорение по
направлению (центростремительное
ускорение, тело движется по дуге). Т.к.
угол мал, то тангенциальная составляющая
равна проекции силы тяжести на касательную
к траектории:
На
тело действуют сила тяжести и сила
натяжения нити. Равнодействующая этих
сил имеет две составляющие: тангенциальную,
меняющую ускорение по величине, и
нормальную, меняющую ускорение по
направлению (центростремительное
ускорение, тело движется по дуге). Т.к.
угол мал, то тангенциальная составляющая
равна проекции силы тяжести на касательную
к траектории: ![]() .
Угол в радианах равен отношению длины
дуги к радиусу (длине нити), а длина дуги
приблизительно равна смещению
(x »s):
.
Угол в радианах равен отношению длины
дуги к радиусу (длине нити), а длина дуги
приблизительно равна смещению
(x »s): ![]() .Сравним
полученное уравнение с уравнением
колебательного движения
.Сравним
полученное уравнение с уравнением
колебательного движения ![]() .
.
Видно,
что ![]() или
или ![]() -
циклическая частота при колебаниях
математического маятника.
-
циклическая частота при колебаниях
математического маятника.
Период
колебаний 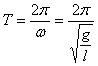 или
или  (формула
Галилея).
Пружинный
маятник —
это груз массой т, подвешенный на
абсолютно упругой пружине и совершающий
гармонические колебания под действием
упругой силы F=-kx,
где k
— жесткость пружины.
В вертикальном
положении на груз на пружине действуют
сила тяжести и сила упругости пружины.
Под действием силы тяжести пружина
растягивается на х1,
а затем мы отклоняем его от этого
положения на х.
Тогда согласно
второму закону Ньютона, учитывая знаки
проекций, получим:
(формула
Галилея).
Пружинный
маятник —
это груз массой т, подвешенный на
абсолютно упругой пружине и совершающий
гармонические колебания под действием
упругой силы F=-kx,
где k
— жесткость пружины.
В вертикальном
положении на груз на пружине действуют
сила тяжести и сила упругости пружины.
Под действием силы тяжести пружина
растягивается на х1,
а затем мы отклоняем его от этого
положения на х.
Тогда согласно
второму закону Ньютона, учитывая знаки
проекций, получим: ![]() .
Но
.
Но ![]() ,
тогда:
,
тогда: ![]() .
.
Или ![]() -
ускорение тела, колеблющегося на пружине,
не зависит от силы тяжести, действующей
на это тело. Сила тяжести только приводит
к изменению положения равновесия.
-
ускорение тела, колеблющегося на пружине,
не зависит от силы тяжести, действующей
на это тело. Сила тяжести только приводит
к изменению положения равновесия.
Выразим
ускорение:![]() .
Сравним полученное уравнение с уравнением
колебательного движения
.
Сравним полученное уравнение с уравнением
колебательного движения ![]() .
Видно,
что
.
Видно,
что ![]() или
или ![]() -
циклическая частота при колебаниях
пружинного маятника.
Период
колебаний
-
циклическая частота при колебаниях
пружинного маятника.
Период
колебаний 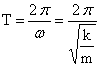 или
или ![]() (формула
Гюйгенса).
(формула
Гюйгенса).
