
- •1.Масса.Сила.Импульс тела и импульс силы. Закон сохранения и изменения импульса.
- •2.Центр инерции. Закон движения центра масс.
- •3.Движение тела в переменной массой . Выведение уравнения Мещерского
- •4.24.Консервативные силы. Потенциальная энергия. Связь между потенц. Энергией и силой.
- •5. Какое силовое поле называют потенциальным? Докажите, что однородное и центральное силовые поля являются потенциальными. Как определяется сила через потенциальную энергию?
- •6. Что называют механической энергией? Сформулируйте закон ее сохранения. Дайте определение кинетической и потенциальной энергий и выведите закон сохранения энергии в механике.
- •7.Механическая работа. Мощность. Кинетическая и потенциальная энергия тела. Закон сохранения и изменения механической энергии.
- •9.Сформулируйте постулаты специальной теории относительности. Запишите преобразования Лоренца для координат и времени. Как связаны длины и промежутки времени в разных системах отсчета?
- •10. Сформулируйте постулаты специальной теории относительности. Дайте определение интервала между событиями и докажите его инвариантность относительно преобразований Лоренца.
- •11. Запишите преобразования Лоренца для координат и времени. Выведите из них закон сложения скоростей в релятивистской механике.
- •12. Как рассчитывается кинетическая энергия релятивистской частицы, полная энергия и энергия покоя. Взаимосвязь полной энергии и импульса.
- •13. Уравнение движения тела в неинерциальных системах отсчета. Что такое силы инерции? Классифицируйте силы инерции по характеру движения неинерциальной системы отсчета и тела в ней.
- •14. Момент инерции. Вывести формулу для момента инерции сплошного диска относительно оси симметрии. Теорема Штейнера, ее вывод.
- •15. Момент инерции тела относительно оси. Доказательство теоремы Штейнера. Моменты инерции однородных тел (стержня, цилиндра, шара) относительно осей симметрии.
- •17. Что называют моментом импульса системы относительно данной точки? Выведите закон изменения момента импульса системы частиц. Сформулируйте закон сохранения момента импульса.
- •18. Пружинный маятник. Выведите дифференциальное уравнение его свободных незатухающих колебаний и запишите его решение.
- •19. Математический и пружинный маятники. Вывод формулы для расчета периодов их свободных незатухающих колебаний.
- •20. Физический маятник. Его приведенная длина. Вывод формулы для расчета периода его свободных незатухающих колебаний.
- •26. Выведите дифференциальное уравнение затухающих гармонических колебаний и запишите его решение. Дайте определение логарифмического декремента затухания.
- •27. Какие колебания называют вынужденными? Запишите дифференциальное уравнение вынужденных колебаний и его решение. Резонанс. Выведите формулу для расчета резонансной частоты.
- •29. Что такое волна? Уравнение бегущей плоской гармонической волны.
- •32. Получите уравнение стоячей волны. Пучности и узлы, условия их расположения.
- •33. Что такое волна? Уравнение плоской бегущей гармонической волны. В чем состоит эффект Доплера? Выведите формулу для частоты волны при движении ее источника и приемника.
- •36. Выведите барометрическую формулу. Получите из нее закон Больцмана для распределения частиц во внешнем силовом потенциальном поле.
- •38. Теплоемкость тела. Удельная и молярная теплоемкость, связь между ними. Классическая теория теплоемкости идеального газа и ее недостатки.
- •39. Объясните явление теплопроводности. Выведите закон Фурье. Поясните физический смысл коэффициента теплопроводности.
- •40. Объясните явление диффузии. Выведите закон Фика. Поясните физический смысл коэффициента диффузии.
- •41. Явления переноса. Выведите закон Фика. Получите выражение для коэффициента диффузии через усредненные характеристики теплового движения молекул.
- •42. Объясните явление вязкости. Выведите формулу Ньютона для силы вязкого трения. Объясните физический смысл коэффициента вязкости.
- •43. Адиабатный процесс. Вывод закона Пуассона. Работа газа в адиабатном процессе.
- •46. Энтропия. Определение энтропии через термодинамическую вероятность. Приведите различные формулировки второго закона термодинамики.
- •47. Приведите различные формулировки второго закона термодинамики. Теорема Нернста.
- •48.49. Реальные газы. Сила и потенциальная энергия межмолекулярного взаимодействия. Уравнение и изотермы Ван-дер-Ваальса.
- •50. Фаза, фазовые переходы между агрегатными состояниями вещества. Фазовые переходы 1 и 2 рода.
38. Теплоемкость тела. Удельная и молярная теплоемкость, связь между ними. Классическая теория теплоемкости идеального газа и ее недостатки.
Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малогоколичества теплоты δQ, полученного телом, к соответствующему приращению его температуры δT. Единица измерения теплоёмкости в системе СИ — Дж/К.
Удельная
теплоемкость вещества
— величина, равная количеству теплоты,
необходимому для нагревания 1 кг
вещества на 1 К:
![]() Единица удельной теплоемкости — джоуль
на килограмм-кельвин (Дж/(кг
К)).
Единица удельной теплоемкости — джоуль
на килограмм-кельвин (Дж/(кг
К)).
Молярная
теплоемкость—величина,
равная количеству теплоты, необходимому
для нагревания 1 моль вещества на 1 К:![]() (53.1), где =m/М—количество
вещества. Единица молярной теплоемкости
— джоуль на моль-кельвин (Дж/(моль
К)).
(53.1), где =m/М—количество
вещества. Единица молярной теплоемкости
— джоуль на моль-кельвин (Дж/(моль
К)).
Удельная
теплоемкость с связана с молярной Сm,
соотношением
![]() (53.2)
(53.2)
Различают теплоемкости при постоянном объеме и постоянном давлении.
Запишем
выражение первого начала термодинамики
для 1 моль газа с учетом формул
![]() и
(53.1):
и
(53.1):
![]() (53.3). Если газ нагревается при постоянном
объеме, то работа внешних сил равна нулю
и сообщаемая газу извне теплота вдет
только на увеличение его внутренней
энергии:
(53.3). Если газ нагревается при постоянном
объеме, то работа внешних сил равна нулю
и сообщаемая газу извне теплота вдет
только на увеличение его внутренней
энергии:
![]() (53.4), т. е. молярная
теплоемкость газа при постоянном объеме
СV
равна изменению внутренней энергии
1 моль газа при повышении его температуры
на 1 К. Согласно формуле (50.1),
(53.4), т. е. молярная
теплоемкость газа при постоянном объеме
СV
равна изменению внутренней энергии
1 моль газа при повышении его температуры
на 1 К. Согласно формуле (50.1),
![]() тогда
тогда
![]() (53.5). Если газ нагревается при постоянном
давлении, то выражение (53.3) можно записать
в виде
(53.5). Если газ нагревается при постоянном
давлении, то выражение (53.3) можно записать
в виде
![]() Учитывая,
что
Учитывая,
что
![]() не зависит от вида процесса (внутренняя
энергия идеального газа не зависит ни
от p,
ни от V, а определяется лишь температурой
Т) и всегда равна СV
(см. (53.4)), и дифференцируя уравнение
Клапейрона — Менделеева pVm=RT
(42.4) по T
(p=const),
получаем
не зависит от вида процесса (внутренняя
энергия идеального газа не зависит ни
от p,
ни от V, а определяется лишь температурой
Т) и всегда равна СV
(см. (53.4)), и дифференцируя уравнение
Клапейрона — Менделеева pVm=RT
(42.4) по T
(p=const),
получаем
![]() (53.6).Выражение (53.6) называется уравнением
Майера
(53.6).Выражение (53.6) называется уравнением
Майера
![]() (53.7). При рассмотрении
термодинамических процессов важно
знать характерное для каждого газа
отношение Сp
к СV
:
(53.7). При рассмотрении
термодинамических процессов важно
знать характерное для каждого газа
отношение Сp
к СV
:
![]() (53.8)
(53.8)
Недостатком является то, что СV зависит и от температуры: при низкой температуре (50 К) СV =3/2 R, при комнатной — CV = 5/2R (вместо расчетных 7/2R) и при очень высокой — Сv=7/2 R. Получается расхождение теории и эксперимента.
39. Объясните явление теплопроводности. Выведите закон Фурье. Поясните физический смысл коэффициента теплопроводности.
Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т. е., иными словами, выравнивание температур.
Вывод: Рассмотрим газ, заключѐнный между двумя параллельными
стенками, имеющими разную температуру Та и Тб. У нас
имеется
градиент температуры
 ,
тогда через газ в направлении
,
тогда через газ в направлении
оси х будет идти поток тепла. Хаотично двигаясь, молекулы будут
переходить из одного слоя газа в другой, перенося с собой энергию. Это
движение молекул приводит к перемешиванию молекул, имеющих
различную
кинетическую энергию
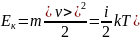 ,
здесь i – число
,
здесь i – число
степеней свободы молекулы. При подсчѐте потока тепла введѐм следующие упрощения:
1) среднеарифметическая скорость теплового движения молекул постоянна; 2)концентрация молекул в соседних слоях одинакова (хотя на самом
деле она различается, что даѐт ошибку ͌ 10 %). Через площадку dS за время dt слева
проходит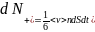 молекул. Средняя энергия этих молекул
К
молекул. Средняя энергия этих молекул
К
соответствует значению энергии в том месте, где они испытывают
последний
раз столкновение. Для одной молекулы
газа:
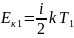 .
Соответственно, справа проходит
.
Соответственно, справа проходит
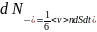 молекул. Каждая из этих молекул перенесѐт
энергию
молекул. Каждая из этих молекул перенесѐт
энергию
 .
Результирующий поток энергии через dS
равен разности потоков
.
Результирующий поток энергии через dS
равен разности потоков
dQ+ и dQ-, то есть . Применяя те же рассуждения, получим: результирующий тепловой поток через единичную площадку в единицу времени равен q и направлен он в сторону противоположную направлению градиента:
.
– закон Ж.Фурье для теплопроводности.
Коэффициент теплопроводности l показывает, какое количество тепла проходит вследствие теплопроводности в единицу времени через единицу поверхности теплообмена при падении температуры на 1 град на единицу длины нормали к изотермической поверхности.
