
- •1.Масса.Сила.Импульс тела и импульс силы. Закон сохранения и изменения импульса.
- •2.Центр инерции. Закон движения центра масс.
- •3.Движение тела в переменной массой . Выведение уравнения Мещерского
- •4.24.Консервативные силы. Потенциальная энергия. Связь между потенц. Энергией и силой.
- •5. Какое силовое поле называют потенциальным? Докажите, что однородное и центральное силовые поля являются потенциальными. Как определяется сила через потенциальную энергию?
- •6. Что называют механической энергией? Сформулируйте закон ее сохранения. Дайте определение кинетической и потенциальной энергий и выведите закон сохранения энергии в механике.
- •7.Механическая работа. Мощность. Кинетическая и потенциальная энергия тела. Закон сохранения и изменения механической энергии.
- •9.Сформулируйте постулаты специальной теории относительности. Запишите преобразования Лоренца для координат и времени. Как связаны длины и промежутки времени в разных системах отсчета?
- •10. Сформулируйте постулаты специальной теории относительности. Дайте определение интервала между событиями и докажите его инвариантность относительно преобразований Лоренца.
- •11. Запишите преобразования Лоренца для координат и времени. Выведите из них закон сложения скоростей в релятивистской механике.
- •12. Как рассчитывается кинетическая энергия релятивистской частицы, полная энергия и энергия покоя. Взаимосвязь полной энергии и импульса.
- •13. Уравнение движения тела в неинерциальных системах отсчета. Что такое силы инерции? Классифицируйте силы инерции по характеру движения неинерциальной системы отсчета и тела в ней.
- •14. Момент инерции. Вывести формулу для момента инерции сплошного диска относительно оси симметрии. Теорема Штейнера, ее вывод.
- •15. Момент инерции тела относительно оси. Доказательство теоремы Штейнера. Моменты инерции однородных тел (стержня, цилиндра, шара) относительно осей симметрии.
- •17. Что называют моментом импульса системы относительно данной точки? Выведите закон изменения момента импульса системы частиц. Сформулируйте закон сохранения момента импульса.
- •18. Пружинный маятник. Выведите дифференциальное уравнение его свободных незатухающих колебаний и запишите его решение.
- •19. Математический и пружинный маятники. Вывод формулы для расчета периодов их свободных незатухающих колебаний.
- •20. Физический маятник. Его приведенная длина. Вывод формулы для расчета периода его свободных незатухающих колебаний.
- •26. Выведите дифференциальное уравнение затухающих гармонических колебаний и запишите его решение. Дайте определение логарифмического декремента затухания.
- •27. Какие колебания называют вынужденными? Запишите дифференциальное уравнение вынужденных колебаний и его решение. Резонанс. Выведите формулу для расчета резонансной частоты.
- •29. Что такое волна? Уравнение бегущей плоской гармонической волны.
- •32. Получите уравнение стоячей волны. Пучности и узлы, условия их расположения.
- •33. Что такое волна? Уравнение плоской бегущей гармонической волны. В чем состоит эффект Доплера? Выведите формулу для частоты волны при движении ее источника и приемника.
- •36. Выведите барометрическую формулу. Получите из нее закон Больцмана для распределения частиц во внешнем силовом потенциальном поле.
- •38. Теплоемкость тела. Удельная и молярная теплоемкость, связь между ними. Классическая теория теплоемкости идеального газа и ее недостатки.
- •39. Объясните явление теплопроводности. Выведите закон Фурье. Поясните физический смысл коэффициента теплопроводности.
- •40. Объясните явление диффузии. Выведите закон Фика. Поясните физический смысл коэффициента диффузии.
- •41. Явления переноса. Выведите закон Фика. Получите выражение для коэффициента диффузии через усредненные характеристики теплового движения молекул.
- •42. Объясните явление вязкости. Выведите формулу Ньютона для силы вязкого трения. Объясните физический смысл коэффициента вязкости.
- •43. Адиабатный процесс. Вывод закона Пуассона. Работа газа в адиабатном процессе.
- •46. Энтропия. Определение энтропии через термодинамическую вероятность. Приведите различные формулировки второго закона термодинамики.
- •47. Приведите различные формулировки второго закона термодинамики. Теорема Нернста.
- •48.49. Реальные газы. Сила и потенциальная энергия межмолекулярного взаимодействия. Уравнение и изотермы Ван-дер-Ваальса.
- •50. Фаза, фазовые переходы между агрегатными состояниями вещества. Фазовые переходы 1 и 2 рода.
36. Выведите барометрическую формулу. Получите из нее закон Больцмана для распределения частиц во внешнем силовом потенциальном поле.
Выведем
закон изменения давления с высотой,
предполагая, что поле тяготения однородно,
температура постоянна и масса всех
молекул одинакова. Если атмосферное
давление на высоте h
равно р (рис. 67), то на высоте h+dh
оно равно p+dp (при dh>0
dp<0,
так как давление с высотой убывает).
Разность давлений р и p+dp равна весу
газа, заключенного в объеме цилиндра
высотой dh
с основанием площадью 1 м2:
![]() где
— плотность газа на высоте h (dh настолько
мало, что при изменении высоты в этом
пределе плотность газа можно считать
постоянной). Следовательно,
где
— плотность газа на высоте h (dh настолько
мало, что при изменении высоты в этом
пределе плотность газа можно считать
постоянной). Следовательно,
![]() (45.1). Воспользовавшись уравнением
состояния идеального газа pV=(m/M)
RT
(т — масса газа, М — молярная масса
газа), находим, что
(45.1). Воспользовавшись уравнением
состояния идеального газа pV=(m/M)
RT
(т — масса газа, М — молярная масса
газа), находим, что
![]()
Подставив
это выражение в (45.1), получим
![]()
С изменением высоты от h1 до h2 давление изменяется от р1 до р2 (рис. 67), т. е.
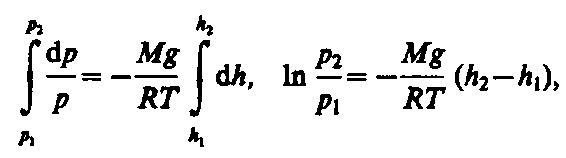 или
или
![]() (45.2)
(45.2)
![]() (45.3)
(45.3)
Выражение (45.2) называется барометрической формулой.
Барометрическую формулу (45.3) можно преобразовать, если воспользоваться выражением p=nkT:
![]() где n
– концентрация молекул на высоте h,
n0
– то же, на высоте h=0.
Так как M=m0NA
(NA
– постоянная Авогадро, т0
– масса одной молекулы), a
R=kNA,
то
где n
– концентрация молекул на высоте h,
n0
– то же, на высоте h=0.
Так как M=m0NA
(NA
– постоянная Авогадро, т0
– масса одной молекулы), a
R=kNA,
то
![]() (45.4), где m0gh=П
— потенциальная энергия молекулы в
поле тяготения, т. е.
(45.4), где m0gh=П
— потенциальная энергия молекулы в
поле тяготения, т. е.
![]() 45.5)
45.5)
Выражение (45.5) называется распределением Больцмана для внешнего потенциального поля.
37.Что
называют числом степеней свободы
молекулы? Чему оно равно для молекулы,
содержащей
 атомов (
= 1, 2
и более)? Сформулируйте закон
равнораспределения энергии по степеням
свободы молекулы. Что называют внутренней
энергией и чему равна внутренняя энергия
идеального газа в зависимости от его
количества, числа атомов в молекул и
характера их движения?
атомов (
= 1, 2
и более)? Сформулируйте закон
равнораспределения энергии по степеням
свободы молекулы. Что называют внутренней
энергией и чему равна внутренняя энергия
идеального газа в зависимости от его
количества, числа атомов в молекул и
характера их движения?
Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы. Если материальная точка свободно движется в пространстве, то, как уже было сказано, она обладает тремя степенями свободы (координаты х, у и z), если она движется по некоторой поверхности, то двумя степенями свободы, если вдоль некоторой линии, то одной степенью свободы.
Закон
Больцмана о равномерном распределении
энергии по степеням свободы молекул:
для статистической системы, находящейся
в состоянии термодинамического
равновесия, на каждую поступательную
и вращательную степени свободы приходится
в среднем кинетическая энергия, равная
kT/2,
а на каждую колебательную степень
свободы — в среднем энергия, равная kT.
Колебательная степень «обладает» вдвое
большей энергией потому, что на нее
приходится не только кинетическая
энергия (как в случае поступательного
и вращательного движений), но и
потенциальная, причем средние значения
кинетической и потенциальной энергий
одинаковы. Таким образом, средняя энергия
молекулы
![]() где
i
— сумма числа поступательных, числа
вращательных в удвоенного числа
колебательных степеней свободы
молекулы:
где
i
— сумма числа поступательных, числа
вращательных в удвоенного числа
колебательных степеней свободы
молекулы:![]() В классической теории рассматривают
молекулы с жесткой связью между атомами;
для них i совпадает с числом степеней
свободы молекулы. Так как в идеальном
газе взаимная потенциальная энергия
молекул равна нулю (молекулы между собой
не взаимодействуют), то внутренняя
энергия, отнесенная к одному молю газа,
будет равна сумме кинетических энергий
Na
молекул:
В классической теории рассматривают
молекулы с жесткой связью между атомами;
для них i совпадает с числом степеней
свободы молекулы. Так как в идеальном
газе взаимная потенциальная энергия
молекул равна нулю (молекулы между собой
не взаимодействуют), то внутренняя
энергия, отнесенная к одному молю газа,
будет равна сумме кинетических энергий
Na
молекул:
![]() (50.1). Внутренняя энергия для произвольной
массы т газа.
(50.1). Внутренняя энергия для произвольной
массы т газа.
![]()
Внутренняя энергия — однозначная функция термодинамического состояния системы, т. е. в каждом состоянии система обладает вполне определенной внутренней энергией (она не зависит от того, как система пришла в данное состояние). Это означает, что при переходе системы из одного состояния в другое изменение внутренней энергии определяется только разностью значений внутренней энергии этих состояний и не зависит от пути перехода.
