
- •1.Масса.Сила.Импульс тела и импульс силы. Закон сохранения и изменения импульса.
- •2.Центр инерции. Закон движения центра масс.
- •3.Движение тела в переменной массой . Выведение уравнения Мещерского
- •4.24.Консервативные силы. Потенциальная энергия. Связь между потенц. Энергией и силой.
- •5. Какое силовое поле называют потенциальным? Докажите, что однородное и центральное силовые поля являются потенциальными. Как определяется сила через потенциальную энергию?
- •6. Что называют механической энергией? Сформулируйте закон ее сохранения. Дайте определение кинетической и потенциальной энергий и выведите закон сохранения энергии в механике.
- •7.Механическая работа. Мощность. Кинетическая и потенциальная энергия тела. Закон сохранения и изменения механической энергии.
- •9.Сформулируйте постулаты специальной теории относительности. Запишите преобразования Лоренца для координат и времени. Как связаны длины и промежутки времени в разных системах отсчета?
- •10. Сформулируйте постулаты специальной теории относительности. Дайте определение интервала между событиями и докажите его инвариантность относительно преобразований Лоренца.
- •11. Запишите преобразования Лоренца для координат и времени. Выведите из них закон сложения скоростей в релятивистской механике.
- •12. Как рассчитывается кинетическая энергия релятивистской частицы, полная энергия и энергия покоя. Взаимосвязь полной энергии и импульса.
- •13. Уравнение движения тела в неинерциальных системах отсчета. Что такое силы инерции? Классифицируйте силы инерции по характеру движения неинерциальной системы отсчета и тела в ней.
- •14. Момент инерции. Вывести формулу для момента инерции сплошного диска относительно оси симметрии. Теорема Штейнера, ее вывод.
- •15. Момент инерции тела относительно оси. Доказательство теоремы Штейнера. Моменты инерции однородных тел (стержня, цилиндра, шара) относительно осей симметрии.
- •17. Что называют моментом импульса системы относительно данной точки? Выведите закон изменения момента импульса системы частиц. Сформулируйте закон сохранения момента импульса.
- •18. Пружинный маятник. Выведите дифференциальное уравнение его свободных незатухающих колебаний и запишите его решение.
- •19. Математический и пружинный маятники. Вывод формулы для расчета периодов их свободных незатухающих колебаний.
- •20. Физический маятник. Его приведенная длина. Вывод формулы для расчета периода его свободных незатухающих колебаний.
- •26. Выведите дифференциальное уравнение затухающих гармонических колебаний и запишите его решение. Дайте определение логарифмического декремента затухания.
- •27. Какие колебания называют вынужденными? Запишите дифференциальное уравнение вынужденных колебаний и его решение. Резонанс. Выведите формулу для расчета резонансной частоты.
- •29. Что такое волна? Уравнение бегущей плоской гармонической волны.
- •32. Получите уравнение стоячей волны. Пучности и узлы, условия их расположения.
- •33. Что такое волна? Уравнение плоской бегущей гармонической волны. В чем состоит эффект Доплера? Выведите формулу для частоты волны при движении ее источника и приемника.
- •36. Выведите барометрическую формулу. Получите из нее закон Больцмана для распределения частиц во внешнем силовом потенциальном поле.
- •38. Теплоемкость тела. Удельная и молярная теплоемкость, связь между ними. Классическая теория теплоемкости идеального газа и ее недостатки.
- •39. Объясните явление теплопроводности. Выведите закон Фурье. Поясните физический смысл коэффициента теплопроводности.
- •40. Объясните явление диффузии. Выведите закон Фика. Поясните физический смысл коэффициента диффузии.
- •41. Явления переноса. Выведите закон Фика. Получите выражение для коэффициента диффузии через усредненные характеристики теплового движения молекул.
- •42. Объясните явление вязкости. Выведите формулу Ньютона для силы вязкого трения. Объясните физический смысл коэффициента вязкости.
- •43. Адиабатный процесс. Вывод закона Пуассона. Работа газа в адиабатном процессе.
- •46. Энтропия. Определение энтропии через термодинамическую вероятность. Приведите различные формулировки второго закона термодинамики.
- •47. Приведите различные формулировки второго закона термодинамики. Теорема Нернста.
- •48.49. Реальные газы. Сила и потенциальная энергия межмолекулярного взаимодействия. Уравнение и изотермы Ван-дер-Ваальса.
- •50. Фаза, фазовые переходы между агрегатными состояниями вещества. Фазовые переходы 1 и 2 рода.
32. Получите уравнение стоячей волны. Пучности и узлы, условия их расположения.
Для
вывода уравнения стоячей волны
предположим, что две плоские волны
распространяются навстречу друг
другу вдоль оси х в среде без затухания,
причем обе волны характеризуются
одинаковыми амплитудами и частотами.
Кроме того, начало координат выберем в
точке, в которой обе волны имеют одинаковую
начальную фазу, а отсчет времени начнем
с момента, когда начальные фазы обеих
волн равны нулю. Тогда соответственно
уравнения волны, распространяющейся
вдоль положительного направления оси
х, и волны, распространяющейся ей
навстречу, будут иметь вид
![]() (157.1). Сложив эти уравнения и учитывая,
что k=2v/X
получим уравнение стоячей волны:
(157.1). Сложив эти уравнения и учитывая,
что k=2v/X
получим уравнение стоячей волны:![]() (157.2)
(157.2)
Из уравнения стоячей волны (157.2) вытекает, что в каждой точке этой волны происходят колебания той же частоты с амплитудой Aст=|2А cos (2х/)|, зависящей от координаты х рассматриваемой точки.
В
точках среды, где
![]() (157.3) амплитуда колебаний достигает
максимального значения, равного 2А. В
точках среды, где
(157.3) амплитуда колебаний достигает
максимального значения, равного 2А. В
точках среды, где
![]() (157.4)
(157.4)
амплитуда колебаний обращается в нуль. Точки, в которых амплитуда колебаний максимальна (Аст=2А), называются пучностями стоячей волны, а точки, в которых амплитуда колебаний равна нулю (Aст=0), называются узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. Из выражений (157.3) и (157.4) получим соответственно координаты пучностей и узлов:
![]() (157.5);
(157.5);
![]() (157.6)
(157.6)
Из формул (157.5) и (157.6) следует, что расстояния между двумя соседними пучностями и двумя соседними узлами одинаковы и равны /2. Расстояние между соседними пучностью и узлом стоячей волны равно /4.
33. Что такое волна? Уравнение плоской бегущей гармонической волны. В чем состоит эффект Доплера? Выведите формулу для частоты волны при движении ее источника и приемника.
Волна — это явление распространения в пространстве с течением времени возмущения физической величины. Уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид ;
(154.4). Уравнение волны, распространяющейся вдоль отрицательного направления оси х, отличается от (154.4) только знаком члена kx. Основываясь на формуле Эйлера (140.7), уравнение плоской волны можно записать в виде
Эффектом Доплера называется изменение частоты колебаний, воспринимаемой приемником, при движении источника этих колебаний и приемника друг относительно друга. Например, из опыта известно, что тон гудка поезда повышается по мере его приближения к платформе и понижается при удалении, т. е. движение источника колебаний (гудка) относительно приемника (уха) изменяет частоту принимаемых колебаний. Для рассмотрения эффекта Доплера предположим, что источник и приемник звука движутся вдоль соединяющей их прямой; vист и vпр — соответственно скорости движения источника и приемника, причем они положительны, если источник (приемник) приближается к приемнику (источнику), и отрицательны, если удаляется. Частота колебаний источника равна v0.
1.
Источник и приемник покоятся относительно
среды, т. е.
vист
= vпр=0.
Если v
— скорость распространения звуковой
волны в рассматриваемой среда, то длина
волны =vT=v/v0.
Распространяясь в среде, волна достигнет
приемника и вызовет колебания его
звукочувствительного элемента с частотой
![]() .
Следовательно, частота v звука, которую
зарегистрирует приемник, равна частоте
v0,
с которой
звуковая волна излучается источником.
.
Следовательно, частота v звука, которую
зарегистрирует приемник, равна частоте
v0,
с которой
звуковая волна излучается источником.
2.
Приемник приближается к источнику, а
источник покоится,
т. е. vпр>0,
vист=0.
В данном случае скорость распространения
волны относительно приемника станет
равной v + vпр.
Так как длина волны при этом не меняется,
то
![]() т.
е. частота колебаний, воспринимаемых
приемником, в (v+vпр)/v
раз больше частоты колебаний источника.
т.
е. частота колебаний, воспринимаемых
приемником, в (v+vпр)/v
раз больше частоты колебаний источника.
3. Источник приближается к преемнику, а приемник покоится, т. е. vист >0, vпр=0.
Скорость
распространения колебаний зависит лишь
от свойств среды, поэтому за время,
равное периоду колебаний источника,
излученная им волна пройдет в направлении
к приемнику расстояние vT
(равное длине волны )
независимо от того, движется ли источник
или покоится. За это же время источник
пройдет в направлении волны расстояние
vистT
, т. е. длина волны в направлении движения
сократится и станет равной
'=—vистТ=(v—vист)T,
тогда![]() ,
т. е. частота
колебаний, воспринимаемых приемником,
увеличится в v/(v
– vист)
раз. В случаях 2 и 3, если vист<0
и vпр<0,
знак будет обратным.
,
т. е. частота
колебаний, воспринимаемых приемником,
увеличится в v/(v
– vист)
раз. В случаях 2 и 3, если vист<0
и vпр<0,
знак будет обратным.
4.
Источник и приемник движутся относительно
друг друга.
Используя результаты, полученные для
случаев 2 и 3, можно записать выражение
для частоты колебаний, воспринимаемых
приемником:
![]() (159.1), причем верхний знак берется, если
при движении источника или приемника
происходит их сближение, нижний знак —
в случае их взаимного удаления.
(159.1), причем верхний знак берется, если
при движении источника или приемника
происходит их сближение, нижний знак —
в случае их взаимного удаления.
Из приведенных формул следует, что эффект Доплера различен в зависимости от того, движется ли источник или приемник. Если направления скоростей vпр и vист не совпадают с проходящей через источник и приемник прямой, то вместо этих скоростей в формуле (159.1) надо брать их проекции на направление этой прямой.
34. Какой газ называют идеальным? Выведите основное уравнение молекулярно-кинетической теории идеального газа. Запишите его с использование различных термодинамических параметров. В чем состоит физический смысл температуры?
В идеальном газе силы взаимодействия между частицами (атомами, молекулами) пренебрежимо малы. К идеальному газу близки разреженные реальные газы при температурах, далёких от температуры их конденсации.
Вывод: одноатомный идеальный газ, молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие, выделим элементарную площадку S и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, движущаяся перпендикулярно площадке, передает ей импульс m0v – (– m0v) = 2m0v, где m0 — масса молекулы, v — ее скорость. За время t площадки S достигнут только те молекулы, которые заключены в объеме цилиндра с основанием S и высотой vt. Число этих молекул равно nSvt. Необходимо, однако, учитывать, что реально молекулы движутся к площадке S под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений. Число ударов молекул, движущихся в заданном направлении, о площадку S будет 1/6nSvt. При столкновении с площадкой эти молекулы передадут ей импульс
![]() Тогда
давление газа, оказываемое им на стенку
сосуда,
Тогда
давление газа, оказываемое им на стенку
сосуда,![]() (43.1). Если газ в объеме V содержит N молекул,
движущихся со скоростями v1,
v2,
..., vN,
то целесообразно рассматривать среднюю
квадратную скорость
(43.1). Если газ в объеме V содержит N молекул,
движущихся со скоростями v1,
v2,
..., vN,
то целесообразно рассматривать среднюю
квадратную скорость
![]() (43.2)
(43.2)
характеризующую всю совокупность молекул газа.
Уравнение
(43.1) с учетом (43.2) примет вид
![]() (43.3).
(43.3).
Выражение (43.3) называется основным уравнением молекулярно-кинетической теории идеальных газов.
Температура: Средняя кинетическая энергия поступательного движения одной молекулы идеального газа
![]() (43.8) пропорциональна
термодинамической температуре и
зависит только от нее. Из этого уравнения
следует, что при Т=0 <0>=0,
т. е. при 0К прекращается поступательное
движение молекул газа, а следовательно,
его давление равно нулю. Таким образом,
термодинамическая температура является
мерой средней кинетической энергии
поступательного движения молекул
идеального газа, и формула (43.8) раскрывает
молекулярно-кинетическое толкование
температуры.
(43.8) пропорциональна
термодинамической температуре и
зависит только от нее. Из этого уравнения
следует, что при Т=0 <0>=0,
т. е. при 0К прекращается поступательное
движение молекул газа, а следовательно,
его давление равно нулю. Таким образом,
термодинамическая температура является
мерой средней кинетической энергии
поступательного движения молекул
идеального газа, и формула (43.8) раскрывает
молекулярно-кинетическое толкование
температуры.
35. Изобразите на чертеже функцию распределения Максвелла по скоростям теплового движения молекул идеального газа. В чем состоит физический смысл этой функции? Запишите формулы для расчета наиболее вероятной, средней и среднеквадратичной скоростей молекул данного газа при данной температуре.
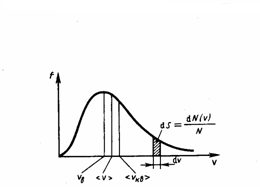 Закон о распределеня
молекул идеального газа по скоростям:
Закон о распределеня
молекул идеального газа по скоростям:
![]()
Физический смысл этой функции: функция показывает долю молекул, скорости которых находятся в данном единичном интервале скоростей, т.е. доля молекул в интервале скоростей (В данном единичном интервале скоростей число молекул среднестатистически остается постоянным с течением времени, т.е. состав молекул меняется, а количество молекул остается постоянно); к функции можно применить принцип детального равновесия.
Наиболее
вероятная скорость:
![]()
средняя
![]() средняя квадратичная
средняя квадратичная
![]() .
.
