5.3. Зависимость потерь напора от средней скорости течения в круглой цилиндрической трубе

При ламинарном режиме движения потери напора зависят от средней скорости течения линейно:

, (5.4)

а при турбулентном режиме – нелинейно:

, (5.5)

где 1,75≤m≤2; B_л и B_T - коэффициенты пропорциональности, зависящие от рода жидкости (её плотности ρ и вязкости μ), формы и размеров живого сечения. Коэффициент B_Т зависит еще и от шероховатости смоченной поверхности.

Х

Рис. 5.1

арактер зависимостей (5.4) и (5.5) показан на рис. 5.1. Ламинарному режиму отвечает прямая ОА. Точка А соответствует критической скорости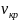 , т. е. переходу потока из ламинарного режима в турбулентный. От точки В и далее с увеличением скорости движение - турбулентное. Ему соответствует кривая ВС.

Коэффициенты B_л и B_Т, а также показатель m, определяют опытным путем, строя графики зависимостей (5.4) и (5.5) в логарифмических координатах (рис. 5.2). Логарифмирование (5.4) и (5.5) даёт:

Рис. 5.2

_и

.

Таким образом, в обоих выражениях связь между логарифмами h_l и - линейная. Но для ламинарного движения угловой коэффициент tgφ_л=1, а для турбулентного tgφ_Т=m.

Разный характер зависимостей h_l от средней скорости обусловлен различием кинематической структуры ламинарного и турбулентного потоков. Турбулентные пульсации скорости и давления порождают дополнительные касательные напряжения, которые вызывают повышенные потери энергии в турбулентных потоках по сравнению с ламинарными при сопоставимых условиях.

5.4. Основное уравнение равномерного движения в трубе

Рис. 5.3

Пусть в трубе жидкость движется равномерно со средней скоростью . Выделим сечениями 1-1 и 2-2 цилиндрический отсек радиусом r и длиной l (рис. 5.3). Уравнение динамического равновесия относительно оси движения S-S для выделенного отсека:

, (5.6)

где - сумма проекций внешних сил, - сумма проекций сил сопротивления на ось S-S. Определим силы, действующие на жидкость в отсеке:

1. Сила тяжести жидкости G=ρgωl, её проекция на ось S-S:

(5.7)

2. Силы давления на торцевые поверхности отсека: P₁=p₁ω и P₂=p₂ω. Сумма проекций этих сил на ось S-S

. (5.8)

3. Силы давления на боковую поверхность направлены перпендикулярно к оси движения S-S, поэтому проекции этих сил будут равны нулю.

4. Суммарная сила сопротивления (трения)

, (5.9)

где τ - сила сопротивления трения, приходящаяся на единицу боковой поверхности выделенного отсека (среднее касательное напряжение).

C учетом (5.7)-(5.9) уравнение (5.6) примет вид:

ρ·g·ω·(Z₁-Z₂)+(p₁-p₂)·ω=τ·l·χ. (5.10)

Разделив (5.10) на ρgω и преобразовав, получим

. (5.11)

Поскольку левая часть (5.11) представляет собой (при равномерном движении) потерю напора по длине , можно окончательно написать

(5.12)

или

, (5.13)

где - гидравлический или пьезометрический уклон (при равномерном движении эти уклоны равны).

Уравнение (5.13) - основное уравнение равномерного движения жидкости в цилиндрической трубе.