
- •Раздел 6
- •Повторение
- •1. Неопределенный интеграл
- •1.1. Первообразная функции. Неопределенный интеграл
- •1.2. Свойства неопределенного интеграла
- •1.3. Таблица основных неопределенных интегралов
- •2. Методы интегрирования
- •2.1. Метод непосредственного интегрирования
- •2.2. Метод интегрирования подстановкой (заменой переменной)
- •2.3. Метод интегрирования по частям
- •3. Интегрирование рациональных,
- •3.1. Понятия о рациональной функции
- •3.1.1. Многочлен
- •3.1.2. Дробно-рациональная функция
- •3.2. Интегрирование рациональных дробей
- •3.3. Интегрирование тригонометрических функций
- •3.3.1. Интегралы вида
- •3.3.2. Интегралы вида
- •3.4.2. Дробно-линейная подстановка
- •3.4.3. Тригонометрическая подстановка
- •3.4.4. Интегрирование дифференциального бинома
- •3.5. «Берущиеся» и «неберущиеся» интегралы
- •I. О технике интегрирования
- •II. Использование таблиц интегрирования
- •III. Об интегрировании в элементарных функциях
- •4. Определенный интеграл
- •4.1. Понятие определенного интеграла
- •Задача о площади криволинейной трапеции
- •Задача о работе переменой силы
- •4.2. Основные свойства определенного интеграла
- •4.3. Формула НьютонаЛейбница
- •4.4. Вычисление определенного интеграла
- •5. Несобственные интегралы
- •5.1. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл первого рода)
- •5.2. Интеграл от разрывной функции (несобственный интеграл второго рода)
4.2. Основные свойства определенного интеграла
Свойство 1. Если и функция интегрируема на отрезке , то
 .
.
Свойство 2. Если функции
![]() и
и
![]() интегрируемы на отрезке
,
тогда интегрируема на
их сумма. Интеграл суммы равен сумме
интегралов.
интегрируемы на отрезке
,
тогда интегрируема на
их сумма. Интеграл суммы равен сумме
интегралов.
 .
.
Доказательство.
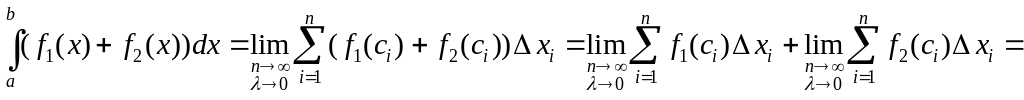
 .
.
Свойство 3.
 .
.
Свойство 4 (свойство аддитивности).
Если функция
интегрируема на отрезке
и
![]() ,
то интеграл по всему отрезку равен сумме
интегралов по частям этого отрезка:
,
то интеграл по всему отрезку равен сумме
интегралов по частям этого отрезка:
 ,
,
Свойство 5 (теорема о среднем). Если
функция
непрерывна на отрезке
,
то существует точка
![]() ,
такая, что справедливо равенство
,
такая, что справедливо равенство
 .
(4.3)
.
(4.3)
Доказательство. Пусть
.
Согласно теореме об ограниченности
непрерывной на отрезке
функции имеем
![]() ,
где
наименьшее значение
функции, а
наибольшее значение
функции на отрезке
.
,
где
наименьшее значение
функции, а
наибольшее значение
функции на отрезке
.
Очевидно, что если взять произвольное разбиение отрезка , то справедливы неравенства
 .
.
Перейдем к пределу в неравенствах, если . Тогда получаем
 .
.
Далее
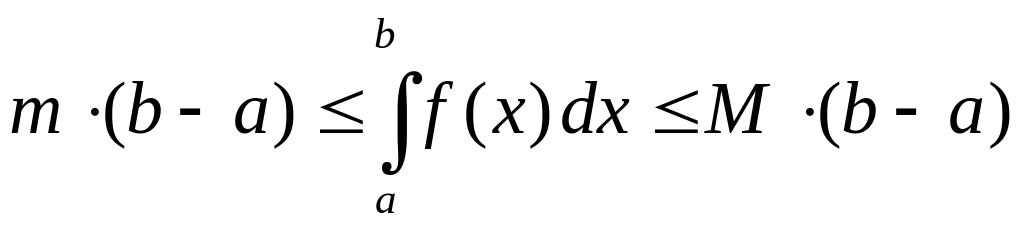 ,
,
откуда
 .
.
Непрерывная на отрезке функция принимает на нем все свои промежуточные значения между и . Поэтому найдется точка , такая, что
 ,
,
откуда следует формула (4.3).
Если
![]() ,
то
,
то
 .
.
Свойство 5 (теорема о среднем) при
![]() имеет простой геометрический смысл:
значение определенного интеграла, при
некотором
,
равно площади прямоугольника с высотой
имеет простой геометрический смысл:
значение определенного интеграла, при
некотором
,
равно площади прямоугольника с высотой
![]() и основанием
и основанием
![]() .
Число
.
Число

4.3. Формула НьютонаЛейбница
Пусть функция
непрерывна на отрезке
.
Тогда она интегрируема и на любом отрезке
![]() ,
где
,
где
![]() ,
т.е. для любого
,
т.е. для любого
![]() имеет смысл интеграл
имеет смысл интеграл
 .
Рассмотрим функцию
.
Рассмотрим функцию
 ,
(4.5)
,
(4.5)
которая определена на отрезке и называется интегралом с переменным верхним пределом.
Теорема 4.2. Если функция непрерывна на отрезке , то производная функции существует в каждой точке , причем
 .
.
Надо отметить, что любая функция , непрерывная на отрезке , имеет первообразную, определяемую формулой (4.5).
Теорема 4.3. Если функция непрерывна на отрезке и какая-нибудь первообразная для на этом отрезке, то справедлива формула НьютонаЛейбница
 .
(4.6)
.
(4.6)
Доказательство. Рассмотрим интеграл с переменным верхним пределом
 ,
,
где
,
на котором
непрерывна. Согласно теореме 4.2,
![]() .
.
Пусть первообразная функции , т.е. . Тогда по теореме 1.1 заключаем, что
![]() .
.
При получаем
 .
.
Далее
![]() ,
,
или
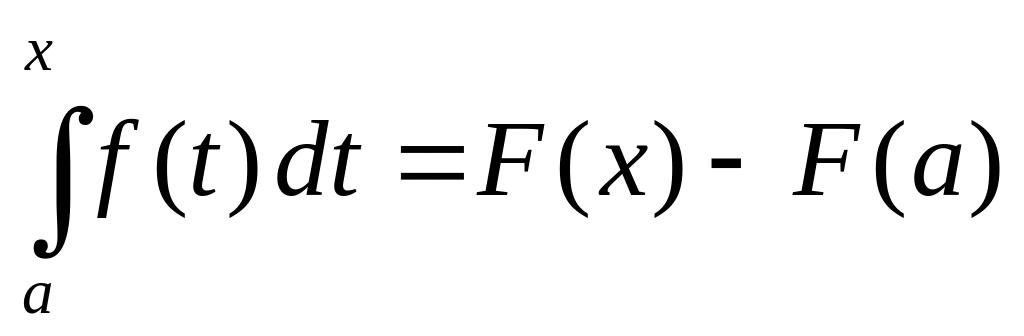 .
.
При получаем
 .
.
По свойству о независимости переменных получаем
.
Формулу НьютонаЛейбница (4.6) можно записать в виде
 ,
,
где
![]() называется двойной
подстановкой от
до
для функции
.
называется двойной
подстановкой от
до
для функции
.
Пример 4.1. Вычислить интеграл:
1)
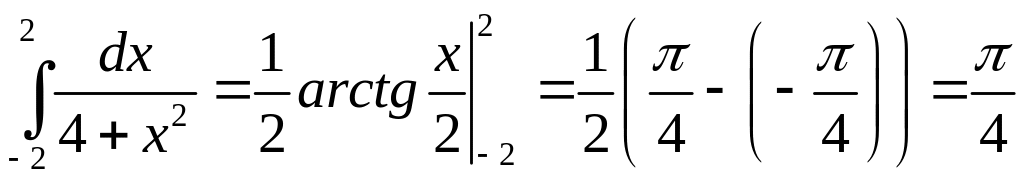 ;
;
2)
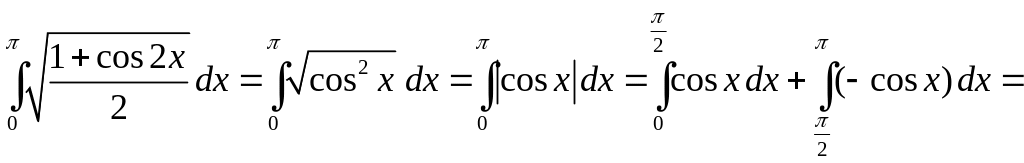
![]() .
.
4.4. Вычисление определенного интеграла
Простым и удобным методом вычисления определенного интеграла от непрерывной функции является формула НьютонаЛейбница. Кроме того, при вычислении определенного интеграла используются метод замены переменной и метод интегрирования по частям. Отметим только то, что:
1) не следует забывать менять пределы интегрирования при замене переменных;
2) при вычислении определенного интеграла методом постановки возвращаться к исходной переменной не требуется.
Рассмотрим на примерах, как используются эти методы при вычислении определенных интегралов.
Пример 4.2. Вычислить интеграл
 .
.
Решение. Способ 1.
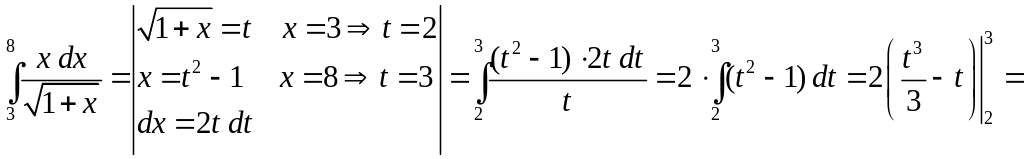
 .
.
Способ 2. Сначала найдем неопределенный интеграл
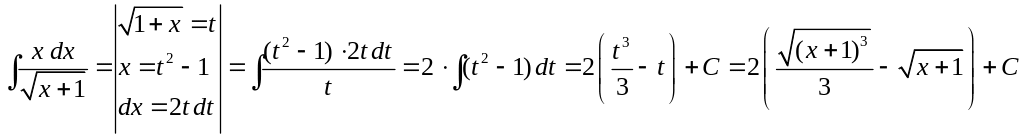
Далее находим определенный интеграл:
 .
.
Пример 4.3. Вычислить интеграл
 .
.
Решение.


![]() .
.
