3.3. Интегрирование тригонометрических функций

3.3.1. Интегралы вида

Рассмотрим некоторые случаи нахождения неопределенных интегралов от тригонометрических функций. Функции, содержащие и , над которыми выполняются рациональные операции (сложение, вычитание, умножение и деление) принято обозначать , где  знак рациональной функции.

Вычисление неопределенного интеграла вида сводится к вычислению интеграла от рациональной функции подстановкой , которая называется универсальной.

В этом случае:

, , , .

Поэтому

,

где рациональная функция от .

Пример 3.6. Найти следующие интегралы:

1) ;

2)

.



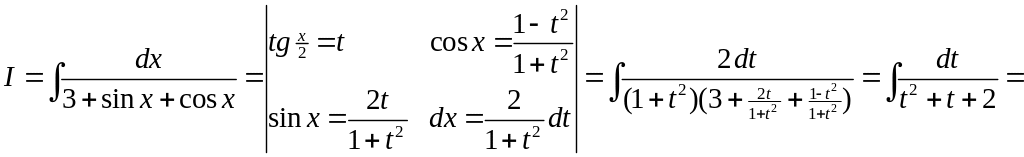
Универсальная подстановка часто приводит к довольно громоздким рациональным дробям и потому на практике применяется не очень часто. В некоторых случаях лучше применить другие подстановки. В частности удобны следующие правила:

1) если функция нечетная относительно , т.е. , то используется подстановка , которая рационализирует интеграл;

2) если функция нечетная относительно , т.е. , то используется подстановка ;

3) если функция четная относительно и , т.е. , то используется подстановка . Такая же подстановка применяется, если интеграл имеет вид .

Пример 3.7. Найти интеграл .

Решение.

. 

3.3.2. Интегралы вида

Для нахождения интегралов данного вида используются следующие приемы:

1) подстановка , если  целое положительное нечетное число;

2) подстановка , если  целое положительное нечетное число;

3) формулы понижения порядка: , , , если и  целые неотрицательные четные числа;

4) подстановка , если  есть четное отрицательное число.

Пример 3.8. Найти следующие интегралы:

1)

.

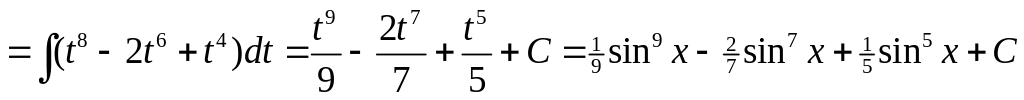2)

.

Надо отметить, что этот же интеграл можно найти, представив в виде и раскрыв в числителе скобки. 

3.3.3. Интегралы вида

Интегралы вида , и вычисляются с помощью следующих тригонометрических формул:

,

,

.

Пример 3.9. Найти интеграл .

Решение.



3.4. Интегрирование иррациональных функций

3.4.1. Интегралы иррациональных функций, содержащих

квадратный трехчлен в знаменателе

Рассмотрим некоторые виды интегралов, содержащих иррациональные функции.

Интегралы вида и называют неопределенными интегралами от квадратичных иррациональностей. Их можно найти следующим образом: под радикалом выделяется полный квадрат и делаем подстановку, в результате чего приходим к табличным интегралам.

Пример 3.10. Найти интегралы:

1)

.

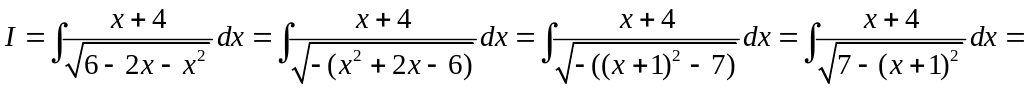
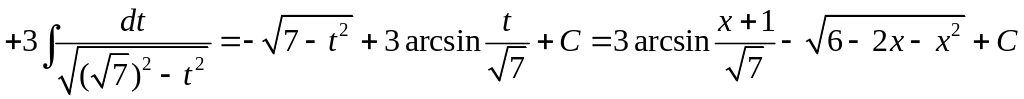2)

.



Интеграл вида можно вычислить, пользуясь формулой

,

где  многочлен степени ,  многочлен степени с неопределенными коэффициентами,   также неопределенный коэффициент.

Все неопределенные коэффициенты находятся из тождества, получаемого дифференцированием обеих частей равенства

,

после чего необходимо приравнять коэффициенты при одинаковых степенях неизвестной .

Интеграл вида целесообразно находить с помощью подстановки .