
- •Лабораторная работа №2 изучение законов фотоэффекта Задание №1. Проверка закона обратных квадратов
- •Задание №2. Изучение внешнего фотоэффекта, снятие вольтамперной характеристики электровакуумного фотоэлемента
- •Основные законы внешнего фотоэффекта
- •Задание №3. Определение красной границы фотоэффекта
Задание №3. Определение красной границы фотоэффекта
Приборы и принадлежности
Электровакуумный фотоэлемент; регулируемый источник питания с изменяемой полярностью; осветитель; два универсальных вольтметра; набор светофильтров (с указанными спектральными характеристиками); оптическая скамья.
Цель задания определение красной границы фото-эффекта.
Краткая теория
Закон Эйнштейна (5) непосредственно приводит к представлению о красной границе (пороге) фотоэффекта.
Для каждого металла должна существовать некоторая минимальная частота света v0, при которой ещё возможен вылет электронов. Эта минимальная частота v0 определяется из равенства
hv0 = A и = 0. (6)
Для частоты v = v0 энергия фотона такова, что может быть совершена работа выхода и вылетающий электрон покинет поверхность катода с начальной скоростью равной нулю.
Для кванта энергии с частотой v < v0 , т.е. при hv < А, электроны проводимости не могут выйти из катода за счет энергии поглощенного кванта, так как этой энергии недостаточно для преодоления работы выхода, и фотоэффект не наблюдается. Частота, рассчитываемая по уравнению (6), даёт ту минимальную частоту, при которой возможен фотоэффект, т.е. определяет порог фотоэффекта и называется предельной, или граничной, частотой фотоэффекта. Длина волны 0, соответствующая предельной частоте v0 и определяемая по формуле
0 = hc /A, (7)
называется красной границей фотоэффекта. Величина 0 зависит от природы вещества, состояния поверхности катода и особенно от наличия плёнок адсорбированного газа. Для большинства веществ она лежит в ультрафиолетовой области спектра. Но у некоторых металлов с малой работой выхода (особенно у щелочных – Na, K, Rb, Cs) наблюдается фотоэффект при видимом свете и красная граница лежит в видимой и инфракрасной областях спектра.
Электроны,
вылетающие из катода фотоэлемента под
действием света, обладают определённой
кинетической энергией и, достигая анода,
создают в замкнутой цепи, составленной
из фотоэлемента и гальванометра, ток.
Если
между
анодом и катодом создать электрическое
поле, приложив разность потенциалов,
то можно затормозить электроны. Методом
задерживающего потенциала обычно
пользуются при измерении энергии
фотоэлектронов. Те
электроны,
кинетическая энергия которых удовлетворяет
условию
![]() ,
не могут достичь анода. Поэтому при
увеличении напряжения U
анодный ток падает, и при некотором
значении разности потенциалов (потенциал
запирания)
даже самые
быстрые фотоэлектроны не могут достичь
анода, и анодный ток в цепи прекращается.
,
не могут достичь анода. Поэтому при
увеличении напряжения U
анодный ток падает, и при некотором
значении разности потенциалов (потенциал
запирания)
даже самые
быстрые фотоэлектроны не могут достичь
анода, и анодный ток в цепи прекращается.
Максимальная кинетическая энергия фотоэлектронов связана с задерживающим потенциалом соотношением (4).
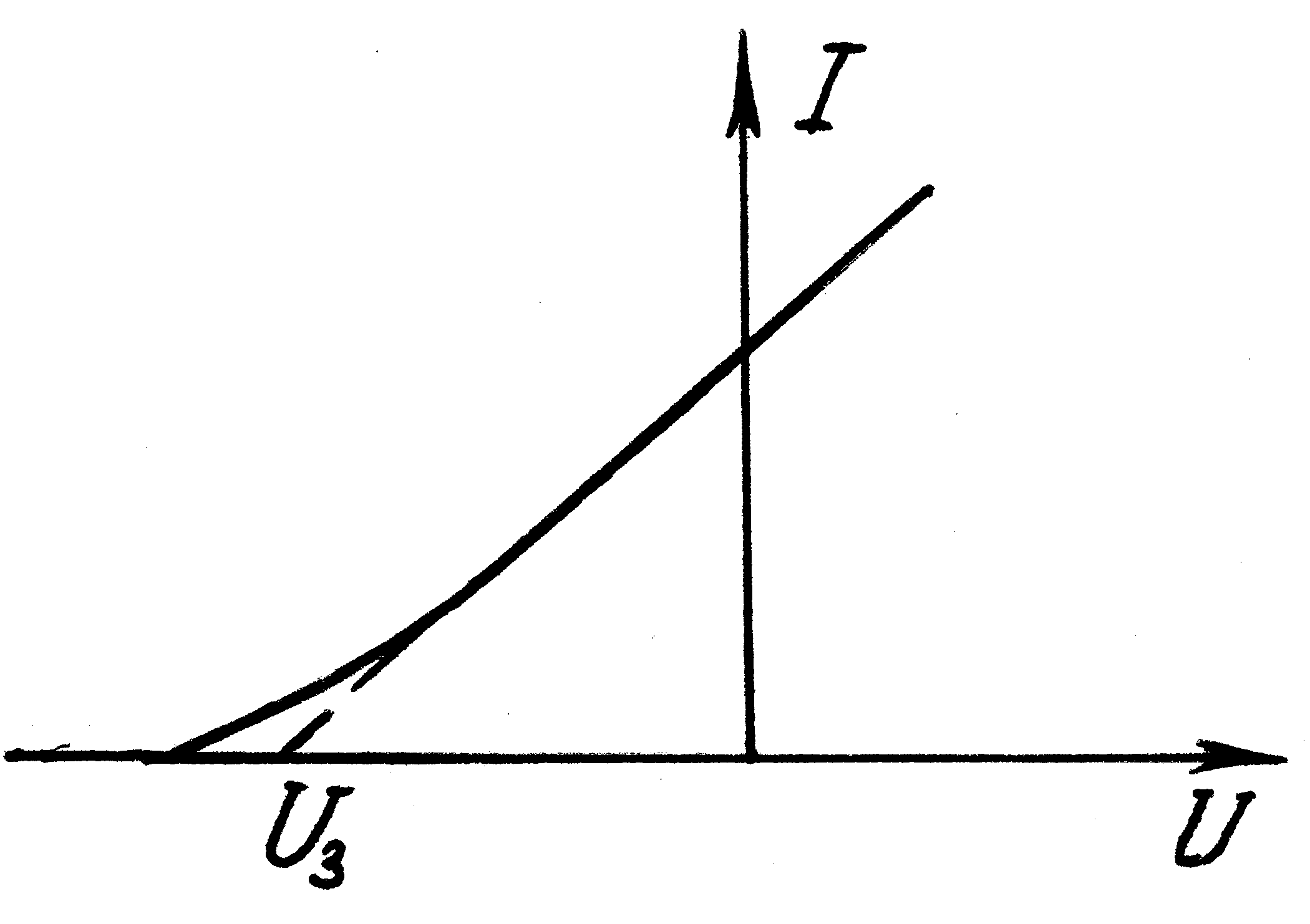
Рис. 6. Вольтамперная характеристика фотоэлемента при
запирающем напряжении
В задании № 3 экспериментально изучается зависимость фототока от величины приложенного задерживающего потенциала. Эта зависимость описывается плавной кривой, изображенной на рис. 6.
Практический интерес представляет точка пересечения кривой с осью U при I = 0, определяющая потенциал запирания UЗ (рис. 6)
UЗ = hv/e – A/e.
Это есть уравнение прямой линии, откуда видно, что задерживающий потенциал UЗ зависит от частоты света v, падающего на фотоэлемент.
При экспериментальной проверке уравнения Эйнштейна можно убедиться в том, что величина задерживающего потенциала зависит только от частоты света, причём линейно. Работу выхода электронов из металла и постоянную Планка можно определить, построив график зависимости задерживающего потенциала UЗ от частоты света v (рис. 7): tg= h/e, а отрезок b,
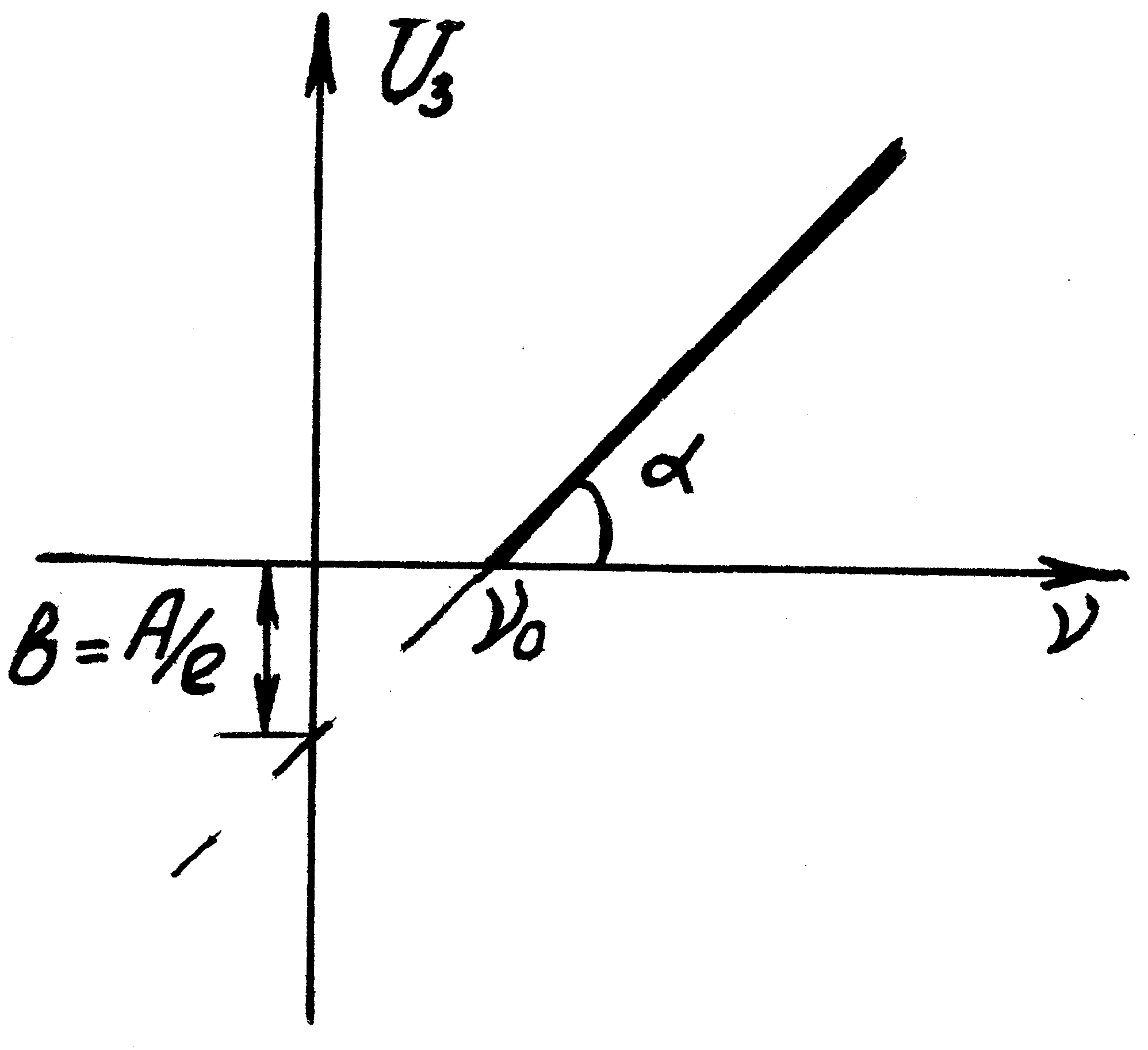
Рис. 7. Зависимость запирающего потенциала от частоты света
отсекаемый от оси потенциала, дает A/e. Точка пересечения прямой с осью абсцисс даёт численное значение граничной частоты v0. Иногда вместо частоты указывается длина волны 0 монохроматического света.
Если измерить величины задерживающего потенциала хотя бы для двух частот, то можно определить постоянную Планка и работу выхода электронов по формулам
h = (e/(v' – v'')) (UЗ' – UЗ"), (8)
А = (e/(v' – v")) (U3'v'' – U3" v'), (9)
где UЗ' и U3" задерживающие потенциалы для частот v' и v".
Порядок выполнения задания № 3
Для выполнения используется установка, описанная в задании № 2.
Включить источник питания и осветитель. Изменить полярность источника питания, подав на фотоэлемент запирающее напряжение
Снять вольтамперную характеристику при обратном напряжении, изменяя напряжение от 0 до U Uз.
Повторить п.2 минимум для трех различных светофильтров.
Построить кривые зависимости I от U для различных светофильтров и найти UЗ для каждого светофильтра.
Построить графики зависимости UЗ от v. Определить по расчетным формулам (8) и (9) графическим путём значения постоянной Планка, работы выхода и граничные частоты v0 (рис. 7).
Оценить точность измерений.
Контрольные вопросы к заданию № 3
Что понимают под красной границей фотоэффекта?
Каким уравнением определяется частота света при красной границе фотоэффекта?
Что понимают под термином задерживающее напряжение?
От чего зависит величина задерживающего потенци-ала?
Как связаны между собой граничная длина волны 0 и граничная частота v0?
Рекомендуемая литература
[5], [6], [9], [10], [11], [13], [14].
