Лазарева Т. Я., Мартемьянов Ю. Ф. Основы теории автоматического управления (2004)

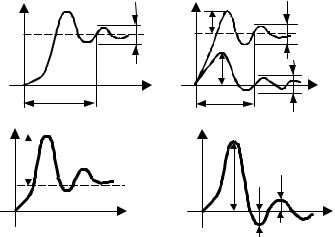
8.1.2 КОСВЕННЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА

Основную группу среди косвенных показателей качества составляют корневые показатели качества регулирования, к которым относятся степень устойчивости и степень колебательности. Эти показатели уже были использованы для определения оценки запаса устойчивости (п. 7.3, где было дано их определение). С точки зрения качества регулирования можно сделать следующие выводы.

1 Степень устойчивости, определяемая по формуле (7.7), характеризует интенсивность затухания наиболее медленно затухающей неколебательной составляющей переходного процесса, которая определяется как yк(t) = Скe–ηt. Пусть рассматриваемая система описывается дифференциальным уравнением второго порядка, характеристическое уравнение которого имеет два действительных различных корня s1 = – α1, s2 = – α2 и α1 < α2 (рис. 8.5, а). Последним соответствуют две элементарныесоставляющие свободного движения системы (рис. 8.5, б):

y1(t) = C1e−α1t ; y2 (t) = C2e−α2t .

Как видно из графиков переходных процессов, чем меньше абсолютное значение корня характеристического уравнения, тем медленнее затухает соответствующая ему составляющая. Результирующий переходный процесс y(t) = ∑yi (t) . Его затухание определяется наиболее медленно затухающей состав-

ляющей, т.е. наименьшим по абсолютному значению корнем характеристического уравнения.

ЕСЛИ ЖЕ ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ СИСТЕМЫ ИМЕЕТ КОМПЛЕКСНЫЕ СОПРЯЖЕННЫЕ КОРНИ, ТО СОСТАВЛЯЮЩАЯ ПЕРЕХОДНОГО ПРОЦЕССА YI(T) БУДЕТ ИМЕТЬ КОЛЕБАТЕЛЬНЫЙ ХАРАКТЕР YI(T) = СIЕ–ηTCOSωT, И ДЕЙСТВИТЕЛЬНАЯ ЧАСТЬ КОРНЯ, А ФАКТИЧЕСКИ СТЕПЕНЬ УСТОЙЧИВОСТИ, ТАК КАК η = α, ХАРАКТЕРИЗУЕТ

ОГИБАЮЩУЮ (РИС. 8.6).

РИС. 8.5 ОПРЕДЕЛЕНИЕ КАЧЕСТВА МОНОТОННЫХ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПО СТЕПЕНИ УСТОЙЧИВОСТИ:

А– РАСПОЛОЖЕНИЕ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ;

Б– СОСТАВЛЯЮЩИЕ ПЕРЕХОДНОГО ПРОЦЕССА

Рис. 8.6 Определение качества колебательных переходных процессов по степени устойчивости:

А– РАСПОЛОЖЕНИЕ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ;

Б– ПЕРЕХОДНЫЕ ПРОЦЕССЫ

Как видно из рис. 8.6, два колебательных переходных процесса разной частоты имеют одинаковые огибающие, т.е. yогиб = e–ηt. Но при одинаковой степени устойчивости качество этих пере-

ходных процессов существенно отличается друг от друга. Следовательно, знания степени устойчивости для оценки качества колебательных переходных процессов недостаточно.

Степень устойчивости может быть использована для оценки времени регулирования монотонных переходных процессов. Касательная к Cy = e–ηt в точке t = 0 отсекает на оси абсцисс отрезок η1 (рис. 8.5, б). Время регулирования в этом случае определяется как

Если требуется уменьшить время регулирования, то, как следует из (8.3), степень устойчивости надо увеличивать. При оценке времени регулирования частота не учитывается.

2 Степень колебательности так же, как и степень устойчивости, используется и для оценки запаса устойчивости и для оценки качества регулирования. Степень колебательности, определяемая в соответствии с (7.8), характеризует затухание наиболее медленно затухающей составляющей, которая определяется какy(t) = Ae–mωtsinωt, откуда следует, что изменение частоты влечет иизменение амплитуды колебаний.

Степень колебательности однозначно связана со степенью затухания. Действительно, в момент времени t0 амплитуда свободной составляющей определяется как у1= Ae−mωt0 , а в момент времени t0 +

Степень затухания изменяется от 0 до 1, а степень колебательности – от 0 до ∞. Наиболее часто используются следующие их значения: m = 0,141 (ψ = 0,61); m = 0,221 (ψ = 0,75); m = 0,366 (ψ =

где Wз.с(s) – передаточная функция замкнутой системы по каналу ошибки; X(s) – изображение задающего воздействия, в большинстве случаев x(t) = С = const и тогда X(s) = Cs . С учетом вышесказанного

Из последнего соотношения видно, что в системах с П-регулятором статическая ошибка уменьшается с увеличением значения параметра настройки регулятора. В реальных системах берется максимально возможное значение S1, исходя из обеспечения запаса устойчивости.

Взаключение следует заметить, что динамическая ошибка корневыми методами не оценивается.

8.1.3ИНТЕГРАЛЬНЫЕ КРИТЕРИИ КАЧЕСТВА

Интегральные критерии качества представляют собой определенные интегралы по времени в пределах от 0 до ∞ от некоторой функции переходного процесса y(t) или ошибки ε(t) и вычисляются непосредственно, либо по переходным функциям системы, или по коэффициентам передаточной функции системы. Целью использования этих критериев является получение общей оценки быстродействия и отклонения регулируемой величины от установившегося значения. К интегральным критериям качества предъявляются два требования: а) простота вычисления интеграла; б) несложность выражения через коэффициенты дифференциального уравнения.

8.1.3.1 Линейный интегральный критерий

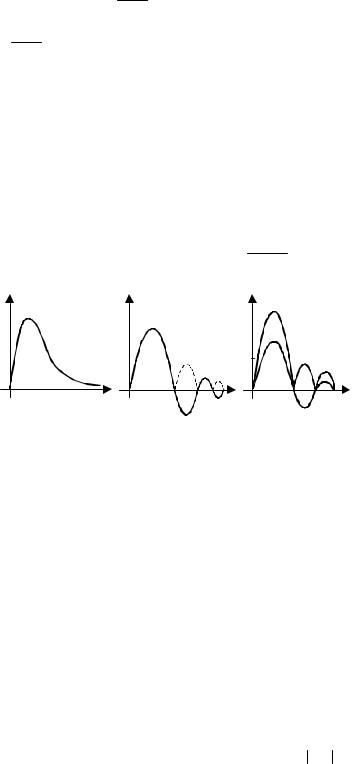
служит для оценки качества неколебательных процессов. Геометрически этот критерий характеризует площадь, заключенную между кривой переходного процесса и осью абсцисс (рис. 8.7, а), он учитывает как время регулирования, так и величину динамических отклонений. Если неизвестна кривая переходного процесса, но известна передаточная функция замкнутой системы Wз.с(s) и входная переменная x(t) = 1(t), то значение линейного интегрального критерия определяется с использованием теоремы о конечном значении функции. Действительно, формулу (8.6) можно записать иначе:

t

Jл = lim ∫y(τ)dτ

t→∞ 0

и тогда

Линейный интегральный критерий качества можно вычислить и другими методами. Например, если даны дифференциальное уравнение и начальные условия:

an y(n)(t) + an – 1 y (n – 1)(t) + ... + a0y(t) = 0,

y(n – 1)(0), ..., y ′(0), y(0),

то, проинтегрировав его, получим

Jл = an y(n−1) (0) + an−1y(n−2) (0) + ... + a1y(0) , a0

а при нулевых начальных условиях

Jл = a1y(0) . a0

Существуют модификации линейного интегрального критерия, которые применяются в тех случаях, когда начальный участок переходного процесса является менее ответственным, например,

∞

J л = ∫ty(t)dt ..

0

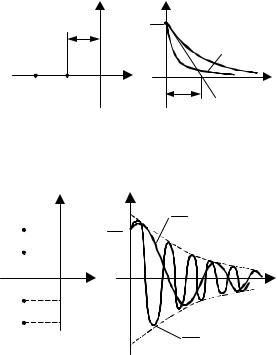
Выведем формулу, позволяющую вычислять такой критерий. Для этого продифференцируем по s функцию

∞

y(s) = ∫ y(t)e−st dt ,

0

осуществляющую преобразование по Лапласу функции y(t):

∞

dyds(s) = −∫ty(t)e−st dt .

0

Если перейти к пределу dyds(s) при s → 0, то получим

Jл* = lim(−1)y′(s) .

s→0

Следует отметить, что для вычисления таких критериев не требуется знание переходного процесса. Чем меньше значение линейного интегрального критерия, тем лучше качество процесса регулирования. Однако использование данного типа критериев для знакопеременных переходных процессов не дает объективной картины, так, например, для незатухающей синусоиды Jл = 0. Поэтому для оценки качества регулирования таких процессов используют ин-тегральные оценки, знакопеременность подынтегральной функции которых устранена каким-либо способом.

применяется для оценки качества колебательных процессов, а для неколебательных процессов он совпадает с линейным интегральным критерием. Для его вычисления требуется знание переходного процесса. На практике этот критерий используется при численном исследовании систем на моделях с применением вычислительной техники, т.е. там, где операция взятия модуля не представляет трудности. Геометрически критерий равен площади, заключенной между кривой y(t) и осью абсцисс (рис. 8.7, б).

В некоторых случаях используют модификацию модульного интегрального критерия:

котораяпридаетбольший вес значениям переходного процессавегоконце.

8.1.3.3 Интегральный квадратичный критерий

является наиболее распространенным критерием качества и представляет собой площадь под кривой y2(t) (рис. 8.7, в). Как видно из (8.9), разные по величине ординаты переходного процесса входят в критерий с разным весом, что приводит к тому, что начальный участок переходного процесса приобретает наибольшее значение, чем его "хвост", который практически не влияет на квадратичный критерий. Стремясь минимизировать (8.9), фактически минимизируют наибольшие отклонения регулируемой величины, поэтому минимальные значения критерия всегда соответствуют колебательным процессам с малым затуханием. С целью устранения этого недостатка применяют улучшенную квадратичную оценку:

которая, кроме самих отклонений, учитывает с весовым коэффициентом их производную. Весовой коэффициент выбирается равным желаемому времени нарастания или применяется в пределах

где Тр – желаемая длительность переходного процесса.

Квадратичный критерий, как и линейный, можно вычислить без построения переходного процесса по частотной характеристике замкнутой системы и преобразованию по Фурье от входного сигнала.

Используя формулу Релея, получают:

В заключение следует отметить, что абсолютные значения любой интегральной оценки сами по себе не представляют интереса. Они служат для сопоставления различных вариантов настройки одной и той же системы, а также для определения параметров настройки системы.

8.2Частотные методы анализа качества регулирования

Винженерной практике широко используются частотные методы исследования систем управления. В частности, группа методов, разработанная В. В. Солодовниковым, позволяет оценить качество регулирования по вещественным частотным характеристикам, построить переходные процессы, а также

синтезировать корректирующие устройства.

8.2.1ЗАВИСИМОСТЬ МЕЖДУ ПЕРЕХОДНОЙ И ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ

ДЛЯ ОЦЕНКИ КАЧЕСТВА РЕГУЛИРОВАНИЯ НЕОБХОДИМО УСТАНОВИТЬ СВЯЗЬ МЕЖДУ ПЕРЕХОДНОЙ И ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ. В ЧАСТОТНОЙ ОБЛАСТИ ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА ЗАПИСЫВАЕТСЯ ЧЕРЕЗ ПРЕОБРАЗОВАНИЕ ФУРЬЕ:

0

и через АФХ системы и изображение входной переменной по Фурье, с другой стороны

Используя обратное преобразование Фурье и последние соотношения, переходный процесс (переходная характеристика) определяется следующим образом:

На практике используется формула (8.14), в которой ВЧХ представляет собой сложную функцию и интегрирование возможно только приближенно: численными методами с применением ЭВМ либо путем предварительной аппроксимации сложной характеристики Re(ω) кусочно-линейнымифунк- циямисуммой трапеций илисуммой треугольников, чтопозволяетполучить достаточно удобные выражения.

Если на систему действует произвольное возмущение, то переходный процесс определяется по обобщенным вещественной и мнимой характеристикам:

Reоб(ω) = Re[W(iω) X (iω)], Imоб(ω) = Im[W(iω) X (iω)] , (8.16)

при этом необходимо, чтобы полюсы функции W(s) X(s) располагались слева от мнимой оси.

8.2.2 СВОЙСТВА ВЕЩЕСТВЕННО-ЧАСТОТНЫХ ХАРАКТЕРИСТИК И СООТВЕТСТВУЮЩИХ ИМ ПЕРЕХОДНЫХ ПРОЦЕССОВ

Основные свойства ВЧХ и переходных процессовследуютиз (8.14). 1 Свойство линейности: если ВЧХ можно представить суммой

j=1

2 Соответствие масштабов по оси ординат для Rе(ω) и у(t).

Еслиумножить Rе(ω) на постоянный множитель α, то соответствующее значение у(t) тоже умножается на этот множитель α (рис. 8.8).

3 Соответствие масштабов по оси абсцисс для Rе(ω) и у(t).

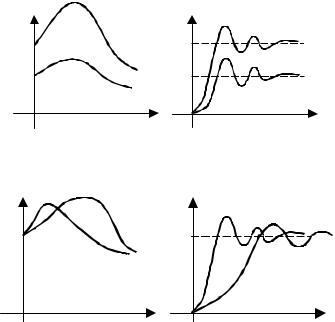
Если аргумент ω в соответствующем выражении частотной характеристики умножить на постоянное число, то аргумент в соответствующем выражении переходного процесса будет делиться на это число (рис. 8.9), т.е.

Рис. 8.9 Соответствие масштабов по оси абсцисс:

а – ВЧХ; б – переходные процессы

4 Начальное значение ВЧХ равно конечному значению переходной характеристики (рис. 8.9)

Начальное значение МЧХ Im(0) = 0.

5 Конечное значение ВЧХ равно начальному значению переходной характеристики

Интерес представляют разрывы непрерывности и пики в ве-щественно-частотной характеристике.

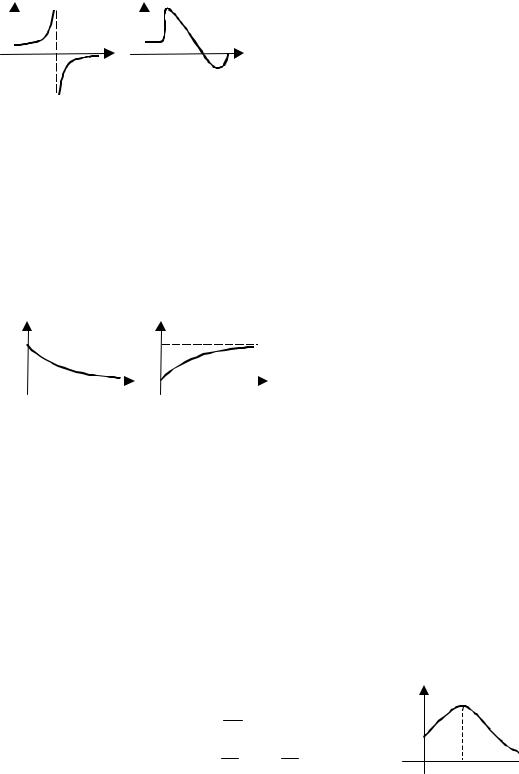
Пусть при ω = ω1 ВЧХ имеет разрыв непрерывности (рис. 8.10, а) Rе(ω1) = ∞, при этом характеристическое уравнение системы будет иметь мнимый корень s1 = ± iω1, т.е. в системе устанавливаются незатухающие гармонические колебания, если остальные корни левые.

Высокий и острый пик ВЧХ, за которым Rе(ω) переходит через нуль при частоте близкой к ω1, соответствует медленно затухающим колебаниям (рис. 8.10, б).

Влияния вариаций параметров системы на ее статические и динамические свойства называются параметрическими возмущениями, а возникающие при этом отклонения характеристик системы от расчетных значений – параметрическими погрешностями (ошибками).

Для оценки степени влияния разброса и изменения параметров системы используют понятие – чувствительность системы. Чувствительность – это свойство системы изменять свои выходные переменные и показатели качества при отклонении того или иного ее параметра от исходного или расчетного значения. Для обозначения противоположного свойства используется понятие "грубость" и системы, сохраняющие свои свойства при любых параметрических возмущениях, называются грубыми или робастными.

Количественными оценками чувствительности являются:

– функция чувствительности;

– коэффициент чувствительности.

Функцией чувствительности называется частная производная какой-либо динамической характеристики или какого-либо показателя по изменяющемуся (варьируемому) параметру ki. Например, для передаточной функции W(s, ki), зависящей от параметра ki, функция чувствительности определяется как

ДЛЯ ПЕРЕХОДНОЙ ФУНКЦИИ H(T, KI) ПО ОТНОШЕНИЮ К ПАРАМЕТРУ KI:

где ki0 – расчетное значение параметра ki.

На практике часто используют относительную функцию чувствительности, которая соответственно для (8.26), (8.27) запишется:

Так, для одноконтурной системы автоматического регулирования, состоящей из объекта Wоб(s) = k0WобА (s) и регулятора Wp(s), относительная функция чувствительности по отношению к параметру k0 определяется соотношением

С УЧЕТОМ (5.86) ОНО ПРЕОБРАЗУЕТСЯ К ВИДУ

которое означает, что чувствительность типовой системы регулирования к изменениям свойств объекта полностью определяется только передаточной функцией разомкнутой системы. Чем меньше значение функции чувстви-тельности, т.е. чем грубее система, тем меньше дополнительное откло-нение выходной переменной и, следовательно, лучше качество системы.

Если функция чувствительности выражается числом, то она называется коэффициентом чувствительности. С помощью коэффициента чувствительности оценивается чувствительность числовых показателей качества, например, показателя колебательности, перерегулирование. Оценка изменения

хода процесса по отношению к возмущению производится по формуле ∆у(t) = Vkg (t) ∆k.