
- •3. Понятие о статистическом наблюдении. Организационные формы, виды и способы статистического наблюдения.
- •4. Статистическая сводка, ее содержание и задачи, роль в обобщении финансово-экономической информации предприятия.
- •5. Метод статистической группировки, его задачи. Виды группировок и их применение в статистике.
- •7. Табличное и графическое представление статистических данных.
- •10. Понятие о вариации признака в статистической совокупности. Система показателей вариации. Применение в анализе финансово-экономической деятельности предприятий.
- •11. Виды дисперсий, правило сложения дисперсий, расчет на его основе коэффициента детерминации и эмпирического корреляционного отношения. Практическое использование.
- •24. Статистическое изучение наличия, состава и использования оборотных средств предприятия.
7. Табличное и графическое представление статистических данных.
Метод сводки и группировки даёт обобщение результатов исследования и представляет их в виде таблиц, позволяя анализировать полученные результаты. Таблицы – наиболее рациональная форма изложения. Подлежащие таблицы показывает о чём идёт речь в таблице, расположена слева и представляет собой содержание строк. Сказуемое расположено сверху и представляет собой содержание граф. Сказуемое показывает, какими признаками характеризуется подлежащие. Таблицы бывают перечневые (простые), групповые и комбинационные. В перечневой таблице несистематизированное перечисление в подлежащем изучаемых явлений. Если изучаемая явления систематизированы, т. е. сгруппированному по одному признаку, получим групповую статистическую таблицу. Комбинационные или комбинированные – таблицы, в которых в подлежащем дана группировка единиц в совокупности по 2 и более признакам взятых в комбинации. В таблицах должно быть заглавие, указаны единицы измерения именованных показателей, подсчитаны итоги. Заглавие таблицы – краткое пояснение основного содержания статистической сводки. Итоговый этап – построение графиков на основании таблиц. Графики – самая эффективная форма представления статистических данных с точки зрения их восприятия. Это условное наглядное изображение статистических величин и их соотношений при помощи геометрических линий и фигур. Для построения графиков используют систему координат: ось абсцисс – периоды, варианты; ось ординат – уровни, частоты. На оси координат наносят масштабы, необходимо правильно их выбрать, чтобы графики расположились в центре поля. Чаще всего это линейный график, непрерывная линия, характеризующая непрерывность процесса. Структура явления изображается в виде круговой и секторной диаграммы. В зависимости от применения геометрических знаков графики бывают: точечные, линейные, столбиковые, полосовые, круговые. Граф-й способ представл-я группир-к: гистограмма, полигон, кумуллятор. Групп-ка хар-ся рисунком в виде прямоуг-ков, высота прямоуг. опред. стат. показателем, к-й хар-ет группу.
8.
Абсолютные и относительные статистические
величины. Основные виды относительных
величин. Явления
общес-го развития имеют колич-ю
определенность. Стат-ка измеряет и
выражает ее с помощью колич-х категорий
так называемых статистических величин.
Колич-я определенность явлений выражается
в абсолютных и относительных показателях.
Абсолютные
– непосред-но регистрируемые знач-я
статис-го показателя (числен-ть, площадь,
валовый сбор, фонд з/п) Абсол. явл-ся
первичными.. Различают два вида абсолютных
величин: индивидуальные и суммарные.
Индивидуальные
- абсолютные
величины, хар-щие размеры признака у
отдельных единиц совокупности. Они
получаются непосредственно в процессе
стат-го наблюдения и фиксируются в
первичных учетных документах. Суммарные
абсолютные величины хар-ют итог-ю
величину признака по опред-й совокупности
объектов, охваченных стат-м наблюдением.
Они являются суммой кол-ва ед-ц изучаемой
совокупности (численность
совокупности)
или суммой значений варьирующего
признака всех единиц совокупности
(объем
варьирующего признака).
Абсолютные статистические величины
представляют собой именованные
числа, т.е.
имеют какую-либо единицу измерения. В
зависимости от сущности исследуемого
явления абсолютные величины выражаются
в натуральных,
стоимостных
и трудовых
единицах измерения. Натуральные
единицы
измерения в свою очередь могут быть
простыми (тонны, штуки, метры, литры) и
сложными, являющимися комбинацией
нескольких разноименных величин
(тонно-километры, киловатт-часы,
человеко-часы и т.д.). Стоимостные
единицы измерения используются для
выражения объема разнородной продукции
в стоимостной форме (рубли, доллары). В
трудовых
единицах измерения учитываются затраты
труда, трудоемкость. Относительная
величина
– получаются путем деления одной абсол-й
величины на др-ю (урожайность=вал.
сбор/площадь) Величина, с которой
производится сравнение (знаменатель
дроби) обычно называется базой
сравнения
или основанием.
В зависимости от выбора базы сравнения
относительный показатель может быть
представлен в различных долях единицы:
десятых, сотых (%), тысячных (промилле
![]() - десятая часть процента), десятитысячных
(продецимилле
- десятая часть процента), десятитысячных
(продецимилле
![]() - сотая часть процента). По своему
содержанию относительные величины
подразделяются на виды:
1) относительная
величина динамики (i)
рассчитывается как отношение уровня
признака в определенный период или
момент времени к уровню этого же признака
в предшествующий период или момент
времени, т.е. она хар-ет изменение уровня
какого-либо явления во времени.
Относительные величины динами наз-ют
темпами роста.
2) относительная
величина планового задания ( iпл.з
)
рассчитывается как отношение уровня,
запланированного на предстоящий период,
к уровню, фактически сложившемуся в
этом периоде. 3) относительная
величина выполнения плана ( iвып.пл
)
представляет собой отношение фактически
достигнутого в данном периоде уровня
к запланированному. Относительные
величины динамики, планового задания
и выполнения плана связаны соотношением:
- сотая часть процента). По своему
содержанию относительные величины
подразделяются на виды:
1) относительная
величина динамики (i)
рассчитывается как отношение уровня
признака в определенный период или
момент времени к уровню этого же признака
в предшествующий период или момент
времени, т.е. она хар-ет изменение уровня
какого-либо явления во времени.
Относительные величины динами наз-ют
темпами роста.
2) относительная
величина планового задания ( iпл.з
)
рассчитывается как отношение уровня,
запланированного на предстоящий период,
к уровню, фактически сложившемуся в
этом периоде. 3) относительная
величина выполнения плана ( iвып.пл
)
представляет собой отношение фактически
достигнутого в данном периоде уровня
к запланированному. Относительные
величины динамики, планового задания
и выполнения плана связаны соотношением:
![]() .
4) относительные
величины структуры
характеризуют состав изучаемых
совокупностей; рассчитываются как
отношение абсолютной величины каждого
из элементов совокупности к абсолютной
величине всей совокупности (части к
целому) и представляют собой удельный
вес части в целом в %. 5) относительными
величинами интенсивности
наз-ют показатели, хар-щие степень
распространения или уровень развития
того или иного явления в определенной
среде. 6) относительными
величинами координации
наз-ют показатели, характеризующие
соотношение отдельных частей целого
м/у собой. 7) относительными
величинами сравнения
наз-ют показатели, представляющие собой
частные от деления одноименных абсолютных
величин, хар-щих разные объекты,
относящихся к одному и тому же периоду
времени.
.
4) относительные
величины структуры
характеризуют состав изучаемых
совокупностей; рассчитываются как
отношение абсолютной величины каждого
из элементов совокупности к абсолютной
величине всей совокупности (части к
целому) и представляют собой удельный
вес части в целом в %. 5) относительными
величинами интенсивности
наз-ют показатели, хар-щие степень
распространения или уровень развития
того или иного явления в определенной
среде. 6) относительными
величинами координации
наз-ют показатели, характеризующие
соотношение отдельных частей целого
м/у собой. 7) относительными
величинами сравнения
наз-ют показатели, представляющие собой
частные от деления одноименных абсолютных
величин, хар-щих разные объекты,
относящихся к одному и тому же периоду
времени.
9.
Средняя, ее сущность и условия применения.
Виды и формы средних. Средние
величины
– это обобщающие показатели общ-ых
явл-й по одному колич-но варьирующему
признаку. Ср.
выражает типичное ед-ц совокупности.
Особ-ти ср.:
1) она хар-ет ту или иную совокупность в
целом; 2) в ней ср. погашаются отдельные
индивидуальные отклонения единиц по
изучаемому признаку; 3) ср. отражает
типичные черты и св-ва массы ед-ц; 4) в
сочетании с методом стат-х группировок
возникает возможность изучения
взаимосвязей между группировочными и
результативными признаками; 5) ср.
величина явл-ся базой для прогнозирования;
6) многие процессы изучаются только на
основании ср.; 7) ср. показывает колич-ное
различие и сходство двух совокупностей.
При расчете
ср.: 1) расчет
только однородных по кач-ву совокупностей,
для этого надо сочетать метод ср. и метод
группировок; 2) общее ср. необходимо
дополнять групповыми средними и
индивидуальными величинами; 3) для
расчета ср. нужна масса единиц (20-30); 4)
необходимо правильно выбирать единицу
совокупности ср. В каждом конкретном
случае применяется одна из ср. величин:
арифметическая,
гармоническая, геометрическая,
квадратическая, кубическая и
т.д. Все они - класс степенных
средних и объединяются общей формулой
(при различных значениях m):
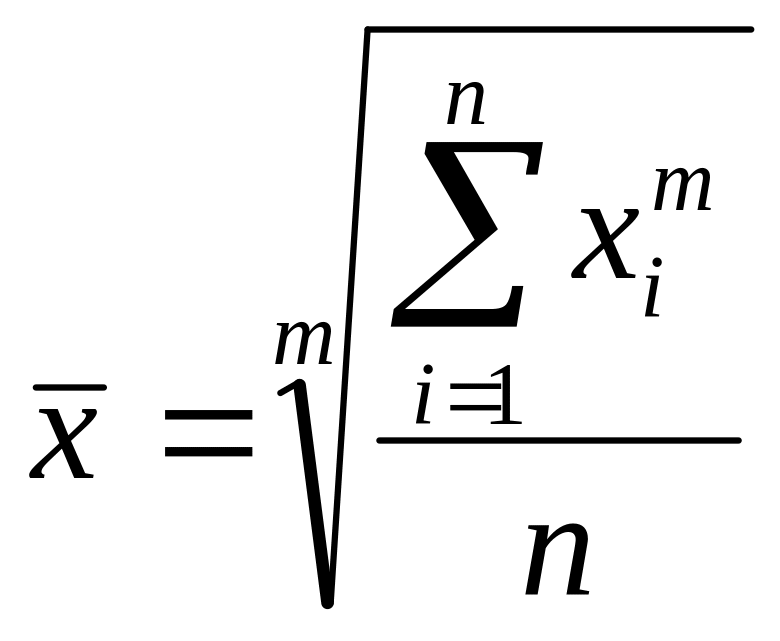 .
Различают следующие виды степенных
средних: 1)m
= -1 –
гармоническая
.
Различают следующие виды степенных
средних: 1)m
= -1 –
гармоническая
![]() ;
2)m
= 0 –
геометрическая
;
2)m
= 0 –
геометрическая
![]() ;
3)m
= 1 –
арифметическая
;
3)m
= 1 –
арифметическая
![]() ;
4) m
= 2 –
квадратическая
;
4) m
= 2 –
квадратическая
![]() ;
5) m
= 3 – ср.
кубическая
;
5) m
= 3 – ср.
кубическая
![]() .
Ср.
арифметическая:
наиболее распространенный вид средних.
Ср. арифметическая
применяется в форме простой
ср. и взвешенной
ср. Ср.
арифметическая простая
равна простой сумме отдельных значений
осредняемого признака, деленной на
общее число этих значений. Ср.
арифметическая взвешенная
– ср. сгруппированных величин х1,х2,…,хп
– вычисляется по формуле:
.
Ср.
арифметическая:
наиболее распространенный вид средних.
Ср. арифметическая
применяется в форме простой
ср. и взвешенной
ср. Ср.
арифметическая простая
равна простой сумме отдельных значений
осредняемого признака, деленной на
общее число этих значений. Ср.
арифметическая взвешенная
– ср. сгруппированных величин х1,х2,…,хп
– вычисляется по формуле:
![]() .
В отдельных случаях веса могут быть
представлены не абсолютными величинами,
а относительными (% или доли единиц).
Тогда формула ср.
арифметической взвешенной
будет иметь вид:
.
В отдельных случаях веса могут быть
представлены не абсолютными величинами,
а относительными (% или доли единиц).
Тогда формула ср.
арифметической взвешенной
будет иметь вид:
![]() ,
где
,
где
![]() -
частость, т.е. доля каждой частоты в
общей сумме всех частот. Если частоты
подсчитываются в долях
(коэффициентах), то
-
частость, т.е. доля каждой частоты в
общей сумме всех частот. Если частоты
подсчитываются в долях
(коэффициентах), то
![]() и формула средней арифметической
взвешенной имеет вид:
и формула средней арифметической
взвешенной имеет вид:
![]() .
Ср.
гармоническая:
когда стат-я информация не содержит
частот f
по отдельным вариантам х
совокупности, а представлена как их
произведение
.
Ср.
гармоническая:
когда стат-я информация не содержит
частот f
по отдельным вариантам х
совокупности, а представлена как их
произведение
![]() ,
применяется формула ср.
гармонической взвешенной:.
,
применяется формула ср.
гармонической взвешенной:.
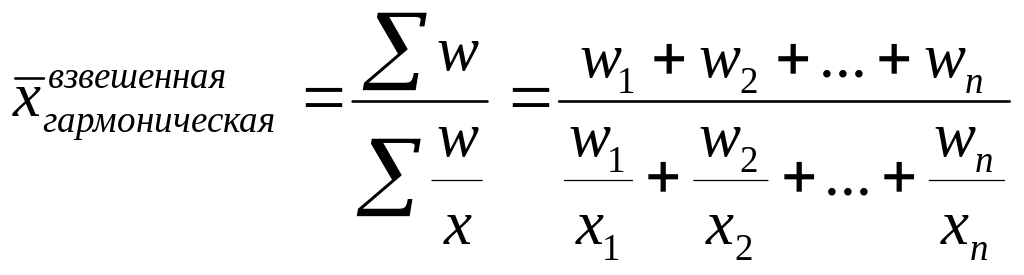
В
тех случаях, когда вес каждого варианта
равен 1 (индивидуальные знач-я обратного
признака встречаются по одному разу),
применяется ср.
гармоническая простая.
Ср.
геометрическая:
применяется, когда хар-ют средний коэфф-т
роста. Она исчисляется извлечением
корня степени п
из произведения отдельных значений.
Широко применяется для определения
средних темпов изменения в рядах
динамики, а также в рядах распределения.
Ср.
квадратическая:
применяется, когда нужен расчет среднего
размера признака, выраженного в квадратных
единицах измерения. Она бывает простой,
средней, кубической, кубической (простой,
взвешенной). Особым видом средних величин
являются структурные
ср. К таким
показателям относятся мода
и медиана.
Мода Мо
– значение случайной величины,
встречающееся с наибольшей вероятностью
в дискретном вариационном ряду –
вариант, имеющий наибольшую частоту.
Модальный интервал определяется по
наибольшей частоте. Медиана
Ме
– это вариант, к-й находится в середине
вариац-го ряда. Медиана делит ряд на две
равные части – меньше медианы и больше
медианы. Необходимо отыскать значение
признака, к-е находится в середине
упорядоченного ряда. В случае четного
объема ряда медиана равна средней из
двух вариантов. Значение медианы
вычисляется линейной интерполяцией по
формуле:
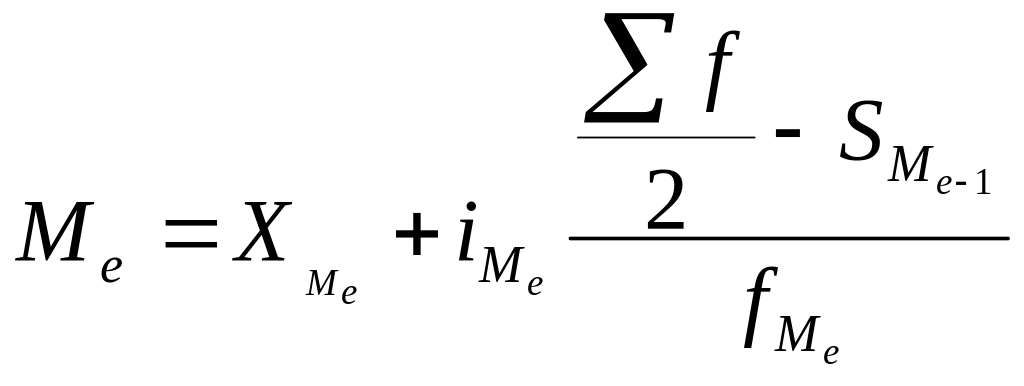 .
.
