1.4. Метод простой итерации

Пусть уравнение можно заменить эквивалентным ему уравнением

. (2)

Выберем каким-либо образом начальное приближение . Вычислим значение функции при и найдем уточненное значение . Подставим теперь в уравнение (1) и получим новое приближение и т. д. Продолжая этот процесс неограниченно, получим последовательность приближений к корню:

. (3)

Формула (3) является расчетной формулой метода простой итерации.

Если последовательность сходится при , т. е. существует

(4)

и функция непрерывна, то, переходя к пределу в (3) и учитывая (4), получим: .

Таким образом, , следовательно, – корень уравнения (2).

Сходимость метода. Сходимость метода простой итерации устанавливает следующая теорема.

Теорема. Пусть функция определена и диффе­ренцируема на отрезке , причем все ее зна­чения . Тогда, если выполняется условие при :

1) процесс итерации сходится независимо от начального значения ;

2) предельное значение является единственным корнем уравнения на отрезке .

Доказательство. Так как и , то можно записать

.

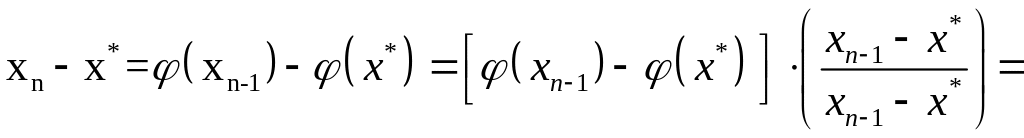
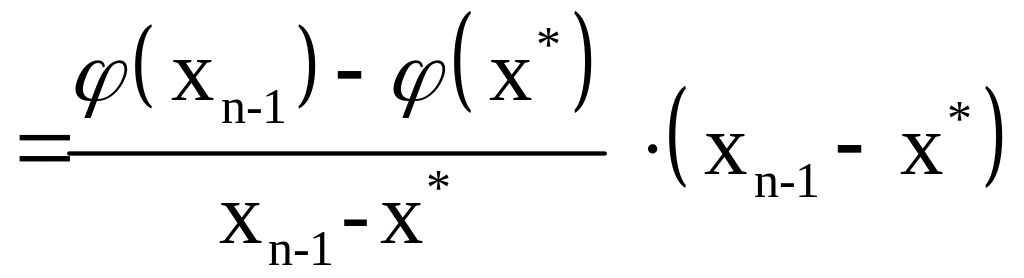По теореме о среднем (она утверждает, что если производная функции непрерывна на некотором интервале , то тангенс угла наклона хорды, проведенной между точками и , (т.е. равен производной функции в некоторой промежуточной точке, лежащей между и ) частное в последнем выражении будет равно , где – некоторая промежуточная точка в интервале поиска корня. Следовательно, .

Если ввести обозначение для всего интервала поиска, то предыдущее равенство может быть переписано в виде:

Аналогично . Тогда для будет справедливо неравенство: и т. д. Продолжая эти выкладки дальше, в результате получаем , где – натуральное число. Таким образом, чтобы метод сходился, необходимо выполнение неравенства: .

Отсюда следует, что должно быть меньше единицы. В свою очередь, для всех остальных значений меньших , можно записать: . Число определим из соотношения . Тогда справедливо неравенство (вывод см. ниже): . Если поставить условие, что истинное значение корня должно отличаться от приближенного значения на величину , т.е. , то приближения надо вычислять до тех пор, пока не будет выполнено неравенство

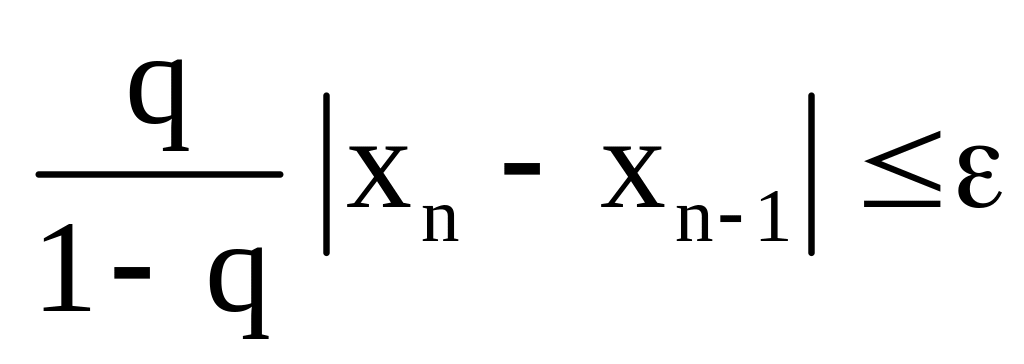или 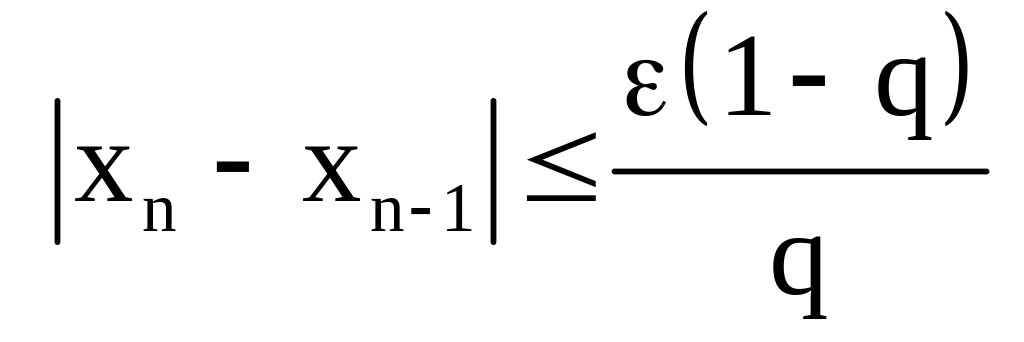и тогда .

Вывод неравенства. Рассмотрим два последовательных приближения: и . Отсюда .

Используя теорему о среднем, получим:

,

тогда на основании условия можно записать:

.

С другой стороны, пусть . Очевидно, что . Отсюда, учитывая, что , получим

,

где .

Тогда 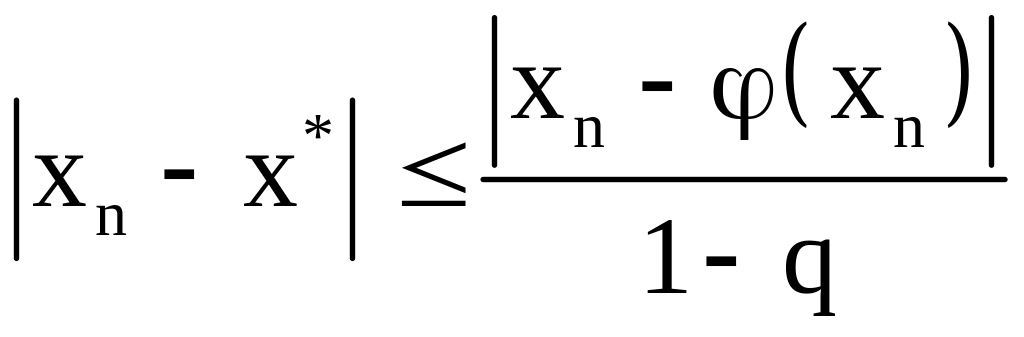или .

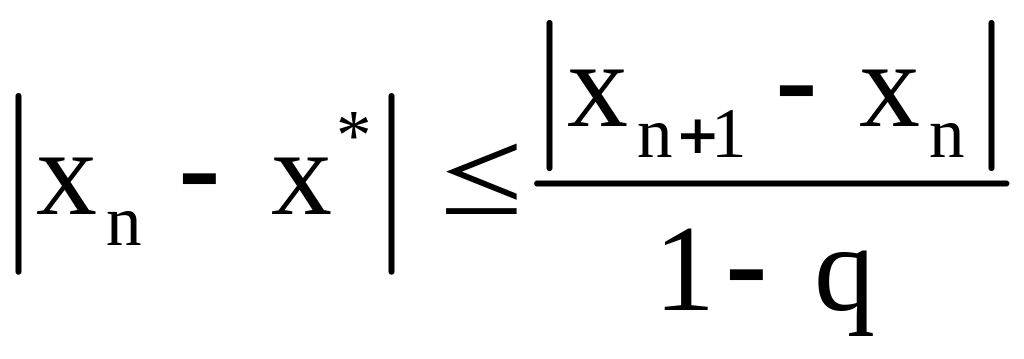Используя предыдущую формулу, можно получить:

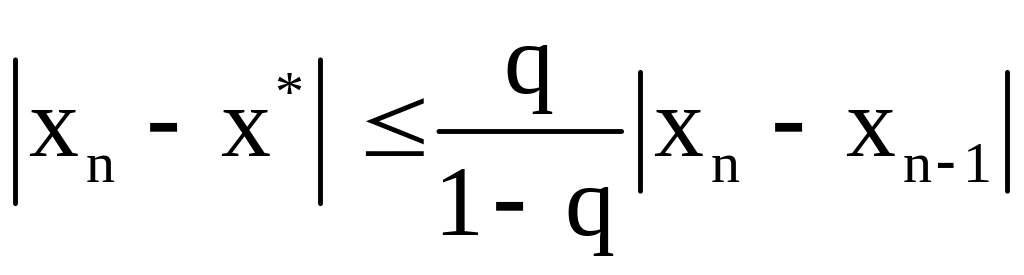. (5)

Перейдём к пределу в равенстве (3), в силу непрерывности функции получим , то есть – корень уравнения (2). Других корней на нет, так как если , то , тогда , где . Равенство нулю будет достигнуто, если . То есть – корень единственный.

Теорема доказана.

Приведение уравнения к виду для обеспечения выполнения неравенства

В общем случае получить подходящую итерационную форму возможно, проведя равносильное преобразование исходного уравнения, например, умножив его на коэффициент : . Прибавив затем к обеим частям уравнения и обозначив можно потребовать выполнения достаточного условия . Отсюда определяется необходимое значение . Так как условие должно выполняться на всем отрезке , то для выбора следует использовать наибольшее значение на этом отрезке, т.е.

. Это соотношение определяет диапазон значений коэффициента , изменяющий величину в пределах .

Обычно принимают .

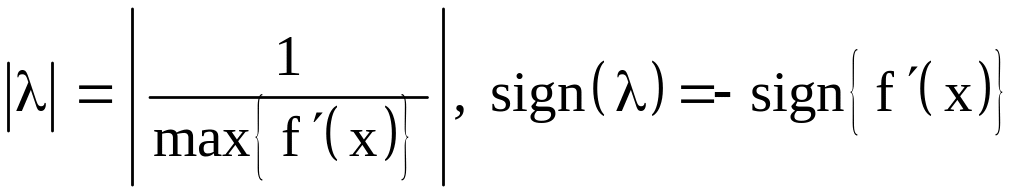На рис. 3–6 показаны четыре случая взаимного расположения линий и и соответствующие итерационные процессы. Рис. 3 и 4 соответствуют случаю , и итерационный процесс сходится. При этом, если (рис. 3), сходимость носит односторонний характер, а если (рис. 4), сходимость носит двусторонний, колебательный характер. Рис. 5 и 6 соответствуют случаю – итерационный процесс расходится. При этом может быть односторонняя (рис. 5) и двусторонняя (рис. 6) расходимость.

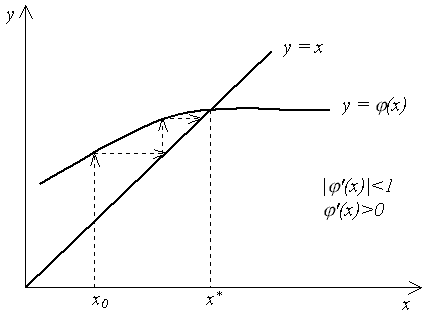
Рис. 3

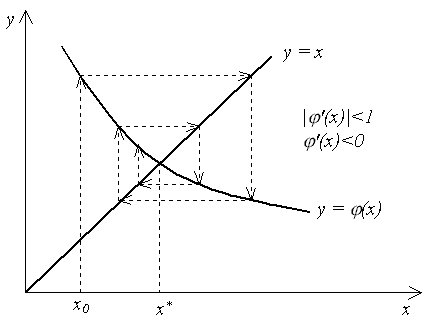
Рис. 4

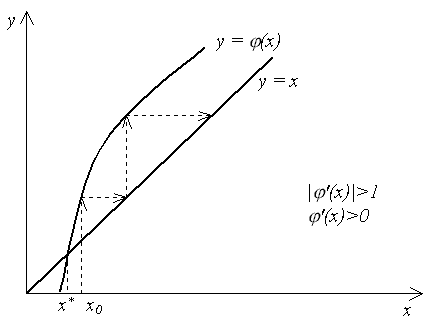
Рис. 5

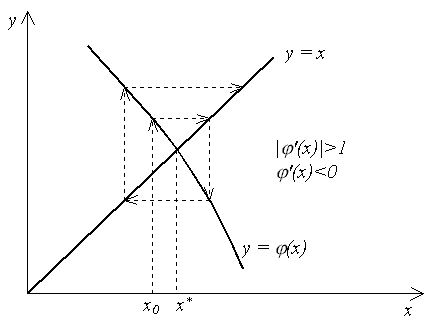
Рис. 6

Погрешность метода. Оценка погрешности была доказана (5).

Критерий окончания. Из оценки (5) следует, что вычисления надо продолжать до выполнения неравенство 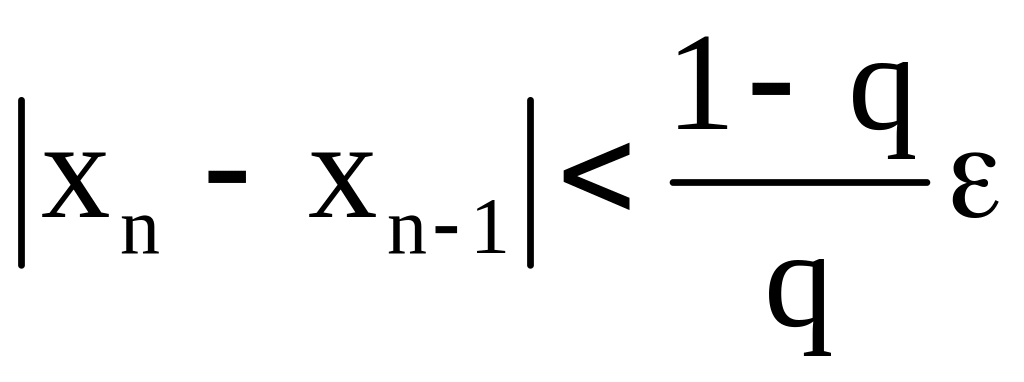. Если же , то оценка упрощается: .

Пример 1. Используем метод простой итерации для решения уравнения с точностью . Преобразуем уравнение к виду:

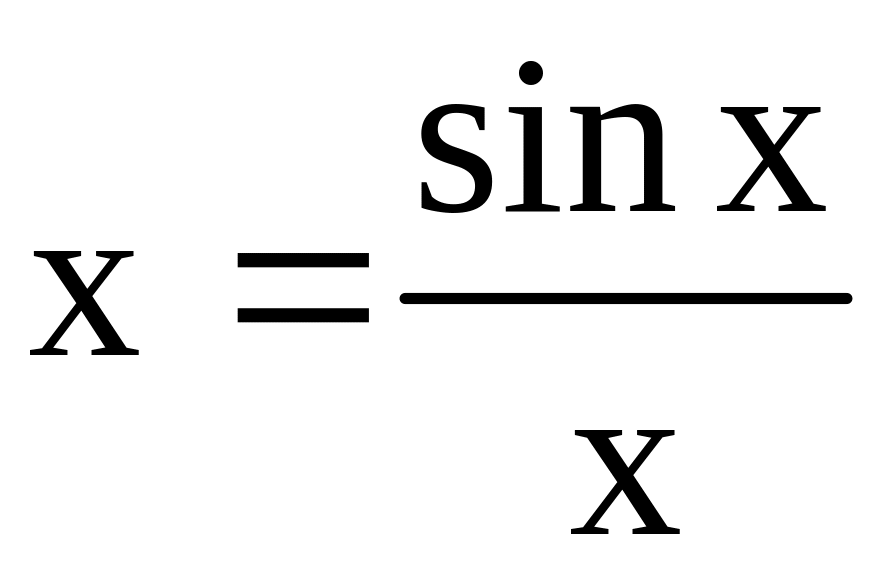, т. е. .

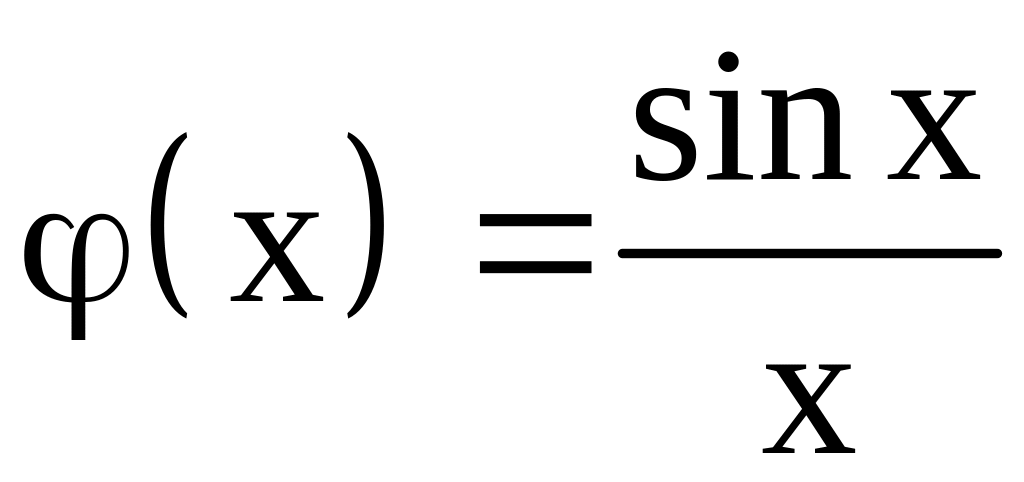Нетрудно убедиться, что корень уравнения находится на отрезке . Вычислив значения на концах отрезка, получим: , а , т. е. функция на концах отрезка имеет разные знаки,

поэтому внутри отрезка есть корень. Расположение корня наглядно иллюстрирует рис. 7.

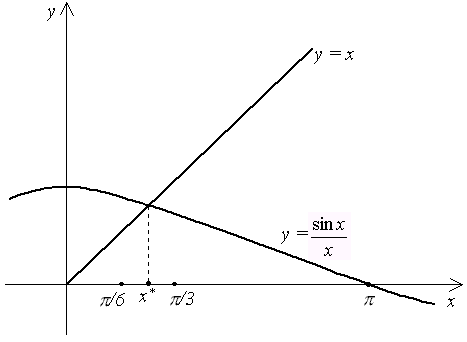
Рис. 7

Подсчитаем первую и вторую производные функции :

.

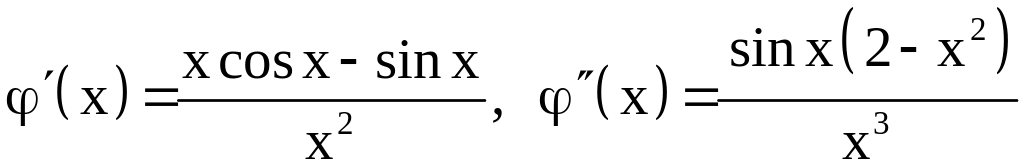Так как на отрезке , то производная монотонно возрастает на этом отрезке и принимает максимальное значение на правом конце отрезка, т. е. в точке . Поэтому справедлива оценка:

.

Таким образом, условие выполнено, и можно воспользоваться критерием окончания вычислений. В табл. 2 приведены приближения, полученные по расчетной формуле. В качестве начального приближения выбрано значение .

Таблица 2

	0	1	2	3	4	5
	1	0,8415	0,8861	0,8712	0,8774	0,8765

Критерий окончания выполняется при , . Сходимость двусторонняя, качественный характер такой сходимости представлен на рис. 4. Приближенное значение корня с требуемой точностью .

Пример 2. Решить методом простой итерации уравнение на отрезке с точностью 0,025. Для решения исходное уравнение приводится к виду . Для выбора величины используем приведенную выше формулу . Тогда расчетная формула имеет вид . В качестве начального приближения можно выбрать верхнюю границу заданного отрезка .

	0	1	2
	1	0,8	0,78

Так как , то .