
- •1. Пассивный транспорт веществ через биологические мембраны. Простая и облегченная диффузия.
- •2. Математическое описание процесса пассивного транспорта
- •3. Активный транспорт ионов. Механизм активного транспорта ионов на примере натрий-калиевого насоса
- •4. Возникновение мембранных потенциалов клетки. Равновесные потенциалы. Уравнение Нернста
- •5. Потенциал покоя клетки
2. Математическое описание процесса пассивного транспорта
Рассмотрим, что заставляет молекулу или ион двигаться через мембрану в нужном направлении без затрат энергии. Для этого представим себе, что мембрана разделяет два водных раствора одинакового состава, но разной концентрации. Если это растворы ионов, то будут разными и электрические потенциалы растворов. Один раствор заполняет клетку и определяет состав цитоплазмы второй – межклеточной жидкости, которая окружает клетку (Рис. 4).
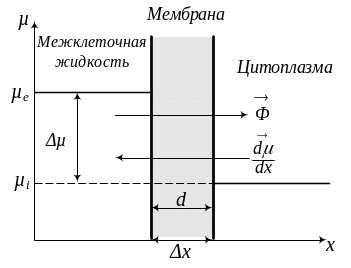
Рис. 4 Схема пассивного переноса вещества через мембрану
В этом случае процесс пассивного переноса вещества через мембрану описывается уравнением Теорелла:
![]() ,
(1)
,
(1)
где Ф – плотность потока диффузии, то
есть количество вещества, которое
переносится за 1 с. через единицу площади
мембраны. Вектор
![]() указывает направление переноса вещества.
Величина С – наибольшая молярная
концентрация вещества, U – подвижность
вещества, которая характеризует скорость
его переноса,
указывает направление переноса вещества.
Величина С – наибольшая молярная
концентрация вещества, U – подвижность
вещества, которая характеризует скорость
его переноса,
![]() – вектор градиента электрохимического
потенциала, который формируется на
мембране.
– вектор градиента электрохимического
потенциала, который формируется на
мембране.
Электрохимический потенциал – это свободная энергия одного моля вещества. Свободная энергия – термодинамический потенциал, который определяет способность какой-либо физико-химической системы совершать полезную работу. Значение равно:
![]() (2)
(2)
Здесь слагаемое 0 определяется энергией химической связи растворенного вещества с растворителем, С – молярная концентрация растворенного вещества, – электрический потенциал раствора, Z – электрический заряд растворенных ионов, который выражен в единицах заряда электрона, F – число Фарадея, R – универсальная газовая постоянная, T – абсолютная температура раствора. Из формулы (2) видно, что каждый из растворов, разделенных мембраной, может иметь свое значение электрохимического потенциала. Обозначим их i и e; где i характеризует цитоплазму (буква i – первая буква слова intra – внутри), e– межклеточную жидкость (e – extra – вне, снаружи) (Рис. 4).
Величина градиента электрохимического
потенциала может быть оценена по формуле:
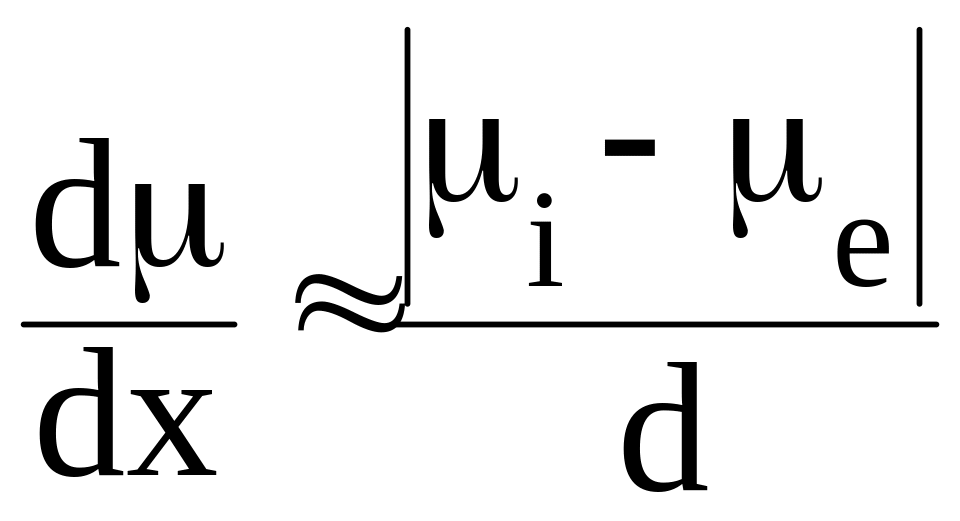 ,
где d – толщина мембраны. Вектор
,
где d – толщина мембраны. Вектор
![]() всегда направлен в сторону больших
значений (рис.4).
всегда направлен в сторону больших
значений (рис.4).
Уравнение Теорелла
показывает, что перенос вещества через
мембрану, есть только тогда, когда
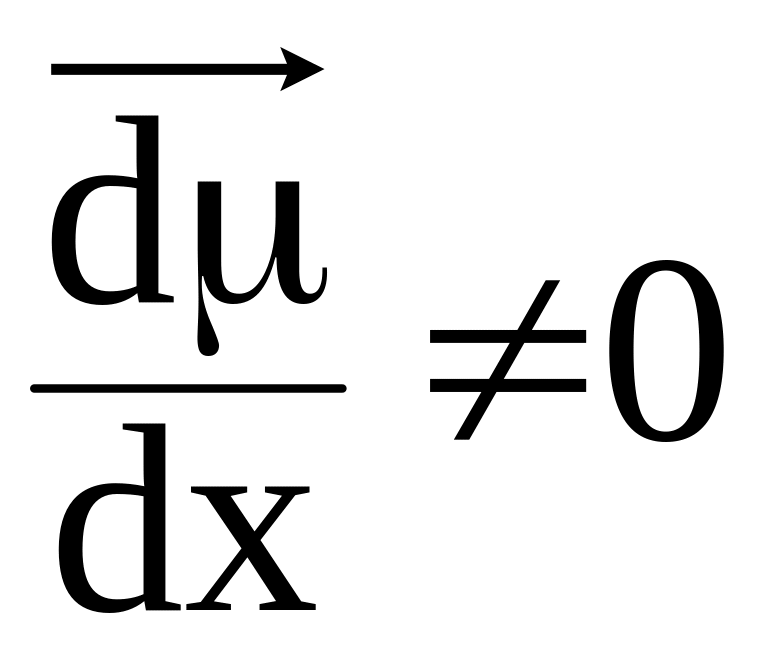 ,
т.е. когда i
e
иначе говоря когда система межклеточная
жидкость-мембрана-цитоплазма
термодинамически неравновесна. Таким
образом, перенос возможен только в
термодинамически неравновесной системе
и градиент электрохимического потенциала
является той силой, которая выполняет
работу по пассивному транспорту вещества.
Знак "–" в формуле (1) указывает на
то, что транспорт происходит всегда в
направлении, которое противоположно
,
то есть в направлении меньших значений
(рис. 4). Перенос
вещества приводит к тому, что i
и e становятся
равны друг другу (i
= e), но тогда,
по уравнению (1), поток диффузии тоже
становится равным нулю: Ф = 0. Пассивный
транспорт прекращается. Наступает
состояние термодинамического равновесия,
в системе межклеточная
жидкость-мембрана-цитоплазма. Это
состояние часто определяется как
состояние покоя для клетки.
,
т.е. когда i
e
иначе говоря когда система межклеточная
жидкость-мембрана-цитоплазма
термодинамически неравновесна. Таким
образом, перенос возможен только в
термодинамически неравновесной системе
и градиент электрохимического потенциала
является той силой, которая выполняет
работу по пассивному транспорту вещества.
Знак "–" в формуле (1) указывает на
то, что транспорт происходит всегда в
направлении, которое противоположно
,
то есть в направлении меньших значений
(рис. 4). Перенос
вещества приводит к тому, что i
и e становятся
равны друг другу (i
= e), но тогда,
по уравнению (1), поток диффузии тоже
становится равным нулю: Ф = 0. Пассивный
транспорт прекращается. Наступает
состояние термодинамического равновесия,
в системе межклеточная
жидкость-мембрана-цитоплазма. Это
состояние часто определяется как
состояние покоя для клетки.
Диффузия ионов через мембрану описывается уравнением Нернста-Планка:
![]() , (3)
, (3)
где
![]() и
и
![]() – векторы градиента концентрации и
электрического потенциала, соответственно.
Таким образом, пассивный перенос ионов
определяется одновременным действием
этих двух величин.
– векторы градиента концентрации и
электрического потенциала, соответственно.
Таким образом, пассивный перенос ионов
определяется одновременным действием
этих двух величин.
При диффузии незаряженных частиц (Z = 0) формула (3) принимает вид:
![]() (4)
(4)
и называется уравнением Фика;
URT = D – коэффициент диффузии.
Тогда (4) можно записать в виде:
![]() или, если учесть, что
или, если учесть, что
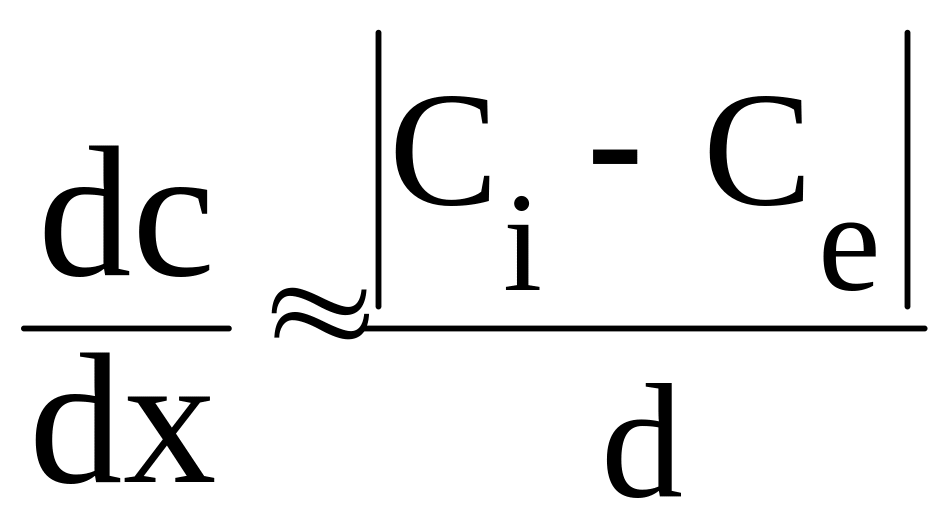 ,
то
,
то
![]() ,
где |Ci
– Ce
| – абсолютное значение разности
концентраций растворенного вещества
в цитоплазме (Сi) и межклеточной
жидкости (Сe).
,
где |Ci
– Ce
| – абсолютное значение разности
концентраций растворенного вещества
в цитоплазме (Сi) и межклеточной
жидкости (Сe).
Если ввести коэффициент проницаемости
мембраны
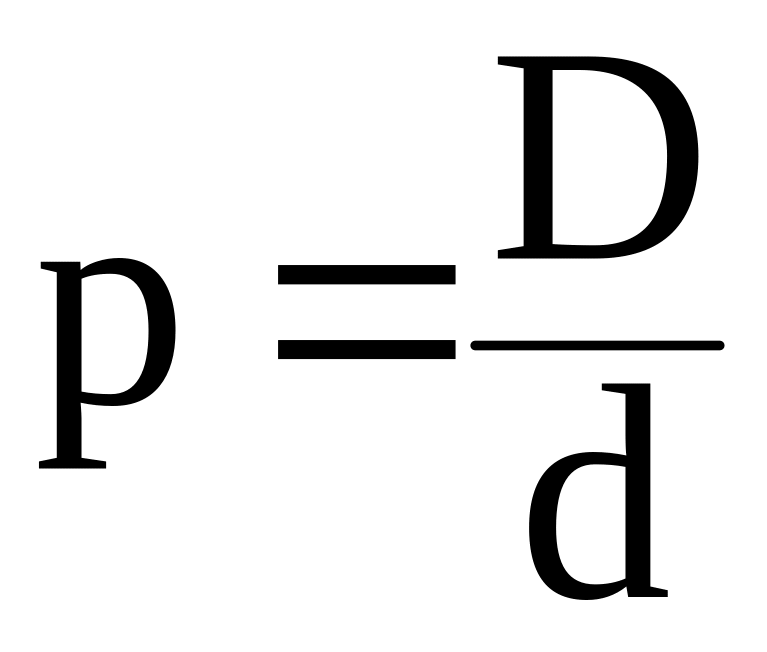 ,
то уравнение Фика примет вид:
,
то уравнение Фика примет вид:
![]() .
.
Таким образом, самое общее уравнение, которое описывает пассивный транспорт вещества через мембрану – это уравнение Теорелла. Из него получают уравнение Нерста-Планка (для ионов) и Фика (для незаряженных частиц).
