
- •Дифракция френеля
- •I. Дифракция френеля
- •При этом нужно помнить, что
- •II. Частные случаи дифракции френеля
- •2.1. Недиафрагмированный волновой фронт
- •2.2. Дифракция на круглом отверстии
- •2.3. Дифракция на круглом непрозрачном экране
- •Описание установки и ее настройка 1
- •Методика измерений
- •Контрольные вопросы
Лабораторная работа № 7
Дифракция френеля
Цель работы: 1. Овладеть методикой демонстрации явления дифракции Френеля на простых объектах с использованием лазера.
2.Овладеть методикой расчета числа зон Френеля в случае дифракции на круглом отверстии.
Оборудование: 1. Прибор ЭСФЭ-1 "Оптика".
2. Линза собирающая (F=163 мм).
3. Метровая линейка с мм делениями - 2 шт.
4. Экран.
5. Набор простых объектов:
а) диафрагма с малым отверстием (d = 1,2 мм), [2-9];
б) маленький круглый экран, [2-8];
в) тонкая нить, [2-7].
ТЕОРИЯ
Способность световых волн огибать препятствия, в результате чего в области геометрической тени наблюдается чередование света и тени, называется дифракцией света. Это явление впервые было обнаружено в 1665 году итальянским ученым Гримальди.
Френель не только объяснил дифракцию света, но и предложил методы ее количественного расчета. Дифракция Френеля наблюдается в сферических волнах или в ограниченных световых пучках.
Высокая степень когерентности и высокая направленность лазерного излучения открывают широкие возможности для изучения дифракционных явлений. Результаты экспериментов с лазерами весьма наглядны и легко воспроизводимы.
В работе исследуется дифракция лазерного излучения на простых объектах: - круглое отверстие [2-9];
- круглый экран [2-8];
- тонкая нить [2-7].
I. Дифракция френеля
При рассмотрении дифракции света Френель исходил из нескольких основных утверждений, принимаемых без доказательства.
Во-первых, следуя принципу Гюйгенса, Френель считал, что для решения задачи о распространении волн, возбуждаемых каким-либо источником S, можно этот источник заменить эквивалентной ему системой фиктивных (виртуальных) вторичных источников S и возбуждаемых ими вторичных волн.
Во-вторых, предположил, что вторичные источники когерентны между собой.
В-третьих, Френель усовершенствовал принцип Гюйгенса, учтя различие фаз элементарных вторичных волн. Измененный принцип носит название принципа Гюйгенса-Френеля. Согласно этому принципу, при распространении в пространстве ограниченных фронтов световых волн свет будет наблюдаться только там, где элементарные волны, испускаемые всеми вторичными источниками, складываясь, (интерферируя), усиливают друг друга; в тех местах, где вторичные волны при сложении гасят друг друга, будет наблюдаться темнота.
На основе принципа Гюйгенса-Френеля можно дать объяснение всем дифракционным явлениям, а также объяснить с точки зрения волновой теории прямолинейное распространение света при безграничном фронте световой волны.
Рассмотрим, как с помощью утверждений Френеля можно рассчитать результирующую амплитуду в некоторой точке.
Возьмем некоторую поверхность S, представляющую собой положение волнового фронта в некоторый момент. Для того, чтобы определить результирующее колебание в точке P, лежащей перед фронтом на расстоянии r0, (рис.1) надо, по Френелю, колебания, которые приходят в эту точку Р от всех элементов поверхности S (вторичных источников), сложить, учитывая их амплитуды и фазы:

Рис. 1
При этом нужно помнить, что
а) фаза определяется длиной пути r , пройденного волнами,
б) амплитуда колебаний, приходящих в точку Р, зависит от размеров площади S , занятой элементарными источниками, расстояния r и угла между нормалью к поверхности S и направлением r.
Для упрощения подсчетов Френель ввел метод зон.
Зона Френеля – участок волнового фронта, выбранный таким образом, что разность хода от двух соседних зон до одной и той же точки экрана отличается на /2.
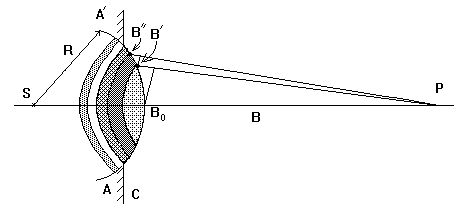
Рис. 2
Пусть свет от точечного источника S проходит через круглое отверстие (диафрагму) в непрозрачном экране (рис. 2). Так как волновой фронт точечного источника по форме представляет собою сферу, то в диафрагме укладывается участок сферического волнового фронта шаровой сегмент AA. Разобьем его на сферические кольца такой ширины, чтобы расстояния от сходственных точек B и B соседних колец до точки P на экране удовлетворяли условию:
![]() .
.
Такой выбор ширины колец приведет к тому, что колебания, приходящие от соседних зон в точку Р, окажутся в противофазе. Вычислим результирующую амплитуду колебаний в точке Р. Для этого определим величину площади одной из зон Френеля (рис. 3). Эту величину S найдем как разность площадей к и (к - 1) сферических колец:
S = Sк Sк-1. (1)
где
![]()
![]() ,
,
![]() .
.

Рис. 3
Поверхность шарового сегмента выразим как сумму площадей всех к зон Френеля, начиная с первой:
Sк = 2 Rh , (2)
Найдем выражение для h, где h – высота шарового сегмента, направленности которого укладывается к зон Френеля.
Из рис.3 видно, что
![]() ,
,
![]() ,
,
откуда считая h20,
![]() ,
,
но ![]() , тогда
, тогда
![]() ;
;
при
![]() , тогда
, тогда
![]() ,
,
откуда
![]() .
(3)
.
(3)
Подставляя
(3) в (2), получим
![]() .
.
Используя выражение (1), выразим площадь одной зоны Френеля:
![]() .
(4)
.
(4)
Как видно, площадь каждой зоны не зависит от номера зоны, следовательно, площади всех зон приблизительно равны. Это можно было предположить без вывода, так как количество вторичных источников, размещенных в каждой зоне Френеля и посылающих свет в точку Р, должно быть одинаково, иначе результат сложения волн в точке Р не будет предсказуем. Таким образом, от величины S результирующая амплитуда не зависит. Амплитуда будет зависеть от расстояния r, пройденного волной от каждой зоны, причем, чем больше номер зоны, тем больше r. Кроме того, с ростом номера зоны растет и угол . Освещенность экрана определяется углом падения света на экран:
![]() .
.
Угол (рис.1) угол падения света на экран.
Исходя из вышесказанного, можно утверждать, что амплитуда колебаний с увеличением номера зоны будет монотонно убывать
![]()
При сложении колебаний от двух соседних зон нужно учитывать, что в точку Р эти колебания приходят в противофазе, поэтому
![]() ,
,
где знак (+) для к – нечетного номера зоны,
знак (-) для к – четного.
Разобьем амплитуды нечетных зон на два слагаемых
![]() ,
,
тогда при к – нечетном имеем:
![]() ;
;
при к – четном имеем:
![]() .
.
Учитывая, что к-1 к к+1 , введем подстановку:
![]() ,
,
тогда
![]() ,
(5)
,
(5)
где () при к – четном,
(+) при к – нечетном.
