Порядок работы
Формулы:
или
,
, 
, 
,
, 
В колебаниях годового стока, как и в колебаниях годовых осадков, прослеживается цикличность – последовательная смена многоводной и маловодной фаз, причина которых – циклическое изменение климата.
Водный цикл – сочетание многоводных и маловодных фаз, а так же лет средней водности. Длительность циклов не одинакова. Если в период наблюдения входит целый цикл и, к примеру, еще многоводная фаза, то среднее значение будет завышено, поэтому в период для определения нормы стока включают законченные водные циклы, отдельные фазы исключают. Репрезентативный результат наблюдений оценивают по интегральной кривой стока, которая представляет собой график (по оси абсцисс – год наблюдения, по оси ординат - соответствующее Ki-1).
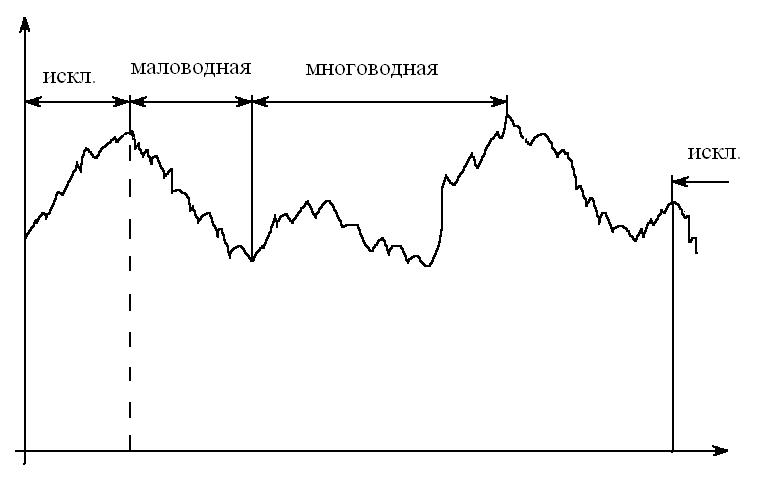
Рис. 6 Интегральная кривая стока
Анализируя интегральную кривую стока можно выделить один полный цикл водности, включающий маловодную и многоводную фазы. Для расчета гидрологических характеристик, необходимо использовать не менее двух полных циклов водности (для репрезентативного ряда). Значения коэффициента вариации можно определить либо методом моментов, либо методом наибольшего правдоподобия.
Сущность метода моментов: параметры кривой распределения выражаются через значения моментов эмпирического распределения с поправками на ликвидационное смещение. При этом большое влияние оказывают крайние члены ряда.
Сущность метода наибольшего
правдоподобия: наиболее вероятным
считать такое значение параметра, при
котором функция правдоподобности
достигает наибольшего значения. Этот
метод позволяет определить значения
коэффициента вариации при помощи
статистик
,
которые в свою очередь рассчитывают по
формулам:
и
Аналитическая и эмпирическая кривые обеспеченности
Эмпирическая кривая обеспеченности – график зависимости расходов от обеспеченности.
Рис. 7 Эмпирическая кривая обеспеченности
Полученная на основе ограниченного числа данных наблюдения – эмпирическая кривая обеспеченности практически не освещает концевых участков, относящихся к области малых и больших значений характеристик стока. Однако, именно эти участки кривой обеспеченности представляют наибольший интерес для решения инженерно-гидрологических задач. На основании имеющейся статистической выборки ставиться задача построения кривой обеспеченности, которая наиболее полно отражала бы характер колебания гидрологических величин. Эта задача решается путем применения аналитических функций распределения. В гидрологической практике применяют интегральную форму аналитической функции распределения, которую часто называют функцией распределения ежегодных вероятностей превышения, а график функции – аналитической кривой обеспеченности.
Расчетно-гидрологические характеристики определяются с помощью двух типов кривых:
- трехпараметрического гамма-распределения
- биноминального распределения.
Для построения аналитической и эмпирической кривых обеспеченности, используются клетчатка вероятности (клетчатка Хазена).
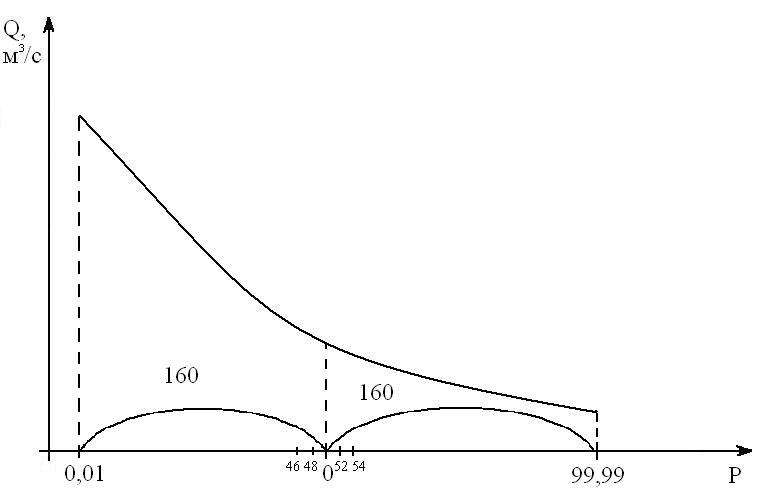
Рис. 8 Клетчатка Хазена