2.6. Сравнение дисперсий двух нормальных распределений

Пусть случайные величины X и Y распределены по нормальному закону. По выборкам значений X объема n и Y объема m требуется проверить нулевую гипотезу H₀ о равенстве дисперсий этих случайных величин: ²(X) = ²(Y).

Как обычно предположим вначале, что математические ожидания X и Y известны и рассмотрим случайную величину

, s_x > s_y. (2.7)

Указанная случайная величина распределена по закону Фишера-Снедекора со степенями свободы (n1) и (m1).

Пример 2.5. По двум независимым выборкам значений нормально распределенных случайных величин X и Y, объемы которых равны 9 и 6, найдены выборочные дисперсии = 23,27 и = 8,91. При уровне значимости = 0,1 проверить двустороннюю нулевую гипотезу H₀: D(X) = D(Y) .

Решение. Поскольку s_X > s_Y ,то находим значение критерия Фишера-Снедекора: . Число степеней свободы 8 и 5, а значение , по таблице критических значений распределения Фишера-Снедекора находим F_кр = 4,82. Поскольку F_набл < F_кр, нулевая гипотеза принимается.

2.7. Критерии согласия

Критерии согласия предназначены для проверки того, что нулевая гипотеза H₀ о виде распределения соответствует выборочным данным.

Рассмотрим таблицу выборочного закона распределения некоторого вариационного ряда. Наша задача состоит в том, чтобы, во-первых, подобрать соответствующий закон теоретического распределения. Предположим, что нам удалось найти некоторую теоретическую функцию плотности f(x), приближённо соответствующую данному вариационному ряду. Тогда, во-вторых, надо проверить насколько точно наши статистические данные соответствуют выбранному теоретическому распределению. В этом случае альтернативная гипотеза не выдвигается. Схема проверки нулевой гипотезы практически не изменяется.

Представим функцию f(x) виде гистограммы (см. рис.2.2), разбив размах выборки и предполагаемой генеральной совокупности на r разрядов.

Р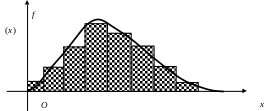 ис. 2.2

Представим теоретические и полученные после предварительной обработки выборки частоты попадания случайной величины в соответствуюший разряд в виде следуюшей таблицы:

Интервалы	x1; x2	x2; x3	…	xr; xr+1
Теоретические частоты	n1	n2		nr
Эмпирические частоты	m1	m2	…	mr

Предполагается, что объем выборки равен n, т.е.

m₁ + m₂ +…+ m_r = n. (2.8)

По теоретическому закону распределения, заданному с помощью функции f(x), находим вероятности попадания случайной величины X в каждый из данных разрядов: p₁, p₂, …, p_k. Затем вычисляем теоретические частоты n_i, умножив вероятности на объем выборки: n_i = np_i. В качестве критерия согласия применяют критерий ("хи-квадрат") Пирсона:

. ( 2.9)

Распределение зависит только от одного параметра k  числа степеней свободы. Число степеней свободы k равно числу разрядов r минус число независимых условий, наложенных на частоты m_i.

Условие (2.8) накладывается всегда. Часто используют еще два условия: равенство среднего значения и математического ожидания и равенство выборочной и теоретической дисперсий. Поэтому обычно выполняется равенство

k = r  3. (2.10)

Пример 2.6. При уровне значимости = 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты

mi	4	27	73	135	128	78	50	5
ni	5	27	70	125	137	82	48	6

Решение. Вычислим значение критерия Пирсона

= = 2,457.

Число степеней свободы в данном случае k = 8  3 = 5. По таблице критических точек распределения по уровню значимости = 0,05 и числу степеней свободы k = 5 находим = 11,1. Итак, < , поэтому можно принять нулевую гипотезу о нормальном распределении генеральной совокупности.

Замечание. Критерий Пирсона, как показывает практика, успешно применяется для выборок объема n>50 и если все частоты n_i = np_i>5.