- •1.Теоретичні відомості.
- •1.1.Чисельні методи. Застосування. Основні принципи побудови.
- •1.2. Чисельне розв’язання трансцендентних рівнянь. Опис методів дихотомії (половинного ділення), хорд, дотичних, комбінованого методу хорд та дотичних
- •Алгоритм методу
- •Метод хорд.
- •1.3. Чисельне інтегрування. Методи лівих, правих та середніх прямокутників. Методи трапецій та парабол.
- •1.4. Використання системи Math Cad для розв’язання технічних завдань. Основні особливості та методи роботи із системою.
- •Математичні вирази.
- •Типи даних.
- •1.5. Використання табличного процесору Excel для розв’язання технічних завдань. Основні особливості та методи роботи із системою.
- •1.6. Використання алгоритмічної мови Pascal для розв’язання технічних завдань. Основні особливості та методи роботи із оболонкою Turbo-Pascal
- •Типи даних в Паскалі
- •2. Постановка задачі, із індивідуальним завданням.
- •Завдання на практичну частину із використанням системи Math Cad.
- •2.2. Завдання на розрахункову частину із використанням системи Excel.
- •2.2. Завдання на розрахункову частину із використанням системи Excel.
- •Завдання на алгоритмічну частину із використанням мови Pascal.
- •6.Порівняння ефективності чисельних методів, згідно індивідуального завдання.
- •7.Оцінка збіжності результатів розрахунків за допомогою табличного процесору Excel із результатами, які були отримані за допомогою систем Math Cad та програм згідно індивідуального завдання.
- •8.Висновки.
1.3. Чисельне інтегрування. Методи лівих, правих та середніх прямокутників. Методи трапецій та парабол.
Метод прямокутників.
Найпростішим
методом наближеного обчислення інтеграла
є метод прямокутників, геометрична
інтерпретація якого зводиться до
знаходження визначеного інтеграла як
суми площ N
прямокутників (з висотою f(x)
та основою h=
![]() xi=xi+1-xi),
отриманих розділень відрізка[a,b]
на N
рівних частин, до того ж якщо розділити
на прямокутники зліва на право, то
отримаємо формулу лівих прямокутників:
In=
xi=xi+1-xi),
отриманих розділень відрізка[a,b]
на N
рівних частин, до того ж якщо розділити
на прямокутники зліва на право, то
отримаємо формулу лівих прямокутників:
In=![]() f(x)dx»
f(x)dx»![]() Si=h[f(x0)+f(x1)+...+f(xn-1)]=
Si=h[f(x0)+f(x1)+...+f(xn-1)]=![]()
![]() f(xi);
якщо
ж розділити на N
прямокутників справа на ліво, то отримаємо
формулу правих прямокутників:
f(xi);
якщо
ж розділити на N
прямокутників справа на ліво, то отримаємо
формулу правих прямокутників:
Iпр=
f(x)dx»h[f(xn)+...+f(x1)]=![]()
![]() f(xi).
f(xi).
Метод трапецій.
Суть
методу трапеції, полягає в тому, що
інтеграл обчислюється по-іншому, відрізок
інтегрування поділяється на N
рівних відрізків, всередині яких
підінтегральна крива f(x)
замінюється кусково- лінійною функцією
j(x),
отриманою стягуванням ординат N
відрізків хордами.
Обчислення
визначеного інтеграла зводиться до
знаходження сум площ Si
прямокутних трапецій N.
Площа кожної
такої трапеції визначається як:
Si=h
![]() (f(xi)+f(xi+1)).
(f(xi)+f(xi+1)).
Отже,формулатрапеції:
I=
![]() »
Si=h(
»
Si=h(
![]() f(x0)+f(x1)+f(x2)+...+f(xn-1)+
f(xN)=
=
f(x0)+f(x1)+f(x2)+...+f(xn-1)+
f(xN)=
=
![]() [
(f(x0)+f(xn))+
[
(f(x0)+f(xn))+
![]() f(xi)].
f(xi)].
![]() Графічна
модель
Похибка обчислення інтеграла
за формулою трапецій оцінюється як
Графічна
модель
Похибка обчислення інтеграла
за формулою трапецій оцінюється як
![]() Де М2
–максимальне
значення другої похідної.f(x)
при
Де М2
–максимальне
значення другої похідної.f(x)
при
![]() h-крок
обчислень.
h-крок
обчислень.
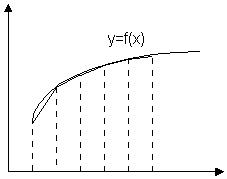
Рис.1.3.1.
Метод парабол.
Цей метод також використано у курсовій роботі, близький до методу трапецій у тій частині, що інтегрування проводиться шляхом поділу відрізка інтегрування [а, b] на множину відрізків (N пар відрізків). Однак, з метою збільшення точності наближеного інтегрування на кожному відрізку [Xi, Xi+2] підінтегральної функції f(x) замінюють квадратичною параболою j(x), обчислення визначеного інтеграла зводиться до обчислення суми N криволінійних трапецій Si: I= f(x)dx» Si [1].
|
|
|
|
Рисунок 1.3.2.
Графічна модель.
Площа
кожної такої трапеції визначається за
формулою Сімпсона:
Si=
![]() [f(xi)+4f(
[f(xi)+4f(
![]() xi+1)+f(xi+2)],
тобто
xi+1)+f(xi+2)],
тобто
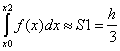 (y0+4y1+y2),
(y0+4y1+y2),
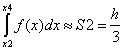 (y2+4y3+y4),
(y2+4y3+y4),
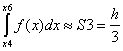 (y4+4y5+y6),
. . . . . . . . . . . . . . . . . . . . . . .
(y4+4y5+y6),
. . . . . . . . . . . . . . . . . . . . . . .
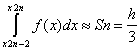 (y2n-2+4y2n-1+y2n),
Тоді
чисельне значення визначеного інтеграла
на відрізку [a,b] дорівнюватиме сумі
інтегралів, тобто
(y2n-2+4y2n-1+y2n),
Тоді
чисельне значення визначеного інтеграла
на відрізку [a,b] дорівнюватиме сумі
інтегралів, тобто
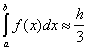 [y0+y2n+4(y1+...+y2n-1)+2(y2+...+y2n-2)],
або
[y0+y2n+4
y2i-1+2
y2i],(1.8)
де h =(b-a)/2N.
Похибка
обчислення інтеграла за формулою
Сімпсона оцінюється як
[y0+y2n+4(y1+...+y2n-1)+2(y2+...+y2n-2)],
або
[y0+y2n+4
y2i-1+2
y2i],(1.8)
де h =(b-a)/2N.
Похибка
обчислення інтеграла за формулою
Сімпсона оцінюється як
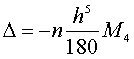 де
М4
–максимальне
значення четвертої похідної.
f(x)
при
,
h-крок
обчислень.
де
М4
–максимальне
значення четвертої похідної.
f(x)
при
,
h-крок
обчислень.
1.4. Використання системи Math Cad для розв’язання технічних завдань. Основні особливості та методи роботи із системою.
MathCAD працює з документами. З погляду користувача, документ - це чистий аркуш паперу, на якому можна розміщати блоки трьох основних типів: математичні вирази, текстові фрагменти і графічні області.
Розташування нетекстових блоків у документі має принципове значення – зліва направо і зверху вниз.