Сложение векторов

Скаляры можно складывать, умножать и делить так же, как обычные числа.

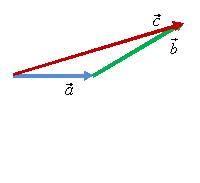
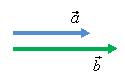
Поскольку вектор характеризуется не только числовым значение, но и направлением, сложение векторов не подчиняется правилам сложения чисел. Например, пусть длины векторов a = 3 м, b = 4 м, тогда a + b = 3 м + 4 м = 7 м. Но длина вектора не будет равна 7 м (рис. 1).

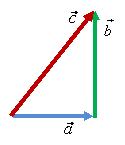
Рис. 1.

Для того, чтобы построить вектор (рис. 2), применяются специальные правила сложения векторов.

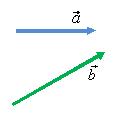
Рис. 2.

А длину вектора суммы определяют по теореме косинусов , где – угол между векторами и .

Правило треугольника

В зарубежной литературе этот метод называют «хвост к голове».

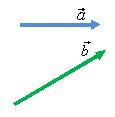
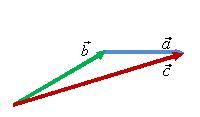
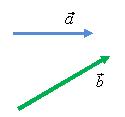
Для того чтобы сложить два вектора и (рис. 3, а) нужно переместить вектор параллельно самому себе так, чтобы его начало совпадало с концом вектора (рис. 3, б). Тогда их суммой будет вектор , начало которого совпадает с началом вектора , а конец — с концом вектора (рис. 3, в).

     

а                                         б                                                    в      

Рис. 3.

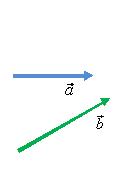
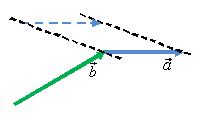
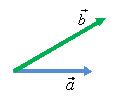
Результат не поменяется, если перемещать вместо вектора вектор (рис. 4), т.е. (свойство коммутативности векторов).

     

а                                         б                                                    в      

Рис. 4.

"Правило треугольников" Пример 1

Увеличить Flash

"Правило треугольников" Пример 2

Увеличить Flash

Рис. 5.

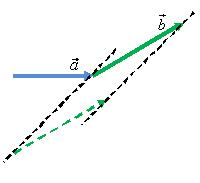
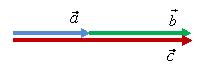
При помощи правила треугольника можно сложить два параллельных вектора и (рис. 6, а) и и (рис. 7, а). Суммы этих векторов и изображены на рис. 6, б и 7, б. Причем, модули векторов и .

  

а                                         б

Рис. 6.

  

а                                         б

Рис. 7.

Правило треугольника можно применять при сложении трех и более векторов. Например, (рис. 8).

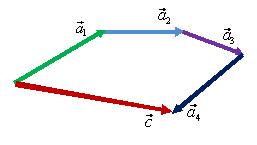
Рис. 8.

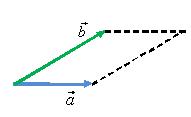
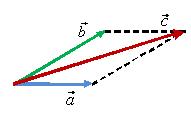
Правило параллелограмма

Для того чтобы сложить два вектора и (рис. 9, а) нужно переместить их параллельно самим себе так, чтобы начала векторов и находились в одной точке (рис. 9, б). Затем построить параллелограмм, сторонами которого будут эти вектора (рис. 9, в). Тогда суммой будет вектор , начало которого совпадает с общим началом векторов, а конец — с противоположной вершиной параллелограмма (рис. 9, г).

  

а                                         б

  

в                                         г

Рис. 9.

"Правило параллепипеда"

Увеличить Flash

Рис. 10.

Вычитание векторов

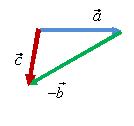
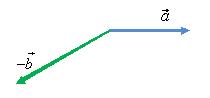
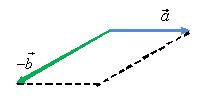
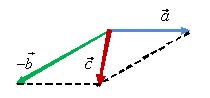
Для того чтобы найти разность двух векторов и (рис. 11) нужно найти вектор (см. Умножение вектора на скаляр) по правилу треугольника (рис. 12) или по правилу параллелограмма (рис. 13).

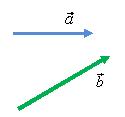
Рис. 11

      

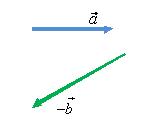
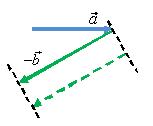
а                                       б                                       в

Рис. 12.

  

а                                            б    

  

б                                            в    

Рис. 13.

Вектор. Определение. Упорядоченную совокупность ( x₁, x₂, ... , x _n ) n вещественных чисел называют n-мерным вектором, а числа x_i ( i = ) - компонентами, или координатами, вектора.

Вектор. Смешанное произведение. Если векторное произведение двух векторов а и b скалярно умножается на третий вектор c, то такое произведение трех векторов называется смешанным произведением и обозначается символом a b c.