Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Транспонированная матрица

С каждой матрицей A = (a_ij) размера связана матрица B = (b_ij) размера вида

Такая матрица называется транспонированной матрицей для A и обозначается так A^T. Транспонированную матрицу можно получить, поменяв строки и столбцы матрицы местами. Матрица A = (a_ij) размера при этом преобразовании станет матрицей размерностью .

Умножение матрицы на число

Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен

Свойства умножения матриц на число

1. 1*A = A;

2. (Λβ)A = Λ(βA)

3. (Λ+β)A = ΛA + βA

4. Λ(A+B) = ΛA + ΛB

Сложение матриц

Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен

Свойства сложения матриц

5.коммутативность;

6.ассоциативность;

7.сложение с нулевой матрицей;

8.существование противоположной матрицы;

Все свойства линейных операций повторяют аксиомы линейного пространства и поэтому справедлива теорема:

Множество всех матриц одинаковых размеров MxN образуют линейное пространство над полем P(полем всех действительных или комплексных чисел), поэтому каждая матрица является и вектором этого пространства.

Умножение матриц

Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

Количество столбцов в матрице A должно совпадать с количеством строк в матрице B. Если матрица A имеет размерность , B — , то размерность их произведения AB = C есть .

Свойства умножения матриц

1.Ассоциативность;

2.произведение не коммутативно;

3.произведение коммутативно в случае умножения с единичной матрицей;

4.справедливость дистрибутивного закона;

5.(ΛA)B = Λ(AB) = A(ΛB);

Ранг матрицы

Количество линейно независимых строк матрицы называют строчным рангом матрицы, а количество линейно независимых столбцов матрицы называют столбцовым рангом матрицы. В действительности, оба ранга совпадают. Их общее значение и называется рангом матрицы.

Другой эквивалентный данному подход заключается в определении ранга матрицы, как максимального порядка отличного от нуля минора матрицы.

ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ, ДЕТЕРМИНАНТ [determinant] — число, соответствующее квадратной матрице и полученное путем ее преобразования по определенному правилу. Обычное обозначение (для матрицы A): det A. Напр., определитель (второго порядка) матрицы

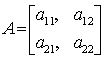
обозначается

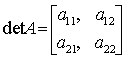
и вычисляется следующим образом:

det A = a₁₁a₂₂ — a₁₂a₂₁.

В общем случае (для квадратной матрицы порядка n) из элементов матрицы A сначала составляют все возможные произведения из n сомножителей каждое, содержащие по одному элементу из каждой строки и по одному элементу из каждого столбца, затем эти произведения складываются по определенному правилу.

Определитель матрицы, в которой вычеркнуты произвольная строка (напр. i-я), и произвольный столбец (напр. j-й), называется минором. Он имеет (n – 1)-й порядок, т. е. порядок на 1 меньше, нежели исходный определитель.