4. Принятие решения в условиях риска

Принятие решения в условиях риска характеризуется тем, что поведение среды имеет случайный характер, причем в этой случайности имеются закономерности стохастического типа.

Как известно из теории вероятностей, наиболее естественной числовой характеристикой случайной величины является ее математическое ожидание. Таким образом, в игре с природой ориентация на математическое ожидание выигрыша есть фактически ориентация на средний выигрыш, при многократном повторении этой игры. Однако при единичном испытании этот критерий должен быть трансформирован с учетом возможных отклонений случайной величины от ее среднего значения.

В теории вероятностей в качестве меры отклонения случайной величины от ее среднего значения обычно берется дисперсия или среднеквадратическое отклонение. При этом среднеквадратическое отклонение рассматривают как показатель риска. Тем самым получаем задачу двухкритериальной оптимизации, где в качестве критериев выступают М и .

Предпочтение альтернатив будем устанавливать по обобщенному критерию вида

q(М, ) = М – .

Пусть ) – некоторое множество альтернатив, каждая из которых характеризуется парой показателей ( ). Зафиксируем какие-то две альтернативы = ( ) и = ( ). Находим: q( )= - ,

q( )= - .

Возможны два случая:

а) Альтернативы сравнимы по Парето. Пусть, например,

_Par

. Тогда и , значит, - - , т.е. q( ) q( ). Таким образом, независимо от меры несклонности принимающего решение к риску, альтернатива более предпочтительна, чем альтернатива .

б) Альтернативы несравнимы по Парето. Пусть, например, , тогда (т.е. больший ожидаемый выигрыш здесь всегда сопровождается большим риском). Условие - - равносильно тому, что λ .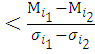

Таким образом, в этом случае

, если λ ,

, если λ .

Положим = min { } – нижняя граница несклонности к риску, = max { } – верхняя граница несклонности к риску.

На основании б) для человека не склонного к риску, получаем правило.

ПРАВИЛА: а) Если у принимающего решение его субъективный показатель несклонности к риску меньше нижней границы, то для него ранжирование множества Парето-оптимальных альтернатив по обобщенному критерию совпадает с ранжированием по показателю ожидаемого выигрыша (т.е. более предпочтительной будет альтернатива, для которой больше ожидаемый выигрыш).

б) Если у принимающего решение его субъективный показатель несклонности к риску больше верхней границы, то для него ранжирование множества Парето-оптимальных альтернатив по обобщенному критерию совпадает с ранжированием по показателю риска ( более предпочтительной будет та альтернатива, для которой меньше риск).

Пример. Фирма может выпускать продукцию одного из следующих шести видов: зонты(З), куртки(К), плащи(П), сумки(С), туфли (Т), шляпы(Ш). Глава фирмы должен принять решение, какой из этих видов продукции выпускать в течение предстоящего летнего сезона. Прибыль фирмы зависит от того, каким будет лето – дождливым, жарким или умеренным, и определяется по таблице. Выбор какого варианта производства будет оптимальным?

	Д	Ж	У
З	80	60	40
К	70	40	80
П	70	50	60
С	50	50	70
Т	75	50	50
Ш	35	75	60

Предположим, что вероятность дождливого, жаркого и умеренного лета равна соответственно 0,2; 0,5; 0,3. Найдем ожидаемые выигрыши, соответствующие имеющимся альтернативам:

М_з= 80

М_к= 70

М_п= 70

М_с= 50

М_т= 75

М_ш= 35

Тогда используя формулу дисперсии получим:

D_з=196; D_к=336; D_п=61; D_с=84; D_т=100; D_ш=231,5.

Среднеквадратические отклонения рассматриваемых случайных величин таковы:

= 14; 18,3; 7,8; 9,2; = 10; = 15,2 .

Представим рассматриваемые альтернативы точками на координатной плоскости переменных (М, ), получим рисунок, из которого находим Парето-оптимальное множество {З,П,Ш}.

M

.

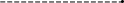
0

Оптимальное решение можно найти с помощью обобщенного критерия

q(М, ) = М – .

Получим: q(З) = 58-14λ, q(С) = 56-9,2λ, q(К) = 58-18,3 λ,

q(Т) = 55-10λ, q(П) = 57-7,8λ, q(Ш) = 62,5-15,2λ.

Найдем нижнюю и верхнюю границы меры несклонности к риску.

Имеем:

= = 0,16; = 3,8;

= = 0,74.

Отсюда

= min (0.16; 3,8; 0,74) = 0,16, = mаx (0.16; 3,8; 0,74) = 3,8.

Таким образом, интервал (0, ) разбивается на три интервала: (0;0,16) – зона малой несклонности к риску (зона малой осторожности); (3,8; + ) – зона большой несклонности к риску (зона большой осторожности); [0,16; 3,8] – зона неопределенности.

Согласно правилу получаем:

1. Если для принимающего решение его мера несклонности к риску 0 λ 0,16, то для него ранжирование множества Парето-оптимальных альтернатив совпадает с их ранжированием по величине ожидаемого выигрыша: Ш З≻П; при этом оптимальной будет альтернатива Ш;

2. Если для принимающего решение его мера несклонности к риску λ>3,8, то для него ранжирование множества Парето-оптимальных альтернатив совпадает с их ранжированием по показателю риска:

П З≻Ш; при этом оптимальной будет альтернатива П.

Рассмотрим теперь случай, когда мера несклонности принимающего решение к риску попадает в зону неопределенности. Возьмем, например, λ=2. Тогда : q(З) = 58–14 , q(П) = 57–7,8 , q(Ш) = 62,5–15,2 = 32,1. Таким образом, в этом случае предпочтение для пары (З,Ш) определяется по величине ожидаемого выигрыша, а для пары (П, Ш ) – по величине риска.

Ответ: При λ > 3,8 оптимальной будет альтернатива П; при 0 λ 0,16 – альтернатива Ш; в зоне неопределенности (например, λ=2) для пары (З,Ш) – альтернатива Ш, для пары (П,Ш) – альтернатива П.