
- •Передмова
- •§1. Основні поняття
- •§2. Позиційні задачі на побудову
- •§3. Перспектива точки
- •§4 Перспектива прямих часткового та особливого розміщення
- •§ 5 Перспектива прямої загального розміщення
- •§6. Взаємне розташування прямих
- •§7 Зображення площини в перспективі
- •§8 Перспективний масштаб
- •§8 Масштабна шкала та її практичне застосування
- •§9 Способи розв’язання метричних задач на картині
§7 Зображення площини в перспективі
В
 геометрії площину задають різними
способами: трьома точками що не лежать
на одній прямій (Рис. 39),
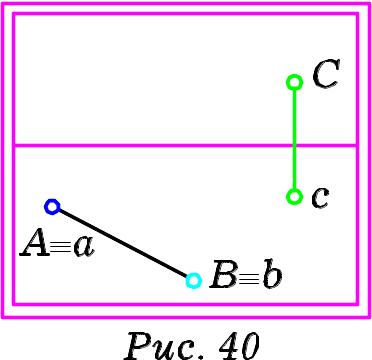
прямою і точкою, що не лежить на цій
прямій (Рис. 40), двома
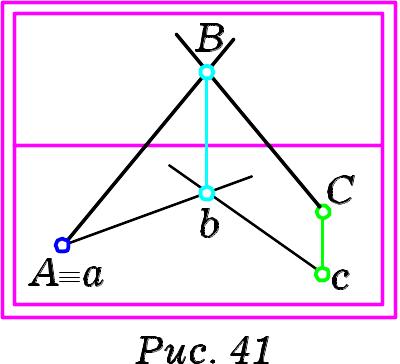
прямими, що перетинаються (Рис. 41),
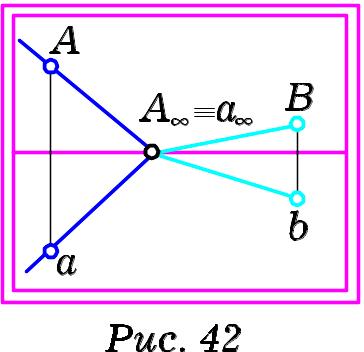
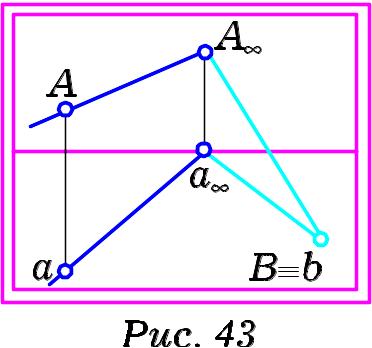
двома паралельними прямими (Рис. 42-43).
Жоден із вказаних способів задання
площини на картині не дає достатньої
наочності. Площина, зображена на
картині многокутником, зокрема
трикутником (Рис.44),
більш наочна. Для досягнення максимальної
наочності та зручності, площину в
перспективі задають слідами.
геометрії площину задають різними
способами: трьома точками що не лежать
на одній прямій (Рис. 39),
прямою і точкою, що не лежить на цій
прямій (Рис. 40), двома
прямими, що перетинаються (Рис. 41),
двома паралельними прямими (Рис. 42-43).
Жоден із вказаних способів задання
площини на картині не дає достатньої
наочності. Площина, зображена на
картині многокутником, зокрема
трикутником (Рис.44),
більш наочна. Для досягнення максимальної
наочності та зручності, площину в
перспективі задають слідами.
П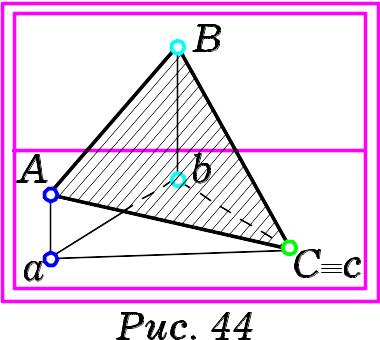
 ід
слідами площини в перспективі
розуміють лінії її перетину з предметною
та картинною площинами. Лінію перетину
з предметною площиною називають
предметним слідом, лінію перетину
з картинною площиною - картинним
слідом площини.
ід
слідами площини в перспективі
розуміють лінії її перетину з предметною
та картинною площинами. Лінію перетину
з предметною площиною називають
предметним слідом, лінію перетину
з картинною площиною - картинним
слідом площини.
Н
 а
рис. 45, а задано площину
а
рис. 45, а задано площину
![]() ,
яка перетинає основу картини в
точці
,
яка перетинає основу картини в
точці
![]() ,
предметну площину по прямій
,
предметну площину по прямій
![]() (предметний слід площини), картинну
площину по прямій
(предметний слід площини), картинну
площину по прямій
![]() (картинний слід площини), які
мають спільну точку
.
Пряма
(картинний слід площини), які
мають спільну точку
.
Пряма
![]() - горизонтальна пряма предметної
площини, для побудови перспективи якої
досить встановити її граничну точку
- горизонтальна пряма предметної
площини, для побудови перспективи якої
досить встановити її граничну точку
![]() .
Пряма
.
Пряма
![]() буде перспективою предметного
сліду площини
.
Картинний слід
буде перспективою предметного
сліду площини
.
Картинний слід
![]() площини
співпадає зі своїм перспективним
зображенням
.
На картині відрізок
площини
співпадає зі своїм перспективним
зображенням
.
На картині відрізок
![]() ,
який є зображенням предметного сліду
площини, завжди обмежений двома
точками. Картинний же слід
площини, при потребі, може бути
продовжений в кожному з напрямків
до нескінченності.
,
який є зображенням предметного сліду
площини, завжди обмежений двома
точками. Картинний же слід
площини, при потребі, може бути
продовжений в кожному з напрямків
до нескінченності.
Як горизонтальна пряма предметної
площини, так і прямі загального
розміщення, обмежені на картині
граничною точкою (Рис. 14, б, Рис. 36).
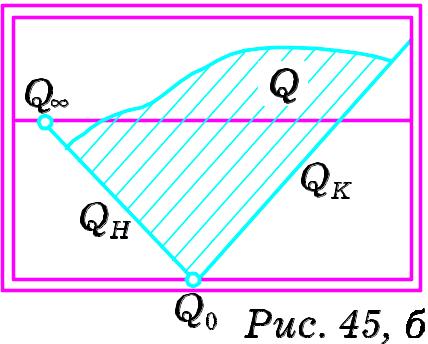
Так само площина в перспективі обмежена
граничною прямою. На картині (Рис.45, б)
зображено частину площини
,
обмежену хвилястою лінією. Для побудови
більш наочного зображення площини,
побудуємо на картині граничну пряму
площини
![]() .
.
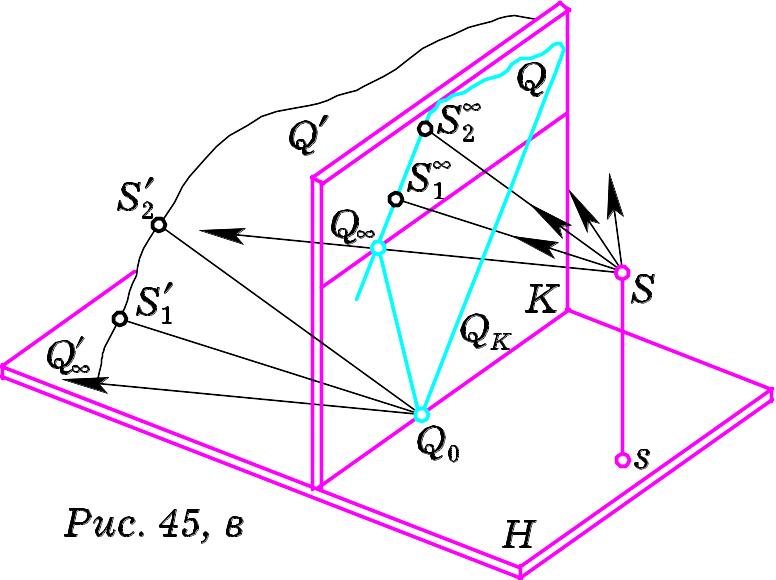
Перспектива кожної з прямих
![]() ,
,
![]() ,
,
![]() ,
… ,
,
… ,
![]() … , які лежать в площині
,
матиме граничну точку
,
… , які лежать в площині
,
матиме граничну точку
,
![]() ,
,
![]() ,
… ,
,
… ,
![]() відповідно. Кожен з променів зору
відповідно. Кожен з променів зору
![]() ,
,
![]() ,
,
![]() ,
… ,
,
… ,
![]() ,
… буде паралельним до о
,
… буде паралельним до о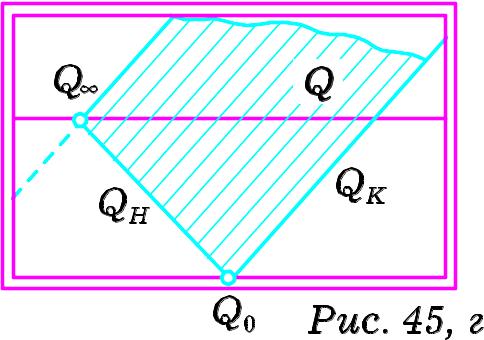 днієї
з прямих
днієї
з прямих
![]() ,
,
,
… ,
… площини
.
Тому такими променями зору утвориться
площина
,
,
,
… ,
… площини
.
Тому такими променями зору утвориться
площина
![]() ,
паралельна до площини
.
Площина
перетне картину по прямій, паралельній
до
.
Очевидно, що вказана пряма пройде через
точку
.
Отже, для побудови граничної прямої
площини загального розміщення досить
через граничну точку
її предметного сліду в площині картини
провести пряму, паралельну до картинного
сліду площини.
,
паралельна до площини
.
Площина
перетне картину по прямій, паралельній
до
.
Очевидно, що вказана пряма пройде через
точку
.
Отже, для побудови граничної прямої
площини загального розміщення досить
через граничну точку
її предметного сліду в площині картини
провести пряму, паралельну до картинного
сліду площини.
Довільна пряма, що належить площині в перспективі матиме свою граничну точку на граничній прямій площини .
Площину на картині можна задати граничною прямою та картинним слідом. Для побудови предметного сліду такої площини досить з’єднати точку перетину картинного сліду площини і основи картини з точкою перетину граничної прямої площини і лінії горизонту картини.
Якщо площина перпендикулярна або паралельна до картинної або предметної площини, то її називають площиною часткового розміщення.
Н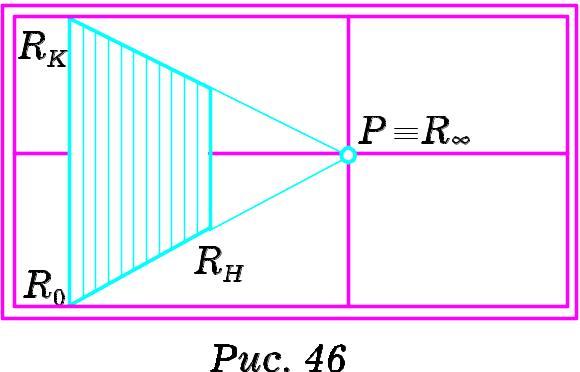 а
картині (Рис. 46) зображено перспективу
а
картині (Рис. 46) зображено перспективу
![]() площини
площини
![]() ,
перпендикулярної до предметної та
картинної площин. Її називають глибинною.
Положення глибинної площини на картині
визначається такими ознаками:
,
перпендикулярної до предметної та
картинної площин. Її називають глибинною.
Положення глибинної площини на картині
визначається такими ознаками:
картинний слід
 перпендикулярний до основи картини;
перпендикулярний до основи картини;граничною точкою
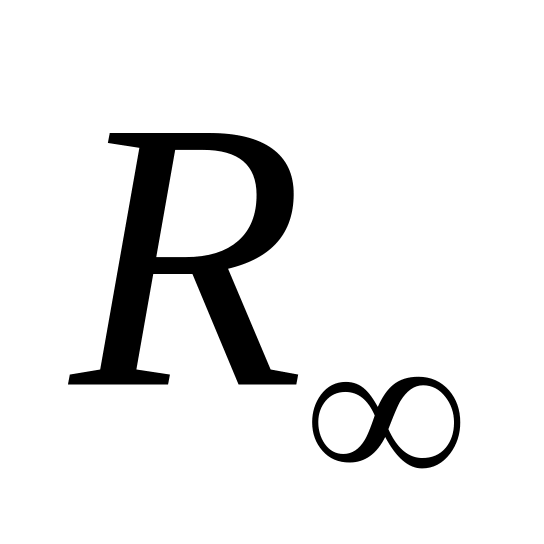 предметного сліду RH
площини є головна
точка картини P;
предметного сліду RH
площини є головна
точка картини P;граничною прямою глибинної площини буде лінія головного вертикалу.
Я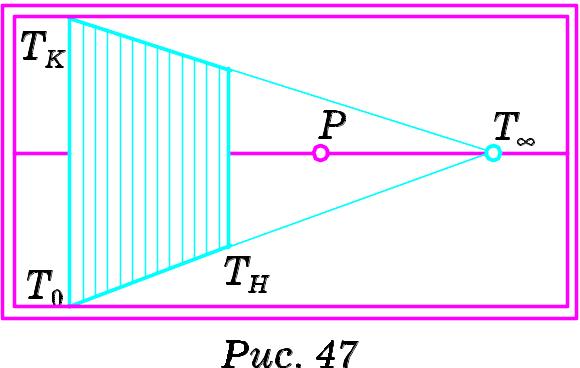 кщо
глибинна площина проходить через
головний промінь зору, то її перспективою
буде лінія головного вертикалу.
кщо
глибинна площина проходить через
головний промінь зору, то її перспективою
буде лінія головного вертикалу.
На картині (Рис. 47) зображено перспективу
![]() площини
площини
![]() ,
перпендикулярної до предметної площини
і не перпендикулярної
до картини. ЇЇ називають проеціюючою.
Положення проеціюючої
площини на картині визначають такими
ознаками:
,
перпендикулярної до предметної площини
і не перпендикулярної
до картини. ЇЇ називають проеціюючою.
Положення проеціюючої
площини на картині визначають такими
ознаками:
картинний слід
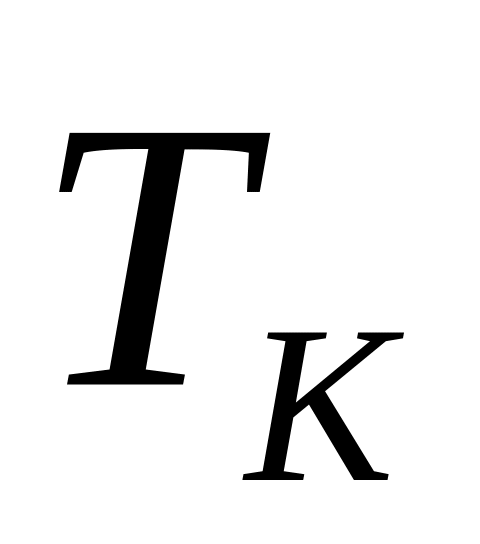 перпендикулярний
до основи картини;
перпендикулярний
до основи картини;граничною точкою
 предметного сліду
предметного сліду
 площини є довільна точка лінії горизонту,
відмінна від головної;
площини є довільна точка лінії горизонту,
відмінна від головної;граничною прямою проеціюючої площини буде пряма, що проходить через граничну точку предметного сліду площини перпендикулярно до лінії горизонту.
Н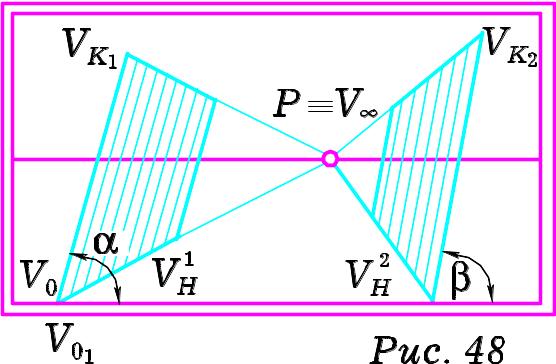 а
картині (Рис. 48) зображено перспективи
а
картині (Рис. 48) зображено перспективи
![]() та
та
![]() площин
площин
![]() та
та
![]() ,
кожна з яких перпендикулярна до картини
і утворює різні двогранні кути з
предметною площиною. Ці площини також
називають проеціюючими. Їх положення
на картині визначається такими ознаками:
,
кожна з яких перпендикулярна до картини
і утворює різні двогранні кути з
предметною площиною. Ці площини також
називають проеціюючими. Їх положення
на картині визначається такими ознаками:
граничною точкою
 предметних слідів
предметних слідів
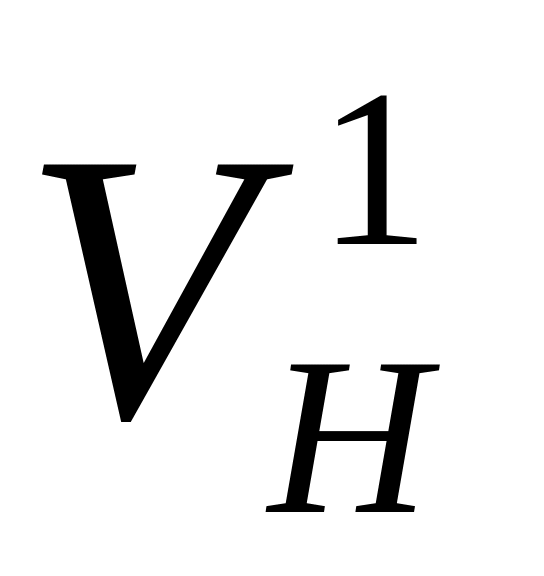 та
та
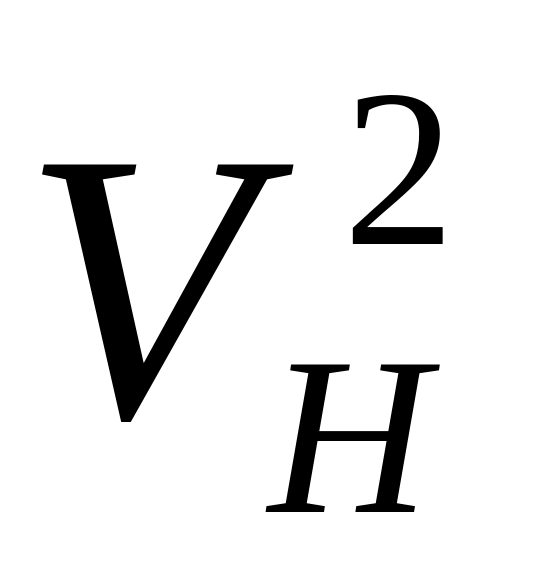 є головна точка картини;
є головна точка картини;
кути нахилу картинних слідів цих проеціюючих площин до основи картини в дійсності дорівнюють двогранним кутам, які площини та утворюють з предметною площиною;
граничні прямі площин та пройдуть через головну точку картини і будуть паралельними до своїх картинних слідів;
кутом між проеціюючими площинами вказаного розміщення буде кут між їх граничними прямими.
На картині (Рис. 49) зображено перспективу
![]() площини
площини
![]() ,
перпендикулярної до предметної площини
і паралельної до картини. Таку площину
називають фронтальною. ЇЇ
положення та властивості на картині
визначаються такими характеристиками:
,
перпендикулярної до предметної площини
і паралельної до картини. Таку площину
називають фронтальною. ЇЇ
положення та властивості на картині
визначаються такими характеристиками:
п
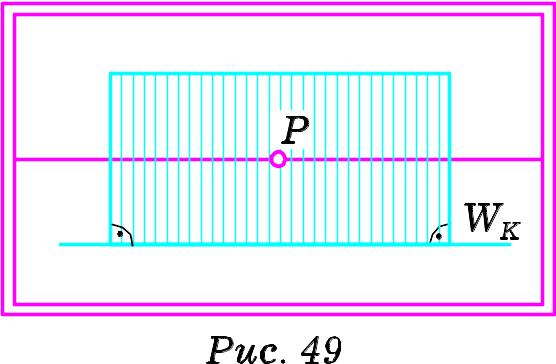 редметний
слід
редметний
слід
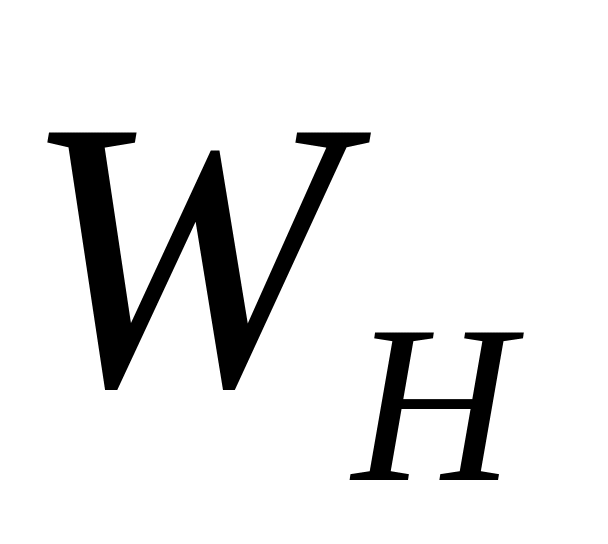 паралельний до основи картини;
паралельний до основи картини;величини усіх кутів, які в дійсності розташовані у фронтальній площині, зображаються в перспективі без спотворень;
к
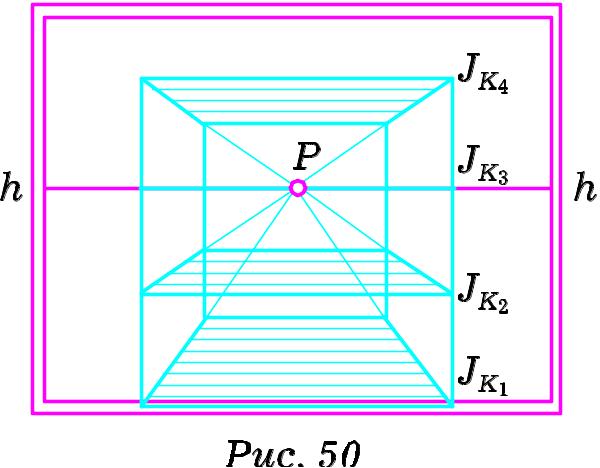 артинного
сліду площина не має.
артинного
сліду площина не має.
На картині (Рис. 50) зображено перспективи
![]() ,
,
![]() ,
,
![]() ,
,
![]() площин
площин
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
кожна з яких паралельна до предметної
площини, а отже перпендикулярна до
картини. Такі площини називають
горизонтальними. Їх положення
на картині визначається такими ознаками:
,
кожна з яких паралельна до предметної
площини, а отже перпендикулярна до
картини. Такі площини називають
горизонтальними. Їх положення
на картині визначається такими ознаками:
картинні сліди
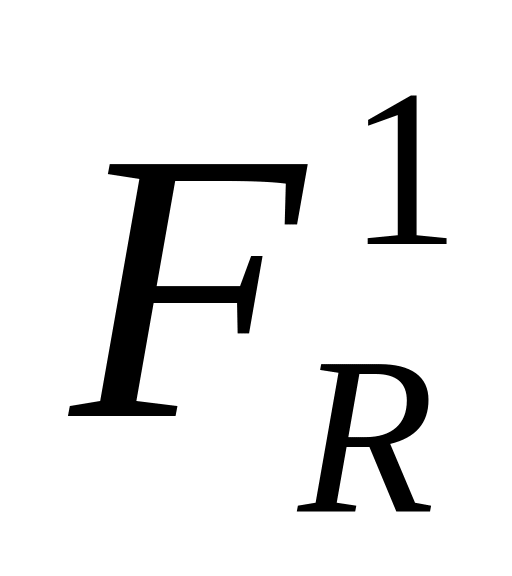 ,
,
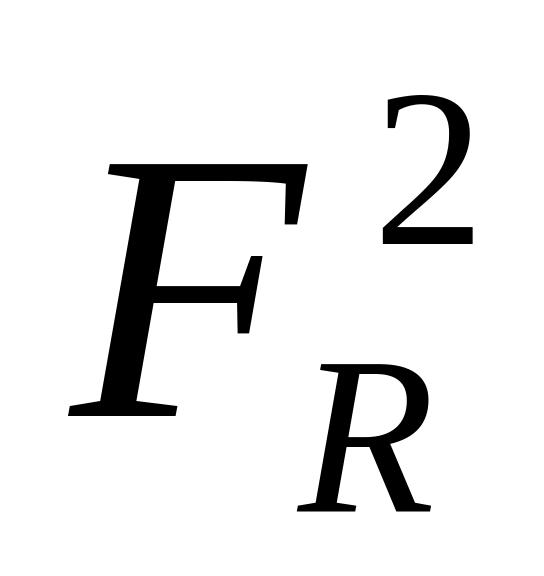 ,
,
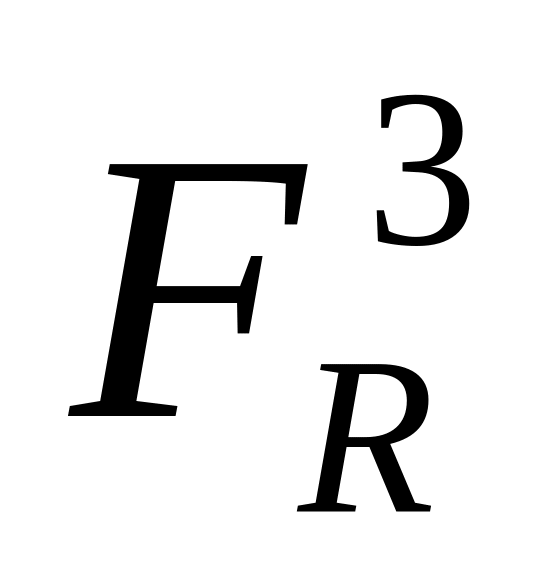 ,
,
 горизонтальних площин паралельні
до основи картини;
горизонтальних площин паралельні
до основи картини;граничною прямою горизонтальних площин є лінія горизонту картини;
предметного сліду горизонтальні площини не мають.
Я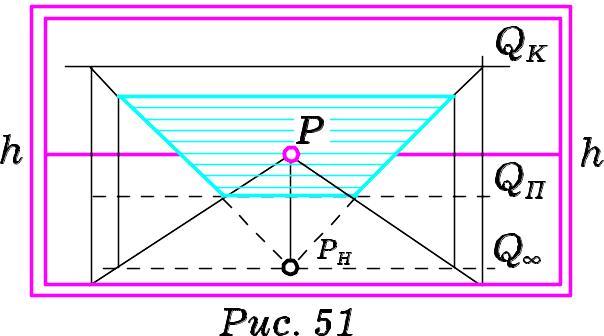
 кщо
горизонтальна площина
проходить через головний промінь зору,
то її картинний слід
співпадає з лінією горизонту. Таке
зображення горизонтальної площини на
картині не наочне, тому для розв’язування
задач на побудову його не використовують.
кщо
горизонтальна площина
проходить через головний промінь зору,
то її картинний слід
співпадає з лінією горизонту. Таке
зображення горизонтальної площини на
картині не наочне, тому для розв’язування
задач на побудову його не використовують.
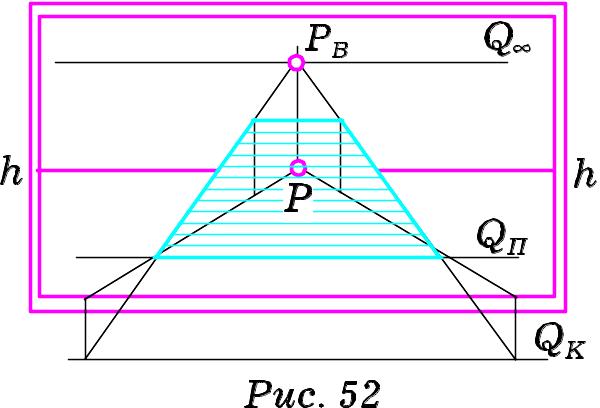
На картинах (Рис. 51 та Рис. 52) зображено площини, паралельні до основи картини. При цьому кути, які вони утворюють з предметною та картинною площинами, можуть бути довільними. Положення таких площин називають особливим. Площина особливого розміщення може бути нисхідною (Рис. 51) або висхідною (Рис. 52). Нисхідна площина напрямлена від глядача згори донизу. Висхідна площина напрямлена від глядача знизу доверху.
