§6. Взаємне розташування прямих

При створенні художніх зображень найчастіше доводиться мати справу з паралельними прямими. В геометрії множину усіх прямих, паралельних до заданої, називають в’язкою прямих. Якщо прямі непаралельні, то вони або перетинаються, або мимобіжні. Важливо знати та уміти визначати ознаки взаємного розташування двох прямих на картині. Це дасть можливість розв’язувати прямі (будувати перспективу взаємного розташування прямих) і обернені (визначати їх взаємне розташування по зображенню на картині) задачі.

Паралельні прямі. На Рис. 12, б прямі , , , утворюють в’язку прямих, паралельних до головного променя зору. Нагадаємо, що точкою сходу глибинних прямих буде головна точка картини, тобто точка Р – центр пучка прямих, кожна з яких є перспективою однієї з глибинних прямих (Рис. 13). Більше того, головна точка картини буде зображенням прямої .

На Рис. 14, а прямі , , , утворюють в’язку горизон­таль­них прямих, не перпендику­лярних до пло­щини картини. Їх перспективою будуть прямі , , пучка прямих картинної площини, що проходять через точку сходу вказаних прямих. При цьому перспективою прямої буде точка (Рис. 14, б).

Якщо на картині зображено підлогу, на якій є квадратні елементи і при цьому сторона кожного з квадратів паралельна до основи картини, то для діагоналей усіх таких квадратів дистанційні точки картини будуть точками сходу.

З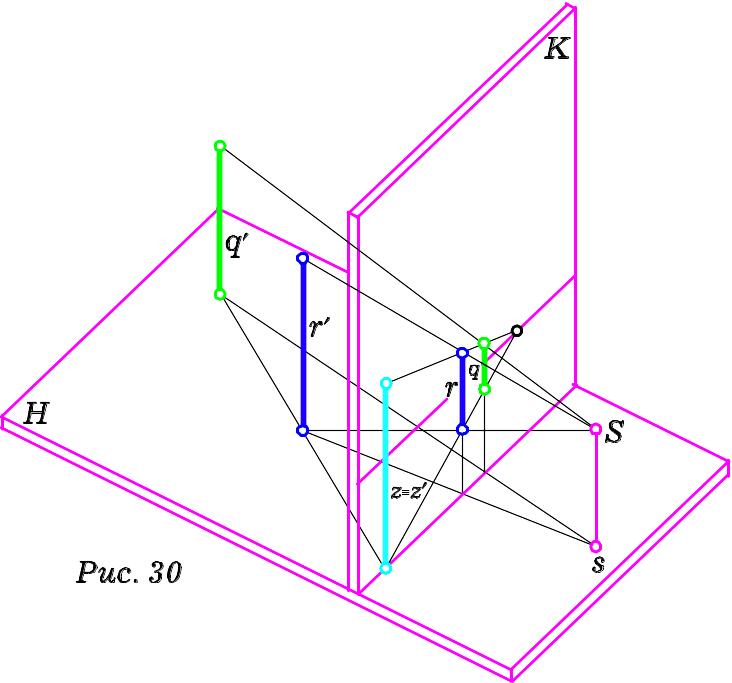 рисунків 16, а та 16, б робимо висновок, що зображенням в’язки вертикальних прямих будуть вертикальні прямі картини.

На Рис. 30 відрізки z, r, q розташовані на одній прямій і мають однакову «висоту». Такий випадок взаємного розташування вер­тикальних прямих досить часто зустрі­ча­ється на практиці. Перспективне зобра­ження вказаних відрізків зрозуміле, якщо пригадати усе, що ми вивчали досі.

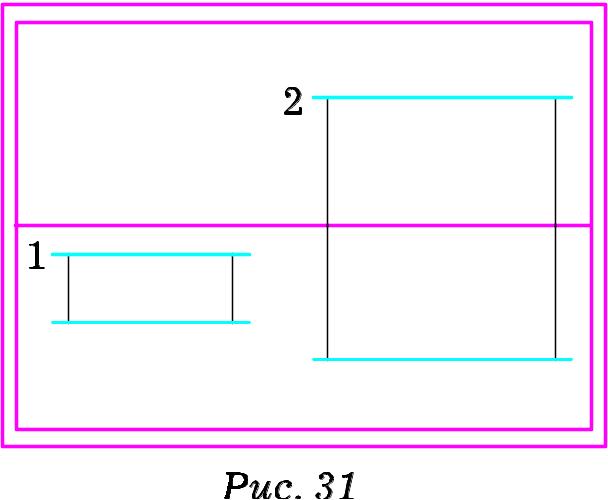
На Рис. 31 зображено горизонтальні прямі 1 та 2, кожна з яких паралельна як до предметної площини, так і до картини. Як перспективи самих прямих, так і перспективи їх проекцій паралельні до лінії горизонту.

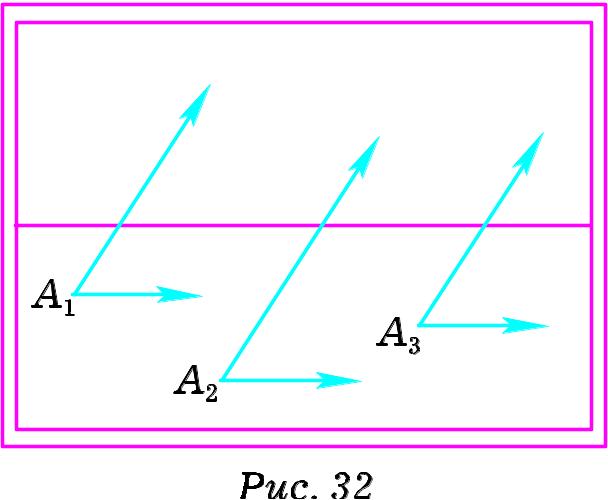
На картині (Рис. 32) А₁, А₂ та А₃ – паралельні між собою фронтальні прямі. В перспективі фронтальні прямі паралельні між собою, а їх проекції паралельні до основи картини, оскільки не мають граничних точок.

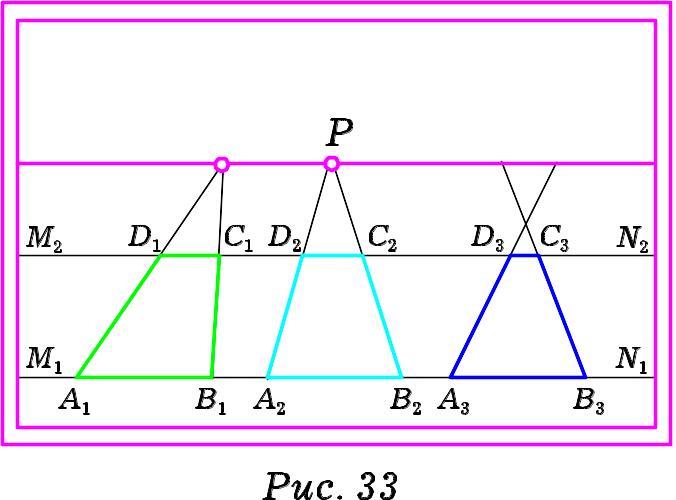
На картині (Рис. 33) в предметній площині зображено прямі M₁N₁ та M₂N₂, кожна з яких пара­лельна до основи картини. Це означає, що прямі та предметної площини, зо­бра­женням яких є прямі та , паралельні між собою і пара­ле­льні до основи картини. В площині картини проведемо через точки А₁ та В₁, А₂ та В₂ прямі так, щоб A₂D₂ та B₂C₂ перетиналися в головній точці картини, а A₁D₁ та D₁C₁ – в довільній точці лінії горизонту, відмінній від головної. Тоді чотирикутники A₁В₁C₁D₁ та A₂В₂C₂D₂ – перспективи паралелограмів. Більше того, A₂В₂C₂D₂ – прямокутника. Чотирикутник A₃В₃C₃D₃, у якого продовження сторін A₃D₃ та В₃C₃ перетинаються в точці, що не лежить на лінії горизонту, буде зображенням трапеції.

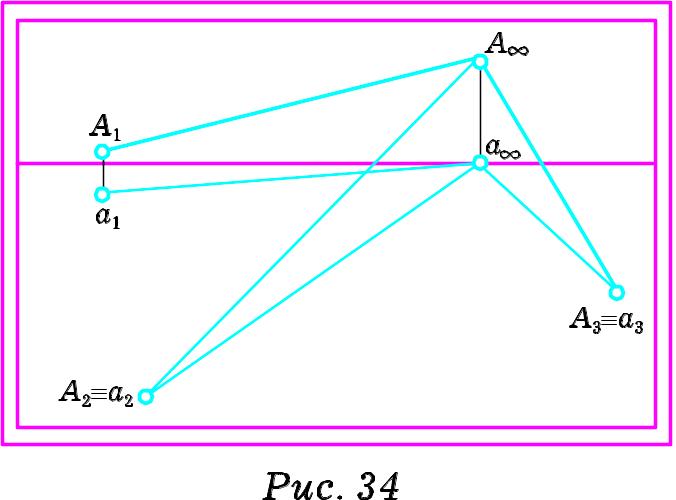
Р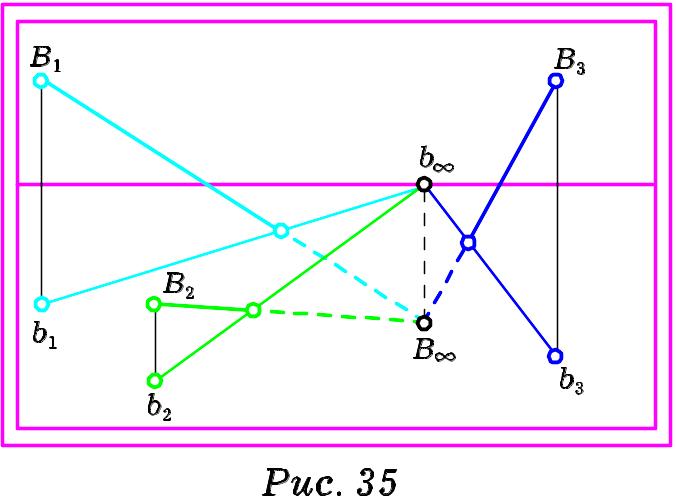 озглянемо перспективу висхідних паралель­них прямих загального розміщення (Рис. 34). Оскільки вис­хідні прямі , , паралельні, то паралельними бу­дуть їх проекції , , на предметну площину. Перс­пективи паралельних прямих, що лежать в пред­метній площині, матимуть спільну точку сходу на лінії горизонту, відмінну від головної точки картини. Тоді точка сходу перспектив висхідних паралельних прямих загального розміщення лежатиме на перпен­дикулярі, проведеному до лінії горизонту через точку сходу перспектив їх проекцій і розташована над лінією горизонту.

Аналогічно будують зображення паралельних нисхідних прямих загального розміщення (Рис.35). Від­­різ­­няються зображення лише тим, що точка сходу перспектив нисхідних прямих буде розташована під лі­нією горизонту.

Т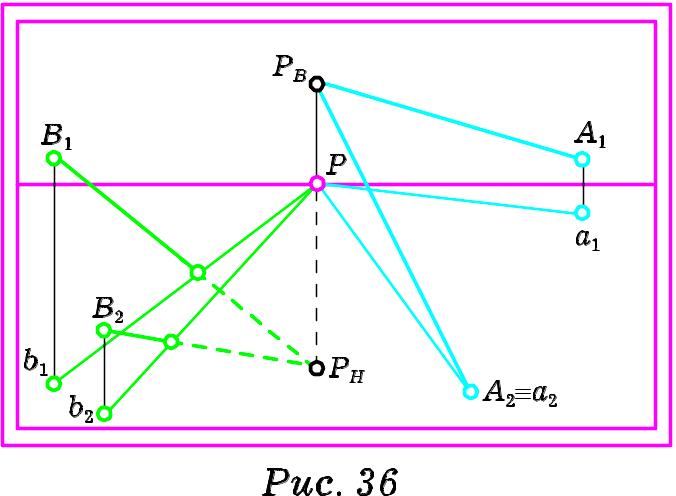 аким чином, ознакою паралельності прямих загального розміщення, зображених на картині, є розташування точок сходу прямих та їх проекцій на одному перпендикулярі. При цьому точка сходу перспектив проекцій прямих лежить на лінії горизонту.

На Рис. 36 зображено дві пари висхідних (А₁Р_В та А₂Р_В) і нисхідних (В₁Р_Н та В₂Р_Н) паралельних прямих особливого розміщення. Точкою сходу перспектив проекцій вказаних прямих буде головна точка картини. Точка сходу Р_В перспектив висхідних прямих і точка сходу Р_Н перспектив нисхідних прямих лежатимуть на лінії головного вертикалу.

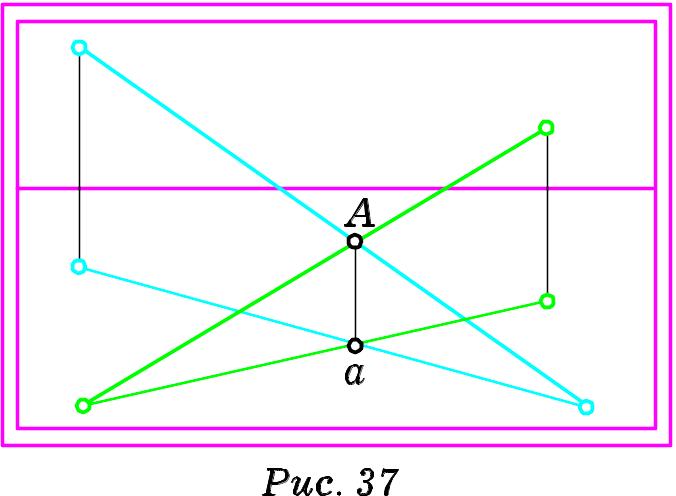
Прямі, що перетинаються. На картині (Рис. 37) задано дві прямі, що перетинаються в точці А. Тоді а, точ­ка перетину їх проекцій, лежатиме на одній вер­тикальній прямій з точкою А. Отже, якщо на картині точки А та а розташовані на одній вертикальній прямій, то в дійсності прямі перетинаються.

М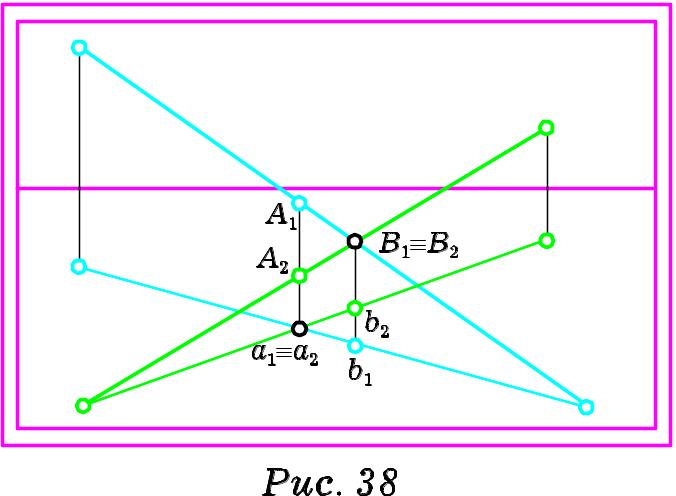 имобіжні прямі. Нагадаємо, що мимо­біж­ни­ми називаються прямі, які не мають спільної точки і не паралельні. Тому на картині (Рис. 38) точки перетину прямих і їх проекцій не повинні лежати на одній вер­тикальній прямій. Отже, якщо вертикальна пряма на картині, проведена через точку перетину проекцій двох прямих, перетинає ці прямі в двох різних точках А₁ та А₂, то дані прямі в дійсності мимобіжні. На картині точка, яка здається перетином двох прямих, є зображенням двох різних точок В₁ та В₂, що лежать на мимобіжних прямих. В дійсності точки та лежать на одному промені зору.

Основа b₁ точки В₁ розташована ближче від основи картини, ніж точка b₂, яка є основою точки В₂. Це означає, що в дійсності в предметному просторі точка розташована ближче від картини, ніж точка .