§4 Перспектива прямих часткового та особливого розміщення

Розташування прямих відносно проекційного апарату також може бути різним. Якщо прямі лежать у предметній площині або до неї паралельні, то такі прямі називають гори­зо­н­­тальними. В свою чергу, відносно картинної площини горизонтальні прямі мо­жуть бути паралельними, перпендикулярними або утворювати з нею довільний кут.

Якщо пряма перпендикулярна до предметної площини, а отже, пара­лель­на до картини, то її називають вертикальною.

Я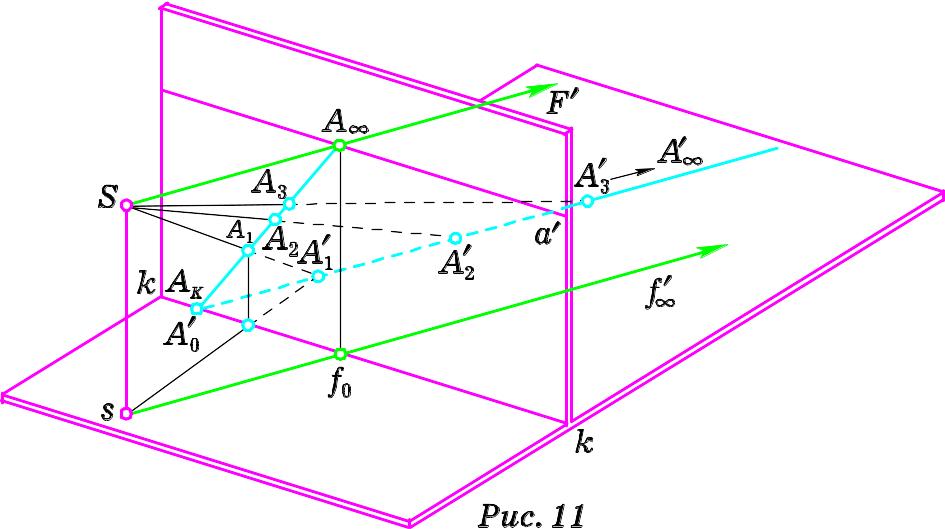 кщо пряма паралельна до пло­щини картини але нахилена до пред­метної площини під до­ві­ль­ним ку­том, то її називають фрон­тальною.

Горизонтальні, вертикальні та фрон­тальні прямі називають пря­ми­ми часткового розмі­щен­ня.

Може трапитися, що пряма ут­во­рює з предметною та картин­ною пло­щинами довільні кути, але при цьо­му лежати в площині, пер­пен­ди­кулярній до картинної пло­щини. Такі прямі називають прямими особливого розміщення. Зауважимо, що площина, яка міс­тить пряму особливого розміщення, паралельна до площини головного променя зору sSp, або співпадає з нею. (Д О Д А Т И Р И С У Н О К)

Почнемо вивчення методів побудови перспективних зображень прямих саме з прямих часткового та особливого розміщення.

1. Побудуємо перспективу a горизонтальної прямої , яка ле­жить у предметній площині і утво­рює з основою kk картини кут, від­мін­ний від прямого (Рис. 11). Зафі­к­суємо точку перетину прямої з картинною площиною. Точка буде картин­ним слідом A₀ пря­мої , до того ж . Для побудови пер­спек­тиви прямої досить в кар­тин­ній площині побудувати зобра­жен­ня ще однієї точки прямої . З цією метою на прямій зафіксуємо точку і побудуємо її перспективу способом, що описано у попе­редньому параграфі. Точками A₀ та в картинній площині визначається пряма , яка є перспективою прямої .

Будемо віддаляти точку , рухаючи її вздовж прямої , в положення , , … . Тоді точка на картині буде переміщуватися уздовж прямої , займаючи відповідно по­ложення , , … . При цьому кут між прямою sS та променями зору , , , … буде збільшуватися, прямуючи до . Промінь зору , проведений в нескінченно віддалену точку стане паралельним до прямої , а отже і до предметної площини, і перетне площину картини в точці . Вказана точка являє собою перспективу не скін­чено від­да­леної точки прямої . Отже при побудові перспективи прямої потрібно врахувати, що промінь проводиться лише до точки . Точку називають граничною точкою прямої .

Встановимо як отримати точку в картинній площині. Площина паралельна до прямої , оскільки прямі та паралельні. Тому лінія перетину площин та H – паралельна до . Точка лежить в площині картини на перпендикулярі m, проведеному до основи картини kk. Довжини відрізків f₀A_∞, та sS рівні. Звідси робимо висновок, що гранична точка прямої лежить на лінії горизонту.

З проведених міркувань випливає правило побудови перспективи горизонтальної прямої предметної площини:

1) через точку s проводимо пряму, паралельну до ;

2) знаходимо точку перетину прямих kk та ;

3) через точку в площині картини проводимо пряму m, перпендикулярну до kk;

4) точку одержуємо від перетину прямих hh та m;

5) відрізок А_КА_∞ картинної площини буде шуканою перспективою прямої .

Б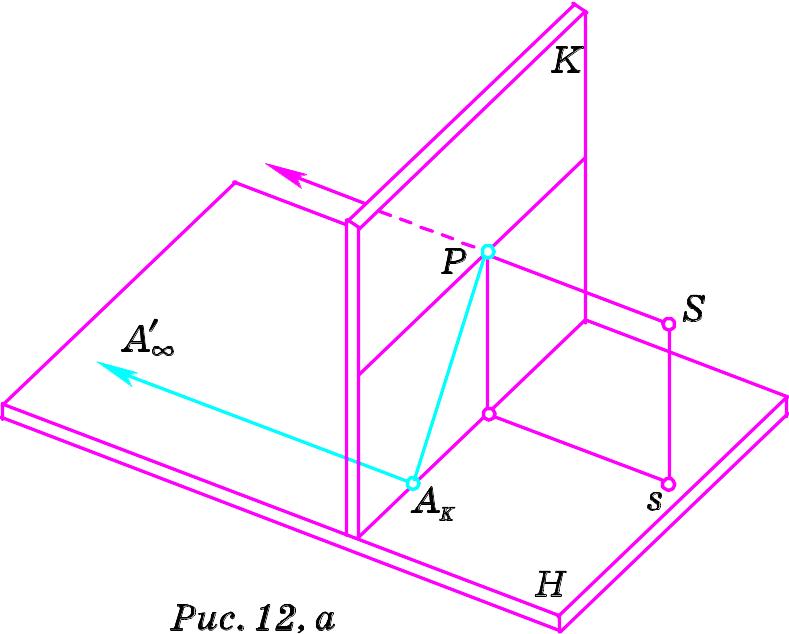 удь-яка інша пряма предметної площини, паралельна до , матиме граничною точку .

2. Розглянемо горизонтальну пряму , яка лежить в предметній площині і перпен­ди­ку­лярна до площини картини (Рис. 12, а). По­бу­ду­ємо перспективу цієї прямої. Картинний слід прямої відомий. Тому для здійснення по­тріб­ної побудови досить знайти граничну точку. Оскіль­ки головний промінь зору пара­лель­ний до пря­­мої , то гранична точка та­кої прямої спів­падає з головною точкою кар­ти­ни.

Отже, гранична точка горизонтальної прямої, яка лежить в предметній площині і перпендикулярна до площини картини, спів­падає з головною точкою картини (закон головної точки).

З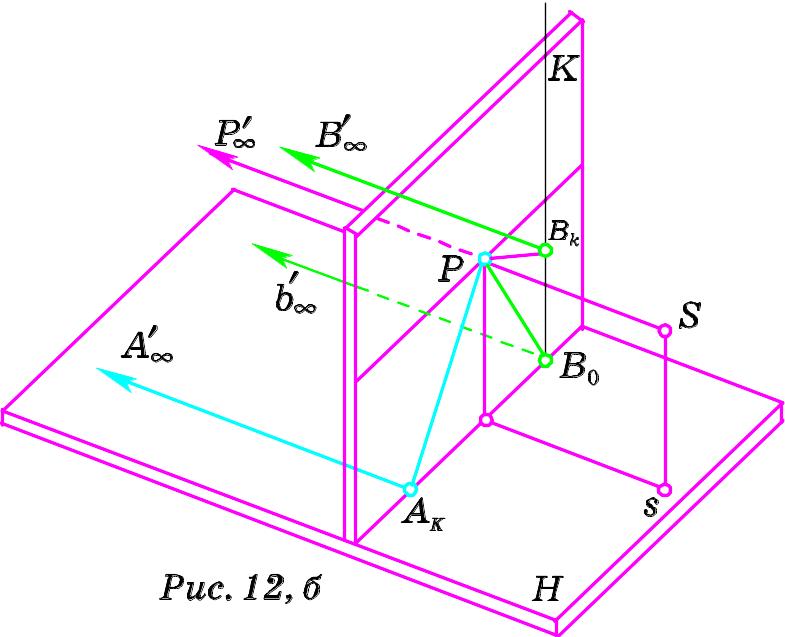 акон головної точки має місце для довіль­ної іншої прямої предметної площини вказаного розміщення. Тому усі прямі предметної пло­щи­ни, перпендикулярні до кар­тин­ної площини, ма­ють спільну граничну точку Р.

Розглянемо пряму перпендикулярну до картинної площини і паралельну до пред­мет­ної площини (Рис. 12, б). Нехай - картинний слід вказаної прямої. Через точку в картин­ній пло­щині опустимо перпендикуляр на її основу kk. Пряма буде проекцією прямої на предметну площину. Побудуємо спочатку перс­пек­­ти­ву про­екції цієї прямої. Оскільки голо­в­ний промінь зору пара­лель­ний з прямою , то її граничною точкою також буде головна точка картини Р. Тому для побудови перс­пективи прямої досить сполу­чити кар­тинний слід цієї прямої з головною точкою картини (Рис. 13).

З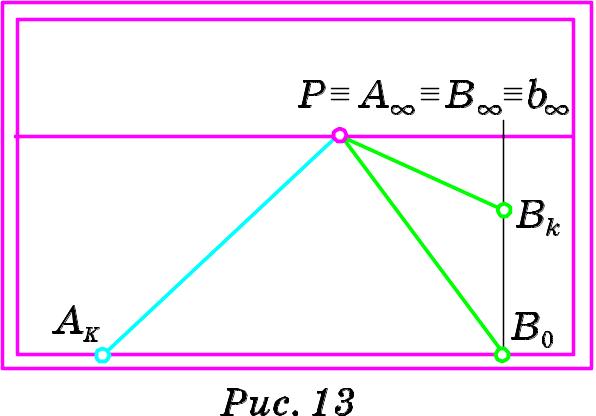 ауважимо, що пряму, паралельну до предметної пло­щини і перпендикулярну до картини, називають глибин­ною. Вона визначає один з головних напрямків картини – глибину виміру. Зокрема глибинною буде також пряма . Зверніть увагу (Рис. 13), що глибинна пряма має лише картинний слід.

В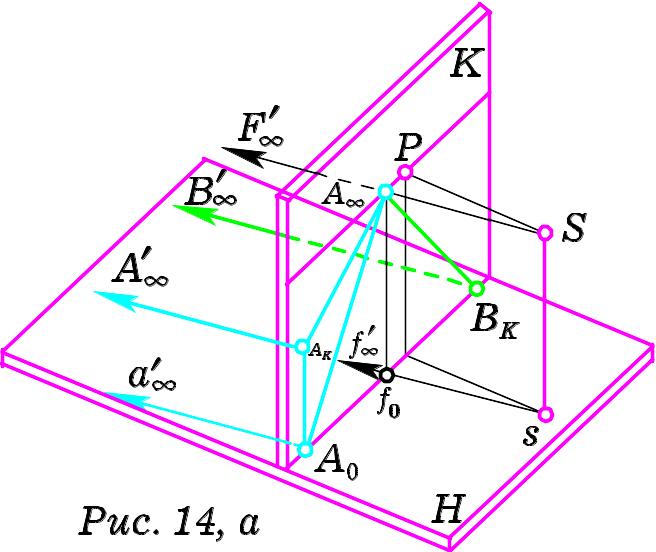 геометрії фігуру, що складається з усіх прямих пло­щи­ни, які проходять через певну її точку, називають пуч­ком прямих. Із проведених вище міркувань випливає, що усі глибинні прямі пред­метного про­с­­тору мають спільну граничну точку. Цю точку називають точкою сходу пара­лельних прямих. Тому перспективи усіх глибинних прямих утворять пучок прямих картинної площини з точкою сходу у головній точці картини, яка буде центром пучка.

3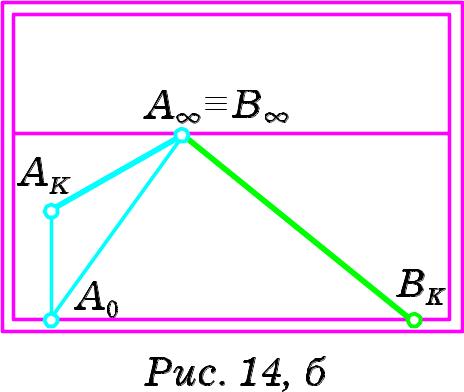 . Далі логічно розглянути горизонтальну пряму , пара­лельну до предметної пло­щини, розташовану до картинної площини під довільним кутом (Рис. 14, а) і побудувати її перспективу. Нехай - картинний слід вказаної прямої. Через точку в картинній пло­щині проведемо перпен­дикуляр до її основи kk. Нехай пряма - проекція прямої на предметну площину. Побудову перспективи прямої ми розглянули в п. 1 цього параграфа. Тому почнемо побудову перспективи прямої з побудови перс­пек­тиви її проекції на предметну площину. В предметній площині проведемо пряму паралельну до до перетину з основою картини kk. Якщо - точка їх перетину, то для побудови граничної точки прямої досить в площині картини провести вертикальну (перпендикулярну до kk) пряму до перетину з лінією горизонту. Картинний слід прямої відомий. З побудови прямої випливає що вона пара­лельна до прямої . Оскільки прямі та також паралельні то , а от­же точка є граничною для пря­мої .

Із проведених міркувань робимо висновок, що горизон­та­льна пряма, що паралельна до предметної площини і утворює з картиною дові­льний кут, в перспективі має граничну точку на лінії горизонту. Ця точка відмінна від головної. Пряма та її проекція на предметну площину мають спільну граничну точку.

Зверніть увагу (Рис. 14, б), що горизонтальна пряма , розташована під довіль­ним кутом до площини картини, має лише картинний слід.

О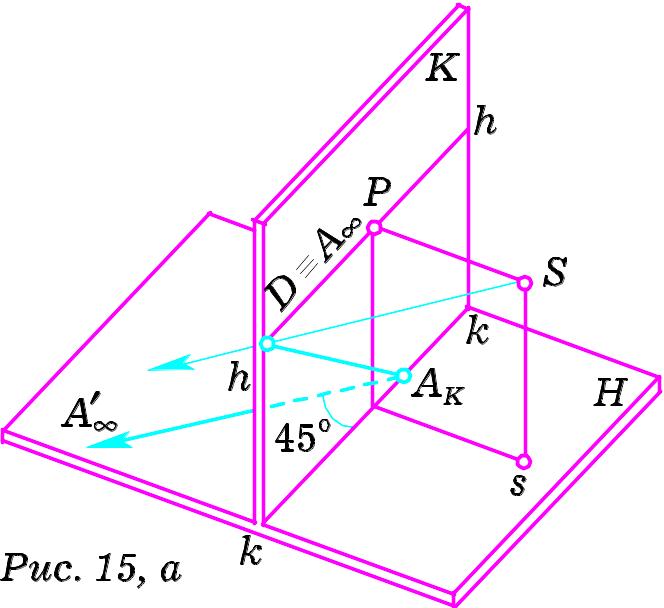 скільки усі горизонтальні прямі , що паралельні між собою і не перпендикулярні до площини картини, мають спільну граничну точку, то ця точка на лінії горизонту картини буде їх спільною точкою сходу. При цьому точка сходу не співпадає з головною точкою картини.

Розглянемо частковий випадок горизонтальних пря­мих вказаного вище розміщення, який часто зустрі­чається на практиці. Встановимо граничну точку прямих, кут між якими і картинною площиною становить 45°. Нехай (Рис. 15, а) така пряма. Промінь зору, паралельний до неї, перетне картинну площину в дис­танційній точці D. Дійсно, гострий кут прямокутного трикутника SPD дорівнює 45°. Тому його катети рівні і точка D розташована на лінії горизонту на відстані PD, рівній довжині головного променя зору. Тоді точ­ка D є дистанційною за озна­ченням.

Т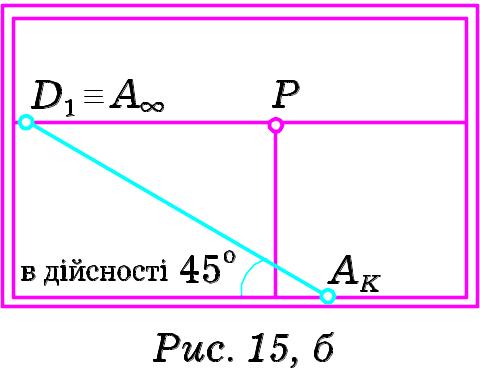 аким чином, якщо на кар­тині потрібно зобразити горизонтальну пря­му, кут між якою і картинною площиною дорівнює 45°, то для цього досить знайти її кар­тин­ний слід і сполучити його з потрібною дистанційною точкою (Рис. 15, б).

Н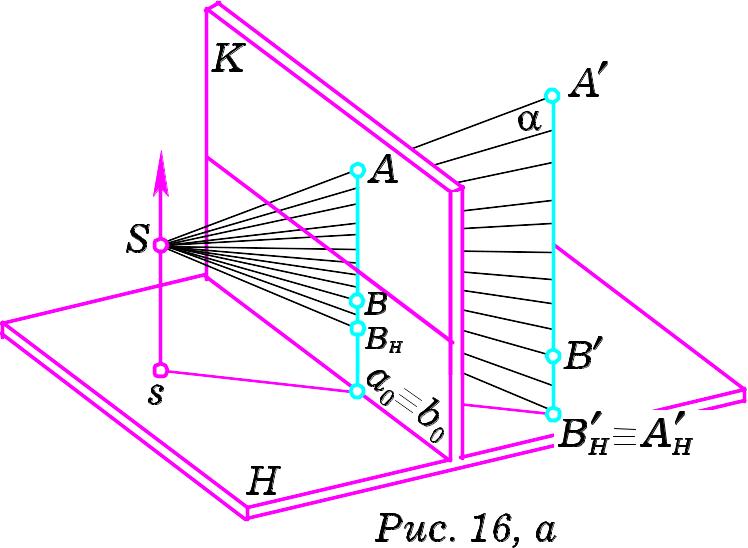 агадаємо, що дистанційна точка не обов’язково розташо­вана в межах картини.

4. Розглянемо прямі, перпен­ди­кулярні до пред­метної площини, а отже паралельні до пло­­щини кар­тини. Їх назива­ють вертикальними. Задамо в пред­метному просторі від­різок A´B´ вертикальної прямої та побудуємо перспек­тиву цієї прямої (Рис. 16, а).

До точок A´ та B´ прямої проведемо промені зо­ру і знайдемо точки їх перетину A та B з картинною пло­щиною. Перспективою прямої A´B´ буде пряма, проведена через точки A та B. Пряма AB є лінією пер­етину картини з площи­ною α, утвореною проме­нями зору, проведеними до кожної точки прямої A´B´ . Оскільки пряма A´B´ перпендикулярна до предметної площини, то площина α також буде до неї перпен­ди­кулярною. Тому пряма AB , яка є лінією перетину пло­щин α та K, перпендикулярна до предметної пло­щини, а отже і до основи картини kk.

І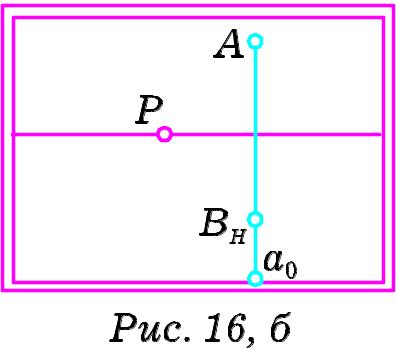 з проведених міркувань випливає, що зображення верти­кальної прямої на картині (Рис. 16, б) розташовано перпен­дикулярно до основи картини і не має граничної точки. Дійсно, про­мінь зору SS_∞, напрямлений в нескінченно віддалену точку A´_∞ прямої A´B´, буде паралельним до площини картини, а отже не матиме з нею спільної точки.

Нехай – проекція точки A´, - проекція точки B´ на пред­метну площину. Тоді точки та співпадають і кожна з них є предметним слідом прямої A´B´.

Пряма – лінія перетину предметної площини з площиною α. Якщо прямі kk та перетинаються в точці , то - перспективне зображення предметного сліду прямої AB. Із сказаного випливає спосіб побудови перспективи вертикальної прямої:

а) сполучаємо точку стояння s із предметним слідом вертикальної прямої;

б) знаходимо точку перетину побудованої прямої з основою картини;

в) пряма, проведена в площині картини через точку перпендикулярно до основи картини, буде перспективою заданої вертикальної прямої.

Вертикальна пряма визначає один з головних напрямків картини – висоту виміру.

5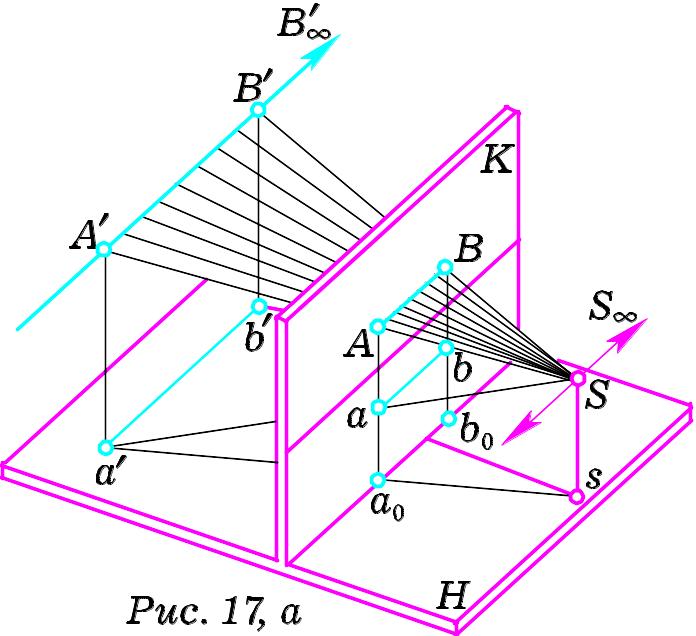 . Розглянемо нарешті горизонтальну пряму, роз­та­шовану в предметному просторі і паралельну як до пред­метної, так і до картинної площин. Тоді вона буде пара­лельною і до основи картини kk (Рис. 17, а). Нехай A´ та B´ - дві довільні точки вказаної прямої, a´ та b´ - проекції точок A´ та B´ на предметну площину. Прямі A´B´ та a´b´ паралельні. Паралельними будуть площина α, утво­рена прямими A´B´ та a´b´, і картинна площина K.

Побудуємо перспективу прямої . Промені зору, на­прямлені до кожної її точки, утворять площину A´SB´, яка перетне картину по прямій AB . Прямі A´B´ та AB паралельні як лінії перетину двох паралельних площин третьою. Так само будують перс­пек­тиву ab проекції a´b´ заданої прямої на предметну площину. Кожна з прямих AB та ab буде паралельною до основи картини kk. Промінь зору SS_∞, напрямлений в нескінченно віддалену точку B´_∞ прямої A´B´, буде паралельним до площини картини, а тому не матиме з нею спільної точки.

Отже, горизонтальна пряма, яка одночасно паралельна і до картинної, і до пред­метної площин, в перспективі розташована паралельно до основи картини, і гра­ничної точки не має.

Н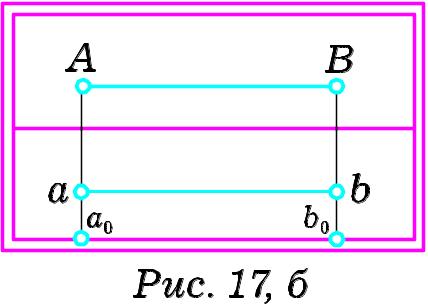 а Рис. 17, б зображено перспективу прямої A´B´ та її проекції a´b´. Відрізок є перспективою відстані від точки a´ до основи кар­тини. Відрізок Aa є перспективою висоти точки A´ над пред­метною площиною.

Зауважимо, що така пряма визначає один з головних напрямків картини – ширину виміру.

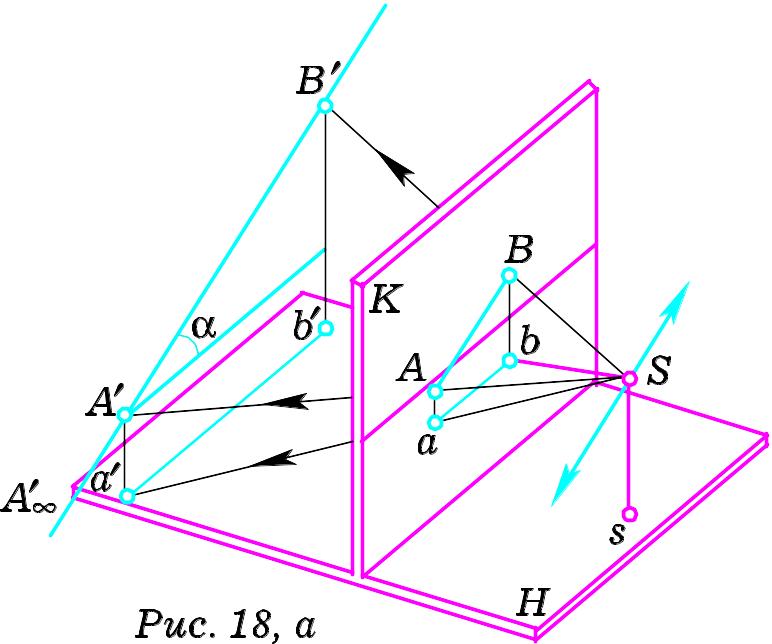
6. Прямі, паралельні до картини і нахилені під довільним кутом до предметної пло­щи­ни, нази­ва­ються фронтальними.

З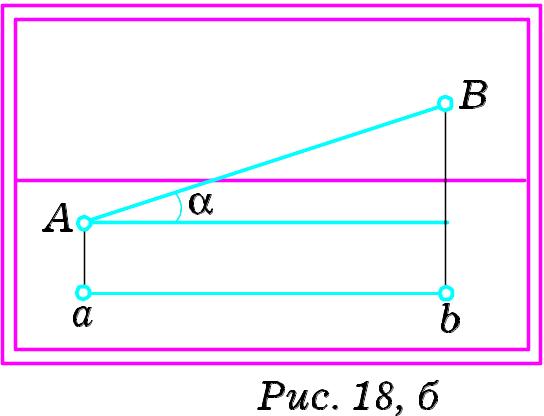 адамо в предметному просторі проекційного апарату відрізок A'B' фронтальної прямої (Рис. 18, а). Промені зору SA'_ та SB'_ будуть пара­ле­льними до прямої A'B', а отже і до площини картини. Тому фрон­тальна пряма не матиме граничної точки. Зау­ва­жимо, що проекція a'b' фронтальної прямої буде пара­лель­ною до основи картини. Тому перспек­тивне зобра­ження фрон­тальної пря­мої буде таким, як на Рис. 18, б. Більше того, перс­пективне зображення AB буде паралельним до самої прямої A'B'. Тому вели­чина кута, утвореного прямою A'B' з предметною площиною дорівнює величині кута між перс­пективою прямої AB та перспективою її проекції ab.

Перспектива фронтальної прямої не має граничної точки. Перспектива проекції фронтальної прямої пара­лельна до основи картини. Кут нахилу перспективи фрон­таль­ної прямої до основи картини (лінії горизонту) дорівнює куту нахилу фронтальної прямої до предметної площини.

На Рис. 18, а фронтальна пряма не має в ме­жах картини предмет­ного сліду. Побудову перспек­тиви вказаної прямої вико­ну­ють в такій послідов­но­сті:

1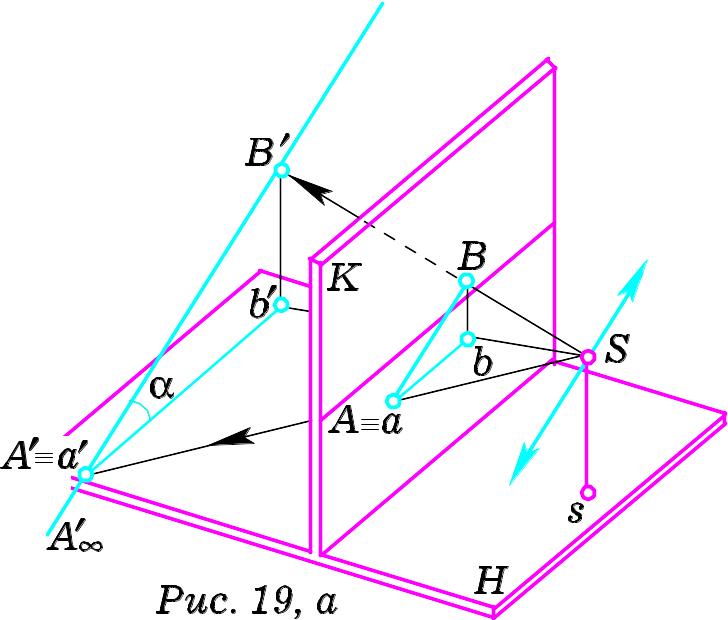 ) фіксують на пря­мій дві довільні точки разом з їх проекціями на предметну площину;

2) будують перспек­тиви вибраних точок;

3) сполучють попарно перспективи точок пря­мої та перспективи точок її проекції на фронтальну площину.

У випадку, який щойно розглянули, предмет­ний слід прямої A'B' одержимо від перетину прямих AB та ab. Очевидно, що він буде за межами картини.

Н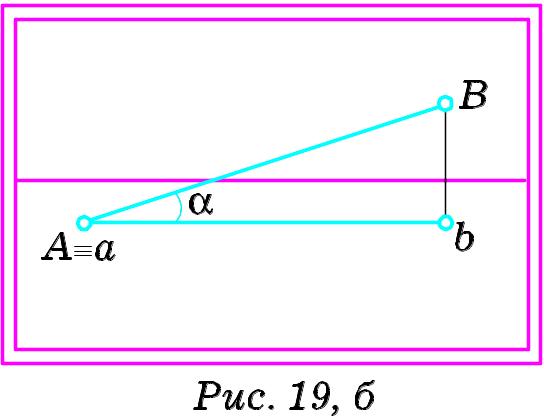 а Рис. 19 фрон­та­ль­на пряма має пред­мет­ний слід в межах карти­ни. Одна частина прямої (пра­­во­руч від предмет­но­го сліду) буде розташова­на над пред­метною пло­щи­ною. ЇЇ зображають су­ці­ль­ною лінією. Частину ж прямої, розта­шо­ва­ної під пред­метною площи­ною, зо­бражають штри­хо­вою лі­нією. Нижче ми переконаємося в необхідності виконання таких побудов.

7. Розглянемо прямі, які утворюють як з пред­метною, так і з картинною площинами довільні кути, але паралельні до площини основного променя зору. Їх називають прямими особливого розміщення. Проекції кожної з таких прямих на предметну площину будуть пер­пен­дикулярними до основи картини, а отже вони будуть глибин­ними прямими з граничною точкою P.

П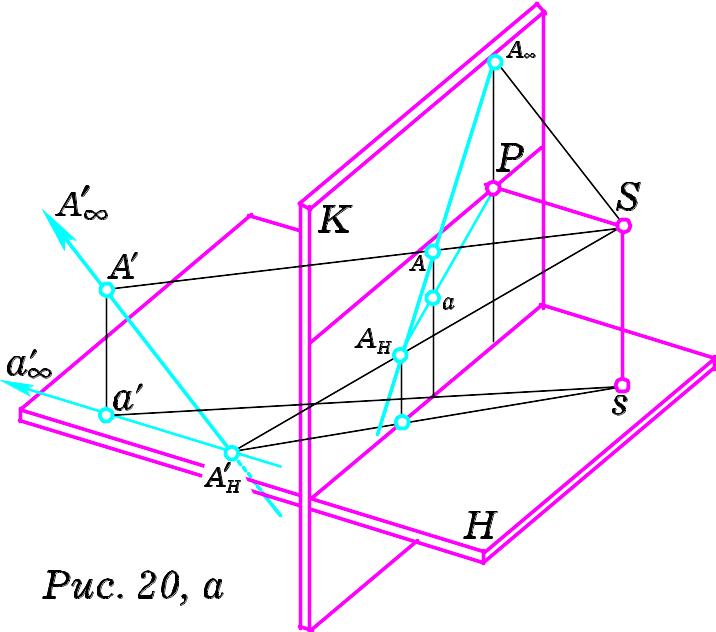 рямі особливого розміщення в залежності від напрямку можуть бути висхідними та нисхідними. Висхідною нази­вається така пряма, яка при віддаленні від глядача, напрямлена знизу догори. Нисхідною називається така пряма, яка при віддаленні від гля­дача, напрямлена зго­ри донизу.

На Рис. 20, а вис­хідна пряма пере­ти­­нає пред­метну пло­щи­ну в точці , яка є її пред­­мет­ним слідом. Пер­спек­тиву предмет­но­го сліду прямої бу­ду­­ємо так, як це було опи­сано в § 3. Пряма гори­зон­та­ль­­на пряма пре­д­метної пло­щини, пер­пен­дику­ляр­на до картини (глибинна пряма). ЇЇ граничною точ­кою (п.2, §4) буде головна точка картини. Тому промінь РА_Н буде перспективою проекції висхідної прямої .

Нехай тепер – довільна точка висхідної прямої особливого розміщення, – її проекція на предметну площину. Якщо А та а – перспективи вказаних точок, то:

• точка а належить півпрямій РА_Н;

• п ряма А_НА кар­ти­нної площини буде перспективою прямої .

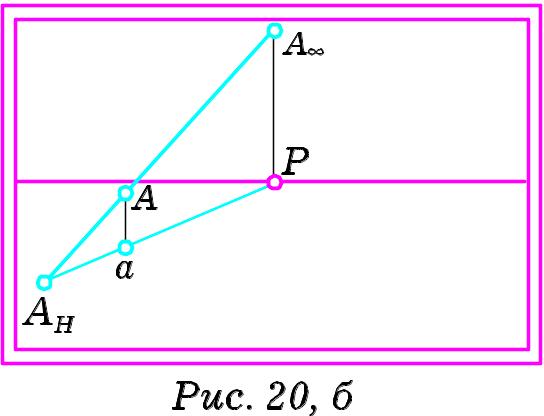
Встановимо де буде розташована гранична точка прямої. Точку знаходимо від перетину променя зору, паралельного до прямої , з картиною. З означення висхідної прямої випливає, що промінь зору лежить в площині головного променя зору. Тому точка лежить на головному вертикалі картини над лінією горизонту. Отже, для побудови перспективи висхідної прямої, досить продовжити пряму до перетину з лінією головного вертикалу. Перспективу прямої зображено на картині (Рис. 20, б).

Н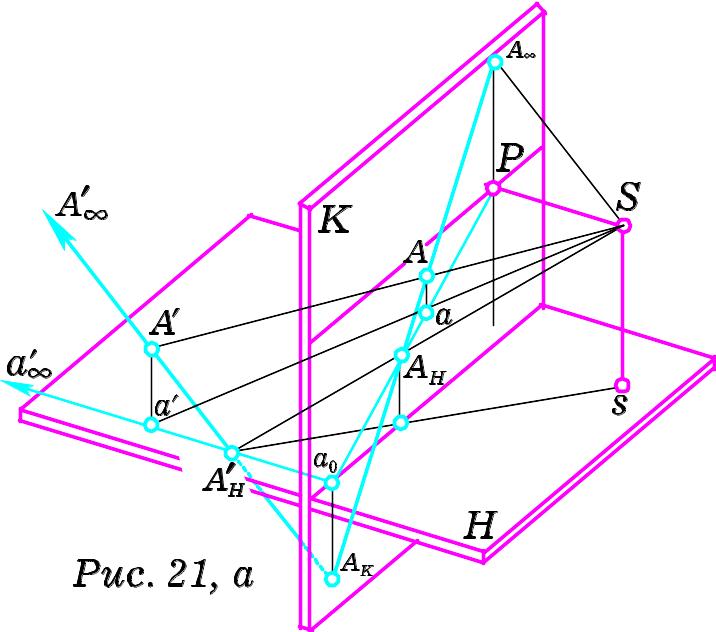 ехай тепер – точ­ка перетину проекції вис­хідної прямої з карти­нною площиною (ос­но­вою картини kk). Картин­ний слід цієї прямої особ­ливого розміщення лежа­тиме під основою кар­ти­ни на пер­пен­дикулярі до kk, про­­ве­де­ному через точ­ку (Рис. 21, а). Якщо А перс­пек­тива точки А´ висхідної прямої, то точки А_K, А та А_∞ лежатимуть на одній пря­мій – перспективі пря­мої , точки , А_K та P лежатимуть на перспективі її проекції.

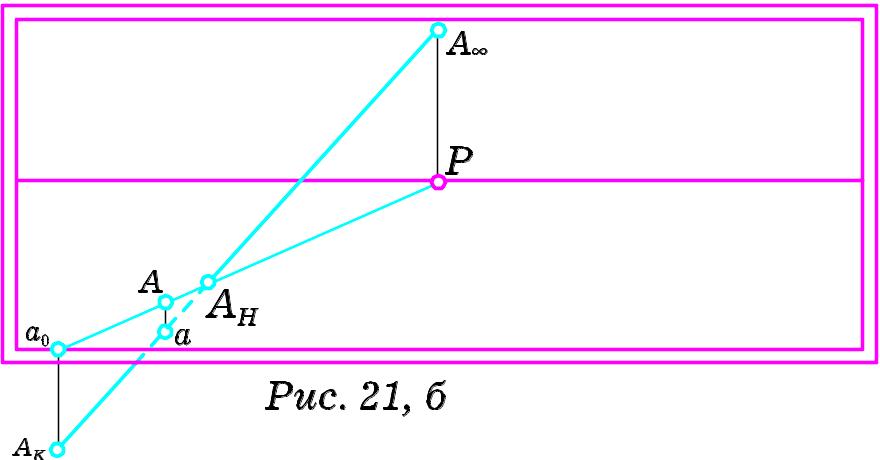
Н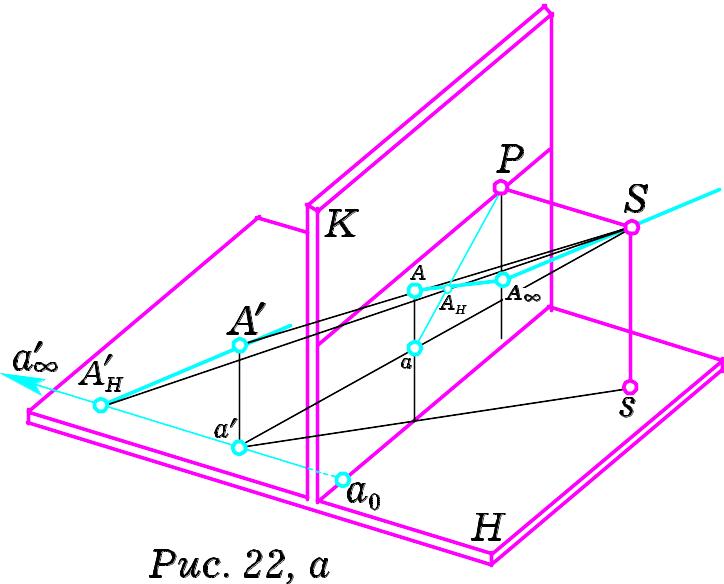 а Рис. 21, б побудовано перспективу висхідної прямої особливого розміщення. Слід запам’ятати, що гранична точка висхідної пря­мої особливого роз­мі­щення розташована на лінії головного вертикалу над горизонтом, а проекція її граничної точки співпадає з головною точкою картини.

На Рис. 22, а задано нисхідну пряму особливо­го розміщення , її про­екцію на предметну пло­щину та пред­мет­ний слід . Нехай А – перспектива точки А´, а – перспектива її проекції. Сполучимо точку а з головною точкою картини. Одержимо перспективу проекції нисхідної прямої на предметну площину.

З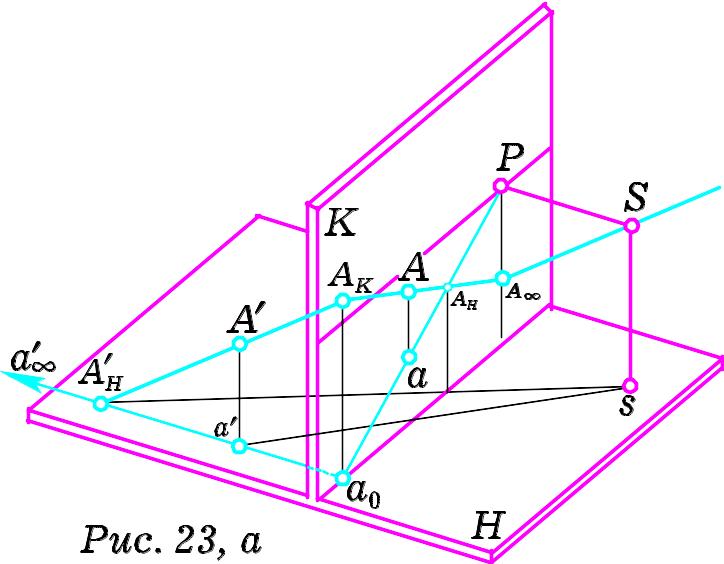 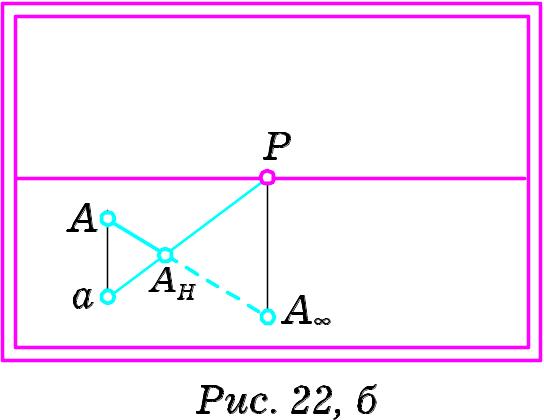найдемо предметний слід прямої . Для побудови зображення нисхідної прямої досить провес­ти пряму до перетину з лінією головного верти­ка­лу. Дійсно, як і висхідна, нисхідна пряма паралельна до пло­щини основного променя зору. Тому промінь зору пара­лельний до прямої перетне картину в точці, яка належить лінії головного вертикалу. Тому гранична точка нис­хідної прямої лежа­ти­ме на головному вертикалі під лінією горизонту.

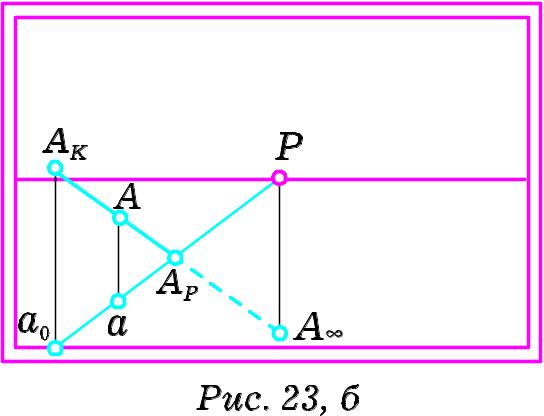
Нехай – точка перетину прямої з основою кар­тини kk (Рис. 23, а). У площині картини через точку проведемо вертикальну пряму. Картинний слід лежатиме на побудо­ваній вертикальній пря­мій. Точки A_K, А, та лежа­тимуть на пер­с­­­пективному зобра­жен­ні прямої . При цьому пряма aP про­й­де через точ­ки та . На Рис.. 23, б побудовано перс­пек­тиву нисхідної прямої особ­ливого роз­мі­щення. Слід запам’ятати, що гра­ни­чна точка нисхідної прямої особливого розміщення розташована на лінії головного вертикалу під горизонтом, а проекція її граничної точки співпадає з головною точкою картини.

\