§3. Перспектива точки

Положення точки відносно проекційного апарата назвемо частковим, якщо вона лежить в предметній або картинній площині. В інших випадках положення точки будемо називати загальним.

Н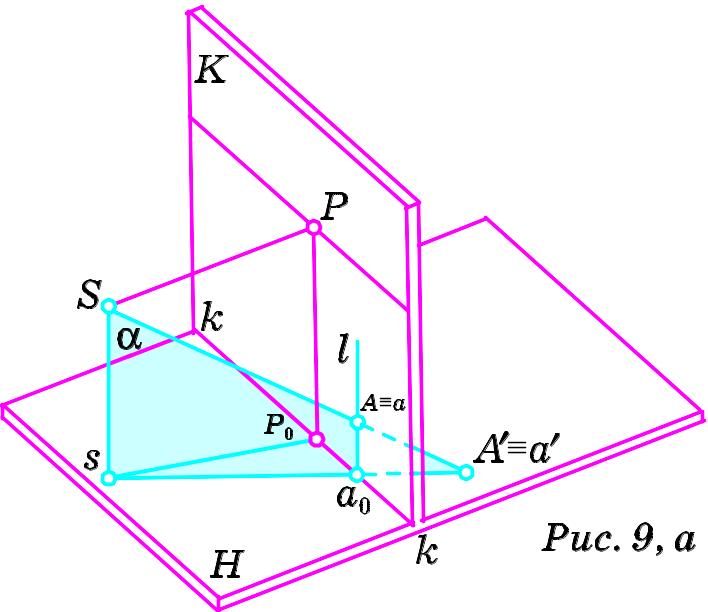 а рис. 9, а задано проекційний апарат і точку A´ в предметній площині. При такому розміщенні точка A´ співпадає зі своєю проекцією a´ на предметну пло­щи­ну (A´≡a´). Побудуємо перспективу точки A´.

Для знаходження точки перетину променя зору SA' з площиною картини, розв’яжемо задачу А. Для цього потрібно:

1. включити пряму SA' в деяку площину α;

2. знайти лінію перетину l площин α та K;

3. встановити точку перетину A прямих l та SA'.

1. За α виберемо площину, утворену прямими Ss та SA'.

2. Точки s та a´ – спільні точки площин α та H. Тому лінією перетину площини α з предметною площиною буде пряма sa´. Прямі sa´ і kk перетинаються в точці a_o, яка є спільною точкою площин α та K. Отже лінія перетину картинної площини з площиною α пройде через точку a_0. Для побудови лінії перетину площин α та K необхідно знайти ще одну їхню спільну точку або встановити напрямок їх лінії перетину. Оскільки кожна з площин α та K перпендикулярна до предметної площини, то лінія їх перетину (пряма l) також перпендикулярна до площини H, а отже до прямої kk, що лежить в предметній площині.

3. Шукану точку A одержуємо від перетину прямих l та SA'.

На рис. 10 подано перспективу точки A´ часткового розміщення. ЇЇ положення на картині визначається відстанню p_oa_o праворуч від лінії головного вертикалу та відстанню a_oa – відстанню від точки A до основи картини. Зауважимо, що відрізок a_oa є перспективою відрізка a_oA´.

З міркувань 1 – 3 випливає така послідовність побудов для одержання перспективи точки, яка лежить в предметній площині:

1) через точку стояння і задану точку предметної площини проводимо пряму;

2) встановлюємо точку перетину побудованої прямої з основою картини;

3) через встановлену точку в площині картини проводимо перпендикуляр до її основи;

4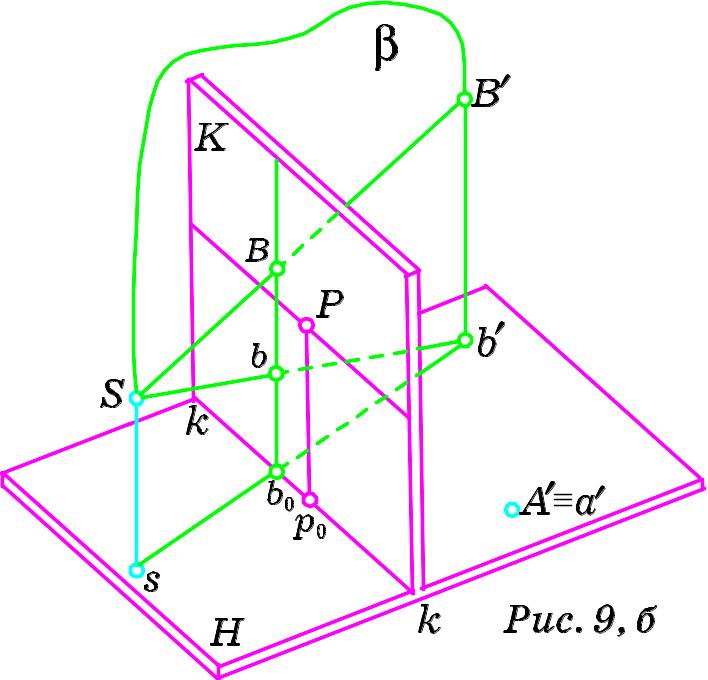 ) шукану точку одержуємо від перетину побудованого на картині перпендикуляра з променем зору, проведеним в задану точку часткового розміщення.

Нехай тепер точка B´ розташована в предметному просторі, b´ – її проекція на пред­метну площину (рис. 9, б). Просторове поло­ження точки B´ визначається положенням її проекції b´ в предметній площині і довжиною відрізка B´b´. Побу­дова перспективи точки загального розміщення зво­диться до побудови перспективи її проекції на пред­метну площину. Доведемо це.

Побудуємо спочатку перспективу точки b´ за схемою, поданою вище:

1) через точку стояння s і задану точку b´ пред­метної площини проводимо пряму sb´;

2) встановлюємо точку перетину b₀ побудованої прямої з основою картини;

3) через встановлену точку b₀ в площині картини проводимо перпендикуляр до її основи;

4) шукану точку b одержуємо від перетину побудованого на картині перпендикуляра з променем зору SB´.

П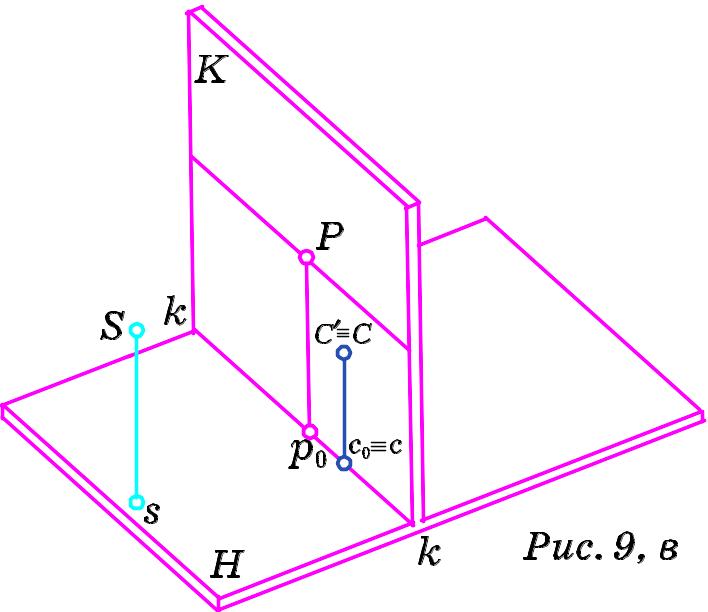 рямі b₀b, sS та B´b´ лежать в площині β, утвореній прямою Ss і променем зору SB´. Лінією перетину площини β з предметною площиною є пряма sb´, яка перетинає площину картини в точці b₀. Пряма b₀b є лінією перетину площин β та K. Тому шукану перс­пективу B точки загального розміщення B´ одержимо від перетину променя зору SB´ з прямою b₀b.

Побудову перспективи точки загального розмі­щен­ня проводимо в такій послідовності:

1. сполучаємо точку стояння з проекцією заданої точки на предметну площину;

2. встановлюємо точку перетину побудованої пря­мої з основою картини;

3. через встановлену точку в площині картини проводимо перпендикуляр до її основи;

4. перспективу шуканої точки одержуємо від перетину побудованого на картині перпендикуляра з променями зору, проведеними в задану точку та її проекцію на предметну площину.

Н а картині (рис. 10) просторове положення точки B визна­чають відстанню p₀b₀ ліворуч від лінії головного вертикалу та пер­пендикуляром bB , проведеним до основи картини, який виз­начає висоту точки над предметною площиною.

Розглянемо ще один випадок часткового розміщення точки. Якщо точка C´ розміщена в площині картини, то вона співпадає зі своїм картинним слідом C (рис. 9, в). При цьому основа c точки співпадає з проекцією c₀ точки C´ на основу kk картини.