
- •Міністерство освіти та науки україни національний технічний університет
- •1Згинання прямолінійних стержнів
- •1.1Класифікація згинання та типи опор
- •1.3 Диференціальні залежності при згинанні
- •2. Напруження при поперечному згинанні.
- •2.1 Нормальні напруження при чистому згинанні.
- •2.2 Дотичні напруження при поперечному згинанні.
- •2.3 Розподіл дотичних напружень для прямокутного перерізу.
- •2.4 Розподіл дотичних напружень для двотаврового перерізу.
- •2.5 Порядок виконання проектувального розрахунку при згинанні.
- •2.6 Потенційна енергія деформації при згинанні.
- •3. Переміщення при прямому згинанні. Розрахунки на жорсТкість при згинанні.
- •3.1 Диференціальне рівняння вигнутої осі.
- •3.2.1 Інтеграл Максвелла-Мора.
- •3.2.2 Геометричний спосіб обчислення інтеграла Максвела-Мора. Спосіб перемножування епюр.
- •34. Загальні вказівки по виконанню розрахунково-проектувальних робіт і вимоги до їхнього оформлення
- •3.1План розвязання
- •3.1.1Послідовність виконання завдання
- •Література
- •3.1.1.1.12.1 Нормальні напруження при чистому згинанні
- •3.1.1.2Навчальне видання
- •61002, Харків, вул. Фрунзе, 21.
3.2.1 Інтеграл Максвелла-Мора.
Розглянемо
балку довжиною
,
навантажену в точці 1 силою
(рис. 3.3). Визначимо переміщення![]() (у точці 2 від сили, прикладеної в точці
1).
(у точці 2 від сили, прикладеної в точці
1).
1.
Перший стан.
У точці 1 прикладемо зосереджену силу
F. Прогин у точці 1 дорівнює
![]() ,
у точці 2 -
.
У перерізах балки виникає згинальний
момент від зовнішнього навантаження
,
у точці 2 -
.
У перерізах балки виникає згинальний
момент від зовнішнього навантаження
![]() .
Сила F прикладається статично і виконує
роботу
.
Сила F прикладається статично і виконує
роботу
![]() на шляху
(див. графік на рис.3.3.1). Визначаємо
потенційну енергію деформації, виражену
через згинальний момент
,
за формулою (3.12):
на шляху
(див. графік на рис.3.3.1). Визначаємо
потенційну енергію деформації, виражену
через згинальний момент
,
за формулою (3.12):
![]() .
Але потенційна енергія деформації
.
Але потенційна енергія деформації
![]() чисельно
дорівнює роботі зовнішніх сил
чисельно
дорівнює роботі зовнішніх сил
![]() ,
тобто:
,
тобто:
![]() .
.
2.
Другий стан.
У точці 2 статично прикладемо одиничну
силу, що, згинаючи балку, виконує роботу
(див. графік на рис.3.3.2) на переміщенні
![]() .
У перерізах балки виникає згинальний
момент
від одиничної сили. Робота одиничної
сили
.
У перерізах балки виникає згинальний
момент
від одиничної сили. Робота одиничної
сили
![]() .
Потенційна енергія деформації
.
Потенційна енергія деформації
![]() .
Як і в попередньому випадку
.
Як і в попередньому випадку
![]() .
.

Рис.3.3.
3.
Третій стан.
У точці 2 статично прикладемо одиничну
силу, що, деформуючи балку, виконує
роботу
![]() на переміщенні
(див. графік на рис. 3.3.3). До деформованої
балки статично у точці 1 прикладемо
зосереджену силу
,
що, деформуючи балку з уже прикладеною
одиничною силою, виконує роботу
(див. графік) на переміщенні
.
Точка 2 одержить ще переміщення
,
а одинична сила виконає роботу
на переміщенні
(див. графік на рис. 3.3.3). До деформованої
балки статично у точці 1 прикладемо
зосереджену силу
,
що, деформуючи балку з уже прикладеною
одиничною силою, виконує роботу
(див. графік) на переміщенні
.
Точка 2 одержить ще переміщення
,
а одинична сила виконає роботу
![]() (див. графік) на переміщенні
.
Від дії сили
й одиничного навантаження в перерізах
балки виникає сумарний згинальний
момент
(див. графік) на переміщенні
.
Від дії сили
й одиничного навантаження в перерізах
балки виникає сумарний згинальний
момент
![]() .
Робота двох сил визначиться як:
.
Робота двох сил визначиться як:
![]() ,
,
а потенційна енергія пружної деформації виразиться через сумарний згинальний момент як:
![]() .
.
Порівнюючи
вирази для![]() ,
після нескладних перетворень одержимо:
,
після нескладних перетворень одержимо:
![]() .
(3.5)
.
(3.5)
Порядок визначення переміщень за допомогою інтеграла Максвелла-Мора.
Прикладаємо зовнішнє навантаження, визначаємо опорні реакції, розбиваємо балку на ділянки, записуємо вирази (функції) згинаючого моменту для кожної ділянки.
У точці, переміщення якої визначаємо, прикладаємо:
Одиничну силу при визначенні прогину (лінійного переміщення);
Одиничний момент при визначенні кутового переміщення.
Визначаємо опорні реакції й у такому ж порядку, як і для зовнішнього навантаження, на кожній ділянці записуємо вирази (функції) згинаючого моменту .
Підставляємо функції (вирази) і в інтеграл Максвелла-Мора та робимо відповідні обчислення.
Результат обчислень позитивний, якщо напрямок одиничного навантаження, що прикладається, збігається з напрямком дійсного переміщення, і негативний, якщо напрямок одиничного навантаження, що прикладається, не збігається з напрямком дійсного переміщення.
Приклад
2. Консольна
балка постійного поперечного перерізу
(ЕIx=const)
довжиною
навантажена на кінці зосередженою силою
(рис.3.4а).
Визначити прогин
![]() та
кут
та
кут
![]() повороту на кінці консолі.
повороту на кінці консолі.
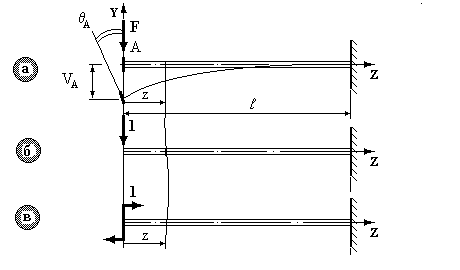
Рис. 3.4.
Запишемо функцію
 (рис.3.4а).
(рис.3.4а).У точці
 прикладаємо одиничну силу (рис.3.4б)
та записуємо функцію
прикладаємо одиничну силу (рис.3.4б)
та записуємо функцію
 .
.Підставляючи й в інтеграл, одержимо:
 (див. приклад
1
на рис. 3.2).
(див. приклад
1
на рис. 3.2).Для визначення кутового переміщення у точці прикладаємо одиничний момент (рис.3.4в) та записуємо функцію
 .
.Підставляючи й в інтеграл, одержимо:
 .
.
Результат
обчислення прогину
позитивний, тому що прикладена одинична
сила збігається з напрямком дійсного
переміщення. Результат обчислення кута
повороту
![]() негативний,
тому що прикладений одиничний момент
по напрямку не збігається з дійсним
напрямком кута повороту перерізу в
точці
.
негативний,
тому що прикладений одиничний момент
по напрямку не збігається з дійсним
напрямком кута повороту перерізу в
точці
.
