2.2 Дотичні напруження при поперечному згинанні.

Дія в перерізі поперечної сили викликає дотичні напруження , що збігаються по напрямку з нею, по ширині перерізу не змінюються та визначаються за формулою Д.И.Журавського:

, (2.10)

де - поперечна сила, що діє в перерізі; - осьовий момент інерції перерізу щодо центральної осі X (нейтральної лінії); - ширина перерізу на тім рівні у від нейтральної лінії, де визначаються дотичні напруження; - абсолютне значення статичного моменту щодо центральної осі X частини перерізу, що лежить вище чи нижче того рівня, де визначаються дотичні напруження. Умова міцності по дотичним напруженням при поперечному згинанні записується у вигляді:

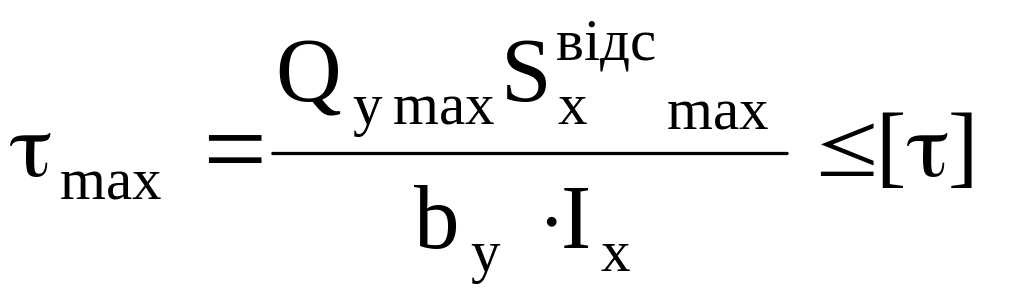(2.11)

Таким чином, при прямому поперечному згинанні маємо умови міцності по нормальним та дотичним  напруженням. Основним вважається умова міцності по нормальним напруженням, а умова (2.11) по дотичним напруженням, як правило, перевіряється. Використання формули Д.И.Журавського розберемо на прикладах.

2.3 Розподіл дотичних напружень для прямокутного перерізу.

В перерізі діють М_х момент і поперечна сила , спрямовані, як показано на рис.2.6. Поперечна сила , ширина перерізу та осьовий момент інерції конкретні постійні величини (рис.2.6). Таким чином, дотичні напруження змінюються за таким же законом, що і статичний момент відсіченої частини площі .

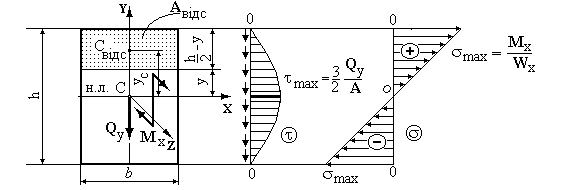
Рис.2.6.

Визначаємо дотичні напруження на рівні y. Площа відсіченої частини перерізу , положення її центра ваги 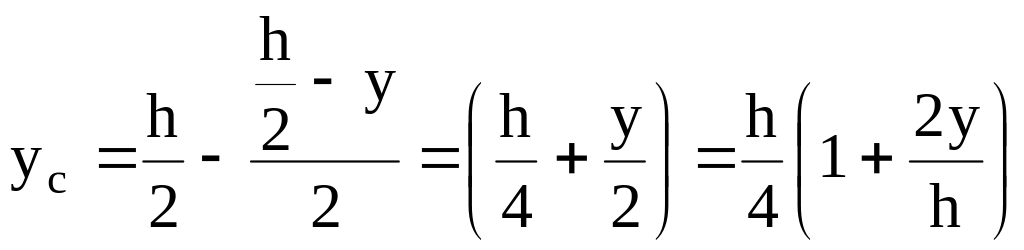. Статичний момент відсіченої частини площі:

Таким чином, дотичні напруження змінюються за законом квадратної параболи. Максимальні дотичні напруження виникають на нейтральній лінії, де нормальні напруження дорівнюють нулю. Для визначення необхідно обчислити статичний момент половини площі перерізу , і максимальні дотичні напруження визначаться як: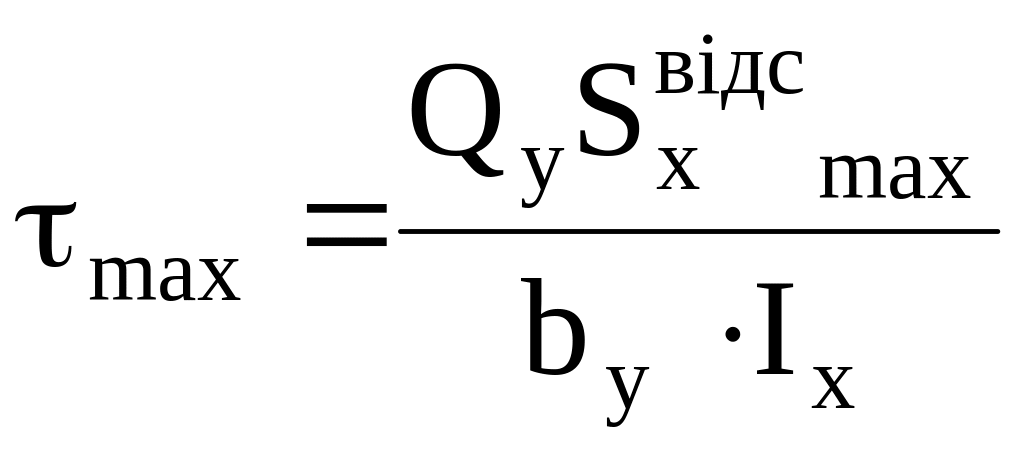 . Для прямокутного перерізу , маємо: .

2.4 Розподіл дотичних напружень для двотаврового перерізу.

. В перерізі діють згинальний М_х момент та поперечна сила , спрямовані, як показано на рис.2.7.

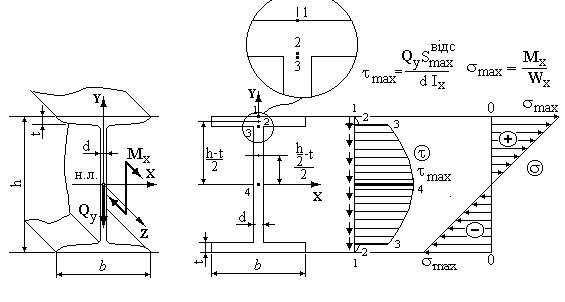
Рис.2.7.

Використовуючи вираз (2.10) для дотичних напружень, визначимо їхні значення в характерних точках.

Точка 1: , тому що (вище рівня 1 відсічена площа відсутня).

Точки 2,3. Ці точки мають однакову координату y, але належать полиці та стінці одночасно , тобто різній ширині b₂=b; b₃=d. Тому в місці переходу полки в стінку виникає скачок дотичних напружень.

Точка 2 (приналежна полиці): ;

Точка 3 (приналежна стінці): ;

Точка 4: .

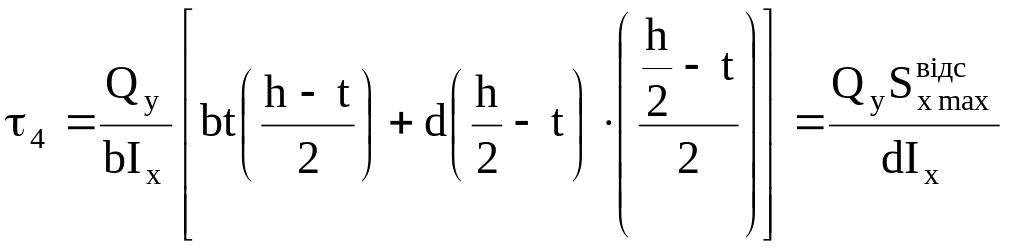- статичний момент щодо центральної осі половини площі перерізу, для стандартних профілів приведений у таблицях сортаменту. Зразковий графік розподілу дотичних напружень приведений на рис 2.7. Дійсний розподіл дотичних напружень трохи відрізняється від отриманого, тому що полиці мають ухили, а перехід від полиці до стінки здійснюється по радіусу кривини.