6.2. Лінійна залежність і незалежність функцій і розв"язків лінійних диференціальних рівнянь

значення3. Дві функції називаються лінійно залежними на відрізку , якщо існують числа , не рівні нулю одночасно ( ), такі, що для будь-якого справджується тотожність

. ( 6 )

Якщо ж тотожність є справедливою тільки при , ці функції називаю-ться лінійно незалежними.

Теорема 2. Дві функції лінійно залежні на відрізку тоді і тільки тоді, якщо їх відношення тотожно дорівнює сталій на цьому відрізку, тобто якщо для будь-якого

. ( 7 )

■1. Нехай функції лінійно залежні на відрізку , так що тотожність (6) є вірною для . Якщо, наприклад, , то з (6) маємо

,

відношення функцій тотожно дорівнює сталій.

3. Нехай тепер

на . Тоді

,

і функції лінійно залежні за означенням лінійної залежності.■

Приклад 2. Функції для лінійно незалежні на всій числовій осі , оскільки їх відношення не є тотожно сталим.

Означення 4. n функцій називаються лінійно залежними на відрізку , якщо існують n чисел , не рівних нулю одночасно ( ) і таких, що для довільного справедлива тотожність

. ( 8 )

Якщо ж тотожність є справедливою тільки у випадку , то функції називаються лінійно незалежними на .

Приклад 3. Функції лінійно незалежні на , бо многочлен відносно x

тотожно дорівнює нулю тільки тоді, якщо всі його коефіцєнти дорівнюють нулю, тобто якщо если .

В теорії і практиці лінійних диференціальних рівнянь важливе значення має наступний визначник.

Означення 5. Визначником Вронського¹, або вронскіаном n функцій називається наступний визначник n-го порядку:

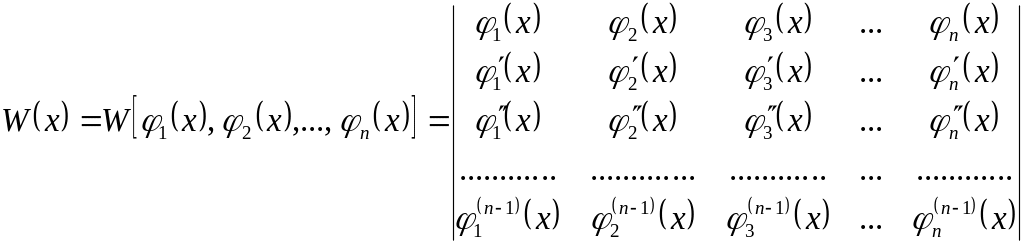( 9 )

Приклад 4. Вронскіан функцій (див. приклад 2) дорівнює

.

Вронскіан є зручним інструментом для встановлення лінійної залежності будь-якої системи функцій і, що є для нас особливо важливим, - лінійної незалежності розв"язків лінійних однорідних диференціальних рівнянь.

Теорема 3. Якщо функції лінійно залежні на відрізку , то їх вронскіан тотожно дорівнює нулю на , .

■Нехай, задля простоти, дві функції лінейно залежні на відрізку . За означенням лінійної залежності існують такі два числа , що і тотожно

на . Продиференціюємо цю тотожність і утворимо таку систему лінійних алгебричних рівнянь відносно :

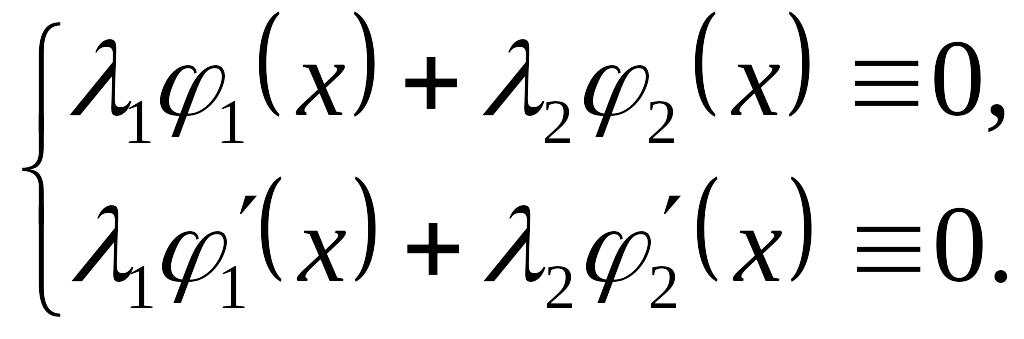
Для будь-якого система має нетривіальний (ненульовий) розв"язок, а тому її головний визначник тотожно дорівнює нулю на відрізку ,

.■

Для випадку тільки двох (але не більше) функцій теорему мо-жна довести ще простіше. Дійсно, відношення цих лінійно залежних функцій тотожно дорівнює сталій на . Нехай, наприклад,

Тоді , і вронскіан функцій дорівнює

.

Теорема 4. Якщо функції

є лінійно незалежними розв"язками лінійного однорідного диференціального рівняння n-го порядку з коефіцієнтами, неперервними на деякому відрізку, то вронскіан цих розв"язків не перетворюється в нуль в жодній точці відрізка.

■Доведення теореми проведемо від супротивного. Для простоти розглянемо випадок двох лінійно незалежних розв"язків лінійного однорідного рівняння (3) другого порядку з неперервними на відрізку коефіці-єнтами . Припустимо, що вронскіан цих розв"язків дорівнює нулю в деякій точці відрізка, тобто , . Виберемо два не рівних одночасно нулю числа так, щоб пара ( ) була розв"язком наступної системи лінійних алгебричних рівнянь:

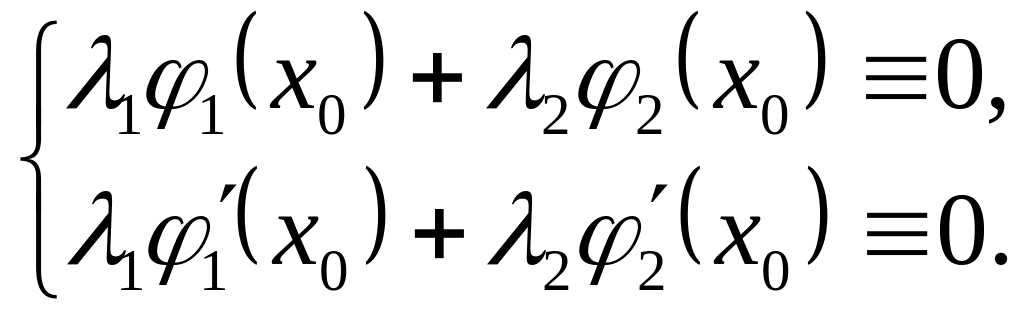( 10 )

Такий вибір можливий, оскільки головним визначником системи (10) є рівне нулю число . Утворимо тепер функцію

.

Вона є розв"язком рівняння (3), що задовольняє нульові початкові умови, а саме умови (10). Отже, на підставі прикладу 1 такий розв"язок тотожно дорівнює нулю, тобто

причому числа не дорівнюють нулю одночасно. Але це значить, що, всупереч умові, функції є лінійно залежними.

Ми дістали протиріччя, яке доводить теорему.■

Приклад 5. Функції (див. приклад 2) є для всіх розв"язками лінійного однорідного диференціального рівняння

,

оскільки для будь-якого x

і аналогічно

.

Ці розв"язки лінійно незалежні, а їх вронскіан (див. приклад 4) не дорівнює нулю в жодній точці.