
- •Диференціальні рівняння
- •5. Диференціальні рівняння першого і другого порядків
- •5.1. Загальні поняття
- •5.2. Інтеґровні типи диференціальних рівнянь першого порядку
- •5.2.1. Рівняння з відокремленими змінними
- •5.2.2. Рівняння з відокремлюваними змінними
- •5.2.3. Однорідні диференціальні рівняння (відносно змінних)
- •5.2.4. Лінійні рівняння
- •5.2.5. Рівняння Бернуллі
- •5.3. Диференціальні рівняння другого порядку, які припускають зниження порядку
- •5.3.1. Рівняння вигляду .
- •5.3.2. Диференціальні рівняння другого порядку, які не містять явно шуканої функції.
- •5.3.3. Диференціальні рівняння другого порядку, які не містять явно незалежної змінної.
- •6. Лінійні диференціальні рівняння другого порядку
- •6.1. Загальні поняття
- •6.2. Лінійна залежність і незалежність функцій і розв"язків лінійних диференціальних рівнянь
- •6.3. Структура загального розв"язку лінійного однорідного диференціального рівняння
- •6.4. Лінійні однорідні диференціальні рівняння з сталими дійсними коефіцієнтами
- •6.4.1. Характеристичне рівняння
- •6.4.2. Корені характеристичного рівняння – дійсні і різні
- •6.4.3. Корені характеристичного рівняння – дійсні рівні
- •6.4.4. Корені характеристичного рівняння – комплексні
- •6.5. Лінійні неоднорідні рівняння
- •6.5.1. Структура загального розв"язку
- •6.5.2. Метод варіації довільних сталих Лаґранжа1
- •6.5.3. Метод невизначених коефіцієнтів
- •6.5.4. Принцип суперпозиції
- •7. Нормальні системи диференціальних рівнянь
- •7.1. Загальні поняття
- •7.2. Метод виключення для інтеґрування нормальної системи диференціальних рівнянь першого порядку
- •8. Поняття про наближені методи інтеґрування диференціальних рівнянь
- •8.1. Метод послідовних наближень
- •8.2. Метод ейлера1
- •5. Диференціальні рівняння першого і другого порядків 312
5.2.3. Однорідні диференціальні рівняння (відносно змінних)
Означення 11. Диференціальне рівняння першого порядку називається однорідним (відносно змінних x, y), якщо його можна подати у вигляді
![]() ,
( 15 )
де
функція в правій частині залежить тільки
від відношення змінних.
,
( 15 )
де
функція в правій частині залежить тільки
від відношення змінних.
Теорема 4. Однорідне диференціальне рівняння (15) зводиться до рівняння з відокремлюваними змінними введенням нової шуканої функції
![]() .
(
16 )
.
(
16 )
■Знаходячи та підставляючи його значення в рівняння, маємо
![]()
![]() .
.
Отримане рівняння є рівнянням з відокремлюваними змінними за умови
![]() .
.
Дійсно, в цьому випадку
![]()
![]() .■
.■
Зауваження 6. Можна довести, що диференціальне рівняння вигляду
![]() ( 17 )
( 17 )
є
однорідним,
якщо для будь-якого
![]() виконується умова
виконується умова
![]() .
.
■Дійсно, покладаючи
![]() ,
можемо подати праву частину рівняння
(17) у вигляді функції від відношення
,
можемо подати праву частину рівняння
(17) у вигляді функції від відношення
![]() :
:
![]() .■
.■
Більш загальне диференціальне рівняння
![]() ( 18 )
( 18 )
є однорідним, якщо для будь-якого існує число k таке, що одночасно
![]() і
і
![]() .
.
Доведіть це твердження самостійно.
Приклад 9. Розв"язати задачу Коші
![]() .
.
Поділимо обидві частини рівняння на x. Отримаємо диференціальне рівняння вигляду (15),
![]()
в якому права частина
![]()
є
функцією від
відношення![]() .
Отже, задане
рівняння є
однорідним.
Діючи згі-дно з теорією,
маємо
.
Отже, задане
рівняння є
однорідним.
Діючи згі-дно з теорією,
маємо
![]()
![]()
Дякуючи довільності сталої C, ми можемо відкинути тут знаки абсолютної величини, звідки
![]() .
.
Початкова умова дає
![]() .
.
Шуканий розв"язок задачі Коші
![]() ,
,
або
![]() .
.
Приклад 10. Знайти загальний розв"язок диференціального рівняння
![]() .
.
Рівняння є однорідним, оскільки для довільного маємо
![]() .
.
Однорідність рівняння можна встановити без залучення . Перепишемо для цього його у вигляді
![]()
та
поділимо чисельник і знаменник дробу
праворуч на
![]()
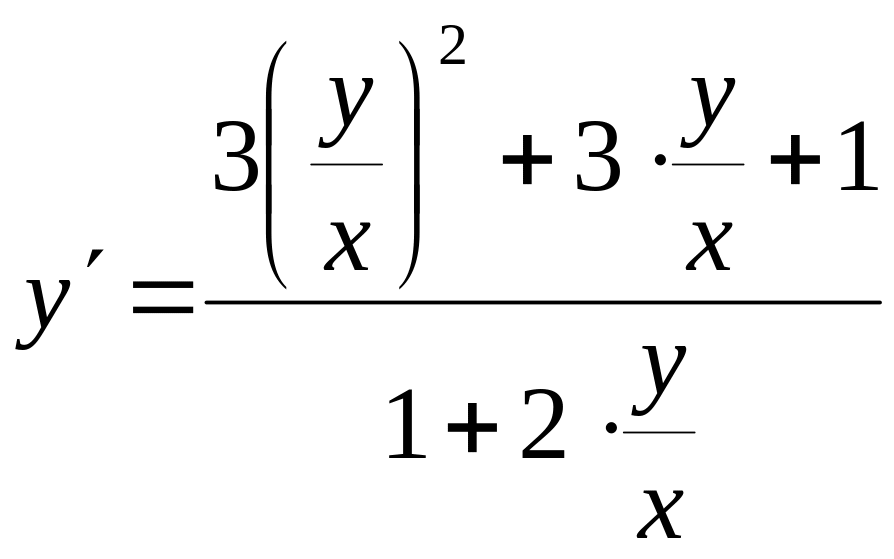 .
.
В отриманому рівнянні права частина є функцією від відношення , що доводить однорідність даного рівняння. На підставі теорії, застосованої до перетвореного рівняння, дістаємо
![]()
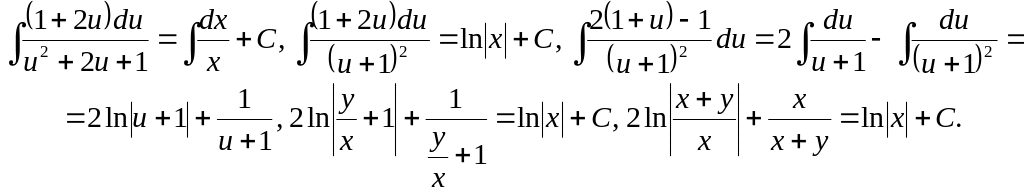
Приклад 11.
Знайти криву, яка
проходить через точку
![]() ,
якщо піддотична в довільній
її точці
дорівнює сумі
координат цієї точки.
,
якщо піддотична в довільній
її точці
дорівнює сумі
координат цієї точки.
З умови випливає, що шукана крива не може перетинати вісь Ox і тому знаходиться вище неї.
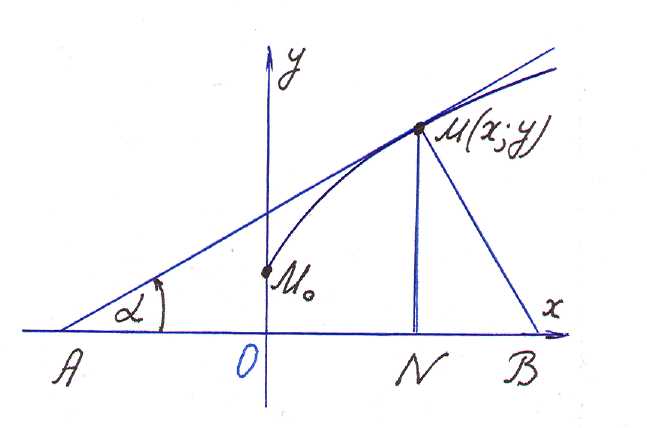 Нехай
Нехай
![]() - рів-няння шуканої кривої,
- рів-няння шуканої кривої,
![]() і
і
![]() - від-повідно відрізки дотичної
і нормалі до кривої в довільній
її точці
,
і
- від-повідно відрізки дотичної
і нормалі до кривої в довільній
її точці
,
і
![]() (див. рис.
2 для випадку
(див. рис.
2 для випадку
![]() ).
Напрямлені відрізки
).
Напрямлені відрізки
![]() і
і
![]() називаються
відповідно піддо-
Рис. 2
тичною та піднормаллю до кривої
в точці
.
називаються
відповідно піддо-
Рис. 2
тичною та піднормаллю до кривої
в точці
.
З прямокутного трикутника![]() (у випадку
(у випадку![]() точка A лежить
ліворуч від точки N,
рис. 2, у випадку
точка A лежить
ліворуч від точки N,
рис. 2, у випадку
![]() - праворуч) маємо
- праворуч) маємо
![]() ;
;
те
ж саме значення для![]() можна отримати, виходячи з рівняння
дотичної до шуканої кривої в точці
.
Дійсно, рівняння дотичної має вигляд
можна отримати, виходячи з рівняння
дотичної до шуканої кривої в точці
.
Дійсно, рівняння дотичної має вигляд
![]()
Покладаючи
тут
![]() ,
матимемо
,
матимемо
![]() .
.
Довжина піддотичної дорівнює
![]() ,
,
і на підставі умови ми дістаємо диференціальне рівняння
![]()
з початковою умовою
![]() .
.
Таким чином, ми повинні розв"язати задачу Коші.
Перший випадок
![]() .
.
Для визначення типу рівняння запишемо його у вигляді
![]()
і поділимо чисельник і знаменник дробу на x,
 .
.
Ми бачимо, що отримане рівняння має вигляд (15), а отже дане рівняння є однорідним. Використовуючи теорію, матимемо
![]()
![]()
![]() .
.
Початкова умова дає
![]() .
.
Шукана крива має наступне рівняння:
![]() ,
,
![]() .
.
Другий випадок
![]() .
.
Інтеґрування рівняння (яке також є однорідним) дає
![]()
![]()
![]()
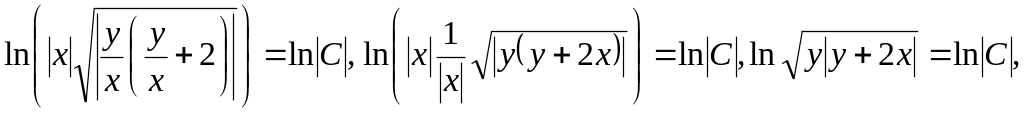
![]()
Початкова умова може
виконуватись тільки
у випадку![]() :
:
![]() ,
,
і отже шукана крива дається рівнянням
![]() .
.
Відповідь. Поставлена задача має два розв"язки:
, .
