146

Застосування диференціального числення. 1. Функції однієї змінної

3. Застовування диференціального числення

3.1. Дослідження функцій однієї змінної

3.1.1. Умови зростання і спадання функці

Теорема 1 (необхідна умова зростання функції). Якщо диференційовна функція однієї змінної зростає на деякому інтервалі, то її похідна на цьому інтервалі є невід"ємною.

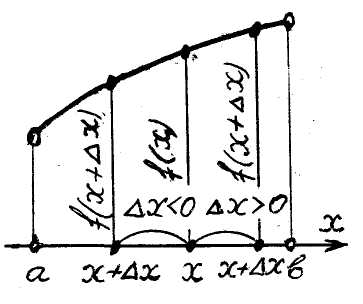■Нехай функція зростає на інтервалі (a, b), x – довільна точка інтервала, а приріст арґументу x настільки малий, що точка лежить на (a, b) (рис. 1). Якщо приріст арґументу додатний, , тобто , то приріст функції в точці x додатний,

,

Fig. 1 а тому . Якщо ж , , то приріст функції в точці x від"ємний,

,

тому . Таким чином, в обох випадках ( і ) відношення приросту функції до відповідного приросту арґументу додатне. На ос-нові теорії границь (див. п. 1.1.3. А, властивість 4) похідна функції в точці x є невід"ємною, тобто

.■

Зауваження. Аналогічно, нерівність на інтервалі (a, b) є необхід-ною умовою спадання функції на (a, b).

Теорема 2 (достатня умова зростання функції). Якщо функція неперервна на деякому відрізку , а на інтервалі (a, b) має додатну похідну, , то функція зростає на .

■Нехай на інтервалі (a, b), а - дві довільні точки відрізка такі, що (рис. 2). За теоремою Лагранжа існує точка , для якої

.

Рис. 2 Оскільки і, згідно з умовою теореми, , маємо

,

тобто функція зростає на відрізку .■

Зауваження. Аналогічно, нерівність на інтервалі (a, b) є достатньою умовою спадання функції на відрізку , якщо вона неперер-вна на цьому відрізку.

Приклад. Довести, що функція, яка неявно задана рівнянням еліпса

,

спадає на відрізку .

■За правилом диференціювання неявної функції маємо

.■

Приклад. Функції, які неявно задано відповідно рівняннями гіперболи і параболи

,

зростають в першому квадранті.

Достатньо ще раз застосувати правило диференціювання неявної функції, згідно з яким відповідно

Завершіть доведення самостійно.

3.1.2. Локальні екстремуми

Означення 1. Точка називається точкою локального максимуму функції , якщо існує деякий окіл цієї точки ( на рис. 3) такий, що для будь-якої точки з проколе- Рис. 3 ного околу виконується нерівність

.

Значення функції в точці , тобто , називається локальним максимумом функії.

Аналогічно означається точка локального мінімуму і локальний мінімум функції (точки на рис. 3 і відповідні значення функції).

Терміни локальний максимум і локальний мінімум об"єднуються спільним терміном локальний екстремум.

Означення 2. Точка з області визначення функції називається критичною точкою функції, якщо її похідна в цій точці дорівнює нулю або не існує.

Зокрема,

Означення 3. Точка називається стаціонарною точкою функції, якщо її похідна в цій точці дорівнює нулю,

Теорема 3 (необхідна умова існування локального екстремуму). Якщо функція має локальний екстремум в точці , то ця точка є критичною точкою функції.

Справедливість теореми випливає з теореми Ферма.

Зауваження. З теореми 3 випливає, що функція може мати локальний екстремум тільки в своїй критичній точці. З іншого боку, критична точка не обо-в"язково є точкою локального екстремуму, тобто необхідна умова існування екстремуму зовсім не є достатньою.

Приклад. Точка є критичною (а саме стаціонарною) для функції

( ), але вона не є точкою локального екстремуму, оскільки при і при .

Теорема 4 (перша достатня умова існування локального максимуму). Якщо функція не- Рис. 4 перервна в своїй критичній точці , в інтервалі , в інтервалі (рис. 4), то функція має локальний максимум в цій точці.

■Доведення випливає з теореми 2 і подальшого зауваження до неї: функція зростає в інтервалі , спадає в інтервалі і, крім того, є неперер-вною в точці . Отже, вона має в цій точці локальний максимум.■

Аналогічно дається достатня умова існування локального мінімуму в критичній точці, якщо нерівності в умові теореми 4 замінити на такі: в інтервалі , в інтервалі . Функція, графік якої зображено на рис. 4, має локальний мінімум в критичній точці b (зауважмо, що похідна функції в цій точці не існує, бо точка є кутовою точкою графіка функції).

Теорема 5 (друга достатня умова існування локального екстремуму функ-ції в її стаціонарній точці). Нехай - стаціонарна точка функції , тобто (див. означення 3), і, крім того, друга похідна функції в цій точці відмінна від нуля, . За цих умов точка є точкою локального максимуму при і точкою локального мінімуму при .

■Нехай, наприклад,

.

З теорії границь випливає (див. п. 1.1.3. А, властивість 4), що для достатньо малого приросту арґументу маємо

.

З останьої нерівності випливає, що при і

при Отже, функція зростає зліва від точки і спадає праворуч від неї, і, таким чином, має локальний максимум в цій точці.■

Зауваження. З теорії границь (п. 1.1.3. А, властивість 3) випливає, що якщо функція є неперервною в точці a і має в ній додатне значення,

,

то вона є додатною в деякому околі точки a.

Виходячи з останнього зауваження, ми можемо дати інше доведення теореми 5, якщо додатково припустимо, що функція в деякому околі точки має похідну другого порядку, неперервну в самій точці. У цьому випадку ми в змозі застосувати для доведення теореми формулу Тейлора.

■ Нехай, наприклад, . На підставі припущення і зробленого зауваження маємо в деякому околі точки . Візьмемо спільну частину околів і і подамо приріст функції в точці фор-мулою Тейлора (див. (24) в п. 2.3.4. В) для ,

.

Тут , а c – деяка точка з околу , причому . Отже, в при-ріст функції є від"ємним, тобто >0 і тому для будь-якої точки , відмінної від . Це значить, що функція має локальний максимум в точці .■

Приклад. Знайти інтервали зростання, спа-дання і локальні екстремуми функції

. Рис. 5 Розв"язання. Функція визначена на множині всіх дійсних чисел. Її похідна дорівнює

,

вона дорівнює нулю в точці і не існує в точці . Ці точки, тобто , , є критичними точками функ-ції. Методом інтервалів знаходимо інтервали, в яких похі-дна функції має сталий знак (коротше – інтервали знако-сталості похідної). Розподіл знаків (див. рис. 5) свідчить про те, що функція зростає на інтервалі і спадає на Рис. 6 інтервалі . Отже, вона має локальний мінімум в точці , рівний

.

Зауваження. Задана функція дорівнює нулю в точках , додатна на об"єднанні , від"ємна на , її границя на дорівнює . Приблизний графік функції показано на рис. 6. Графік проходить через точки

,

для лежить вище, а для - нижче осі . При прямуванні x до він необмежено здіймається вгору.