2. 3. Комплексная проводимость. Параллельное соединение ветвей

Комплексной проводимостью называется отношение комплексного тока к комплексному напряжению данного участка цепи : .

Очевидно, что . Подставляя в эту формулу , получим

, (2. 21)

где - полная проводимость участка цепи : .

Применяя к равенству (2. 21) формулу Эйлера, перепишем его в виде

, (2. 22)

где - активная проводимость;

- реактивная проводимость.

Используя алгебраическую запись комплексного сопротивления (2. 10) , комплексную проводимость можно представить еще и так :

, (2. 23)

или

.

Сравнивая равенства (2. 22) и (2. 23), устанавливаем, что

. (2. 24)

Понятиями и величинами комплексной проводимости удобно пользоваться при параллельном соединении ветвей (рисунок 2. 9) .

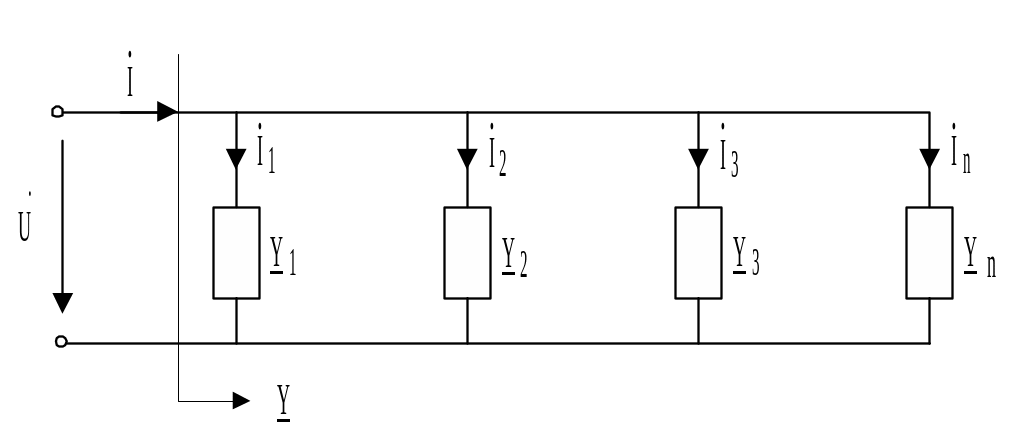
Рисунок 2. 9

Общий ток является суммой токов отдельных ветвей :

.

Величина является общей комплексной проводимостью цепи. Очевидно, что ее можно определить, суммируя активные и реактивные (с учетом знака) составляющие комплексных проводимостей ветвей.

Пример. Определить комплексную проводимость цепи, приведенной на рис. 2. 10. На основе формул (2. 24) находим

.

.

Следует заметить, что рассчитывать общий ток параллельного соединения через его общую проводимость имеет смысл, если это соединение входит как составная часть в более сложную цепь. Если же напряжение на зажимах параллельного соединения задано (идеальный источник напряжения), то токи в отдельных ветвях находятся по закону Ома, а общий ток- по первому закону Кирхгофа в комплексной форме.

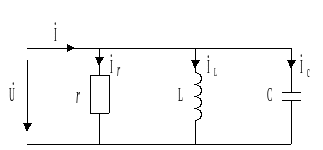
Рисунок 2. 10

Пример. Определить токи в цепи рисунке 2.10, если . Находим комплексные токи в ветвях :

.

Общий комплексный ток найдем как сумму токов :

;

его модуль равен . Для наглядности определение тока показано на векторной диаграмме (рисунок 2. 11).

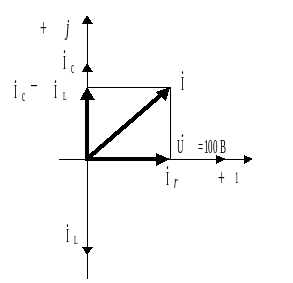
Рисунок 2. 11

Если в параллельном соединении имеется только две ветви, то его эквивалентное сопротивление проще определить не через проводимости, а используя непосредственно сопротивления :

откуда (2. 25)

Пример. Найти полное сопротивление цепи, изображенной на рис. 2. 12,

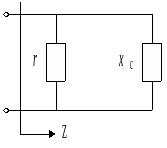
Рисунок 2. 12

если . Подставляя в формулу (2. 25) , находим

или ; .

Заметим, что если бы элементы цепи имели одинаковый характер (оба резисторы или оба конденсаторы), то полное сопротивление равнялось бы 100 Ом.

2. 4. Мощности в цепи гармонического тока

Мгновенная мощность тока в каком - либо участке цепи определяется произведением мгновенных значений напряжения и тока :

При гармонически изменяющихся напряжении и токе

. (2. 26)

Эта мощность изменяется во времени и пользоваться ею для анализа цепи невозможно. Энергетические свойства цепи характеризуются средней мощностью- работой тока, отнесенной к периоду :

. (2. 27)

Среднее за период значение мгновенной мощности называется активной мощностью. Единица измерения активной мощности - Ватт (Вт).

Подставляя формулу (2. 26) в интеграл (2. 27) и учитывая, что

получим

. (2. 28)

Если сдвиг фаз равен нулю, то . В электронике активную мощность принято выражать через амплитудные значения напряжения и тока. Это связано с особенностью работы электронных устройств. Например, амплитудное значение выходного напряжения усилителя не должно превышать допустимой (с точки зрения пробоя транзистора) величины. В электроэнергетике мощность принято рассчитывать через действующие значения напряжения и тока : . Активная мощность таких устройств, как генератора и трансформатора, зависит от напряжения, тока и угла сдвига фаз нагрузки, который может меняться. Поэтому генераторы и трансформаторы удобно характеризовать полной мощностью , равной произведению действующих напряжений и тока.

Эта мощность является максимальной активной мощностью при и допустимых (номинальных) напряжении и токе. Она называется также установочной, или габаритной, так как она определяет габариты генераторов и трансформаторов. Единица измерения полной мощности - вольт- ампер (ВА).

В некоторых случаях находит применение активная мощность, величина которой определяется формулой . Эта мощность положительна при индуктивном характере цепи (Q > 0 при > 0 ) , и отрицательна при емкостном. Единицу мощности в применении к измерению реактивной мощности называют “ВАР” (от сокращения слов “вольт” , “ампер” и “реактивный” ). Реактивной мощностью характеризуют конденсаторы, работающие при больших напряжениях и токах. Например, конденсаторы в сглаживающих фильтрах мощных выпрямителей.

Активная, реактивная и полная мощности связаны соотношениями :

.

Для увеличения коэффициента мощности приемника следует уменьшать реактивную и увеличивать активную мощности. Графически соотношение между мощностями можно представить в виде треугольника мощностей (рисунок 2.13).

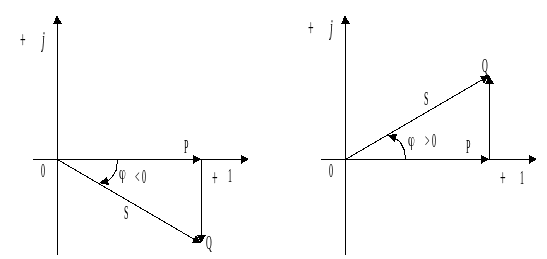
а) б)

Рисунок 2. 13

Мощности электрической цепи могут быть выражены через ее параметры z, r, g, x. Подставляя, например, в формулу (2. 28) вместо его выражение через : , получим или, учитывая, что , . Если вместо подставить , то, с учетом , получим . Аналогично можно выразить полную и реактивную мощности.