Тема 3. Линейные электрические цепи переменного тока

Линейные электрические цепи переменного тока — это линейные электрические цепи, в которых напряжения, токи, ЭДС являются произвольными функциями времени (т.е. сигналами).

3.1 Основные понятия теории линейных электрических цепей переменного тока

Применительно к переменным электрическим сигналам , , введены следующие основные понятия.

Мгновенное значение сигнала — значение сигнала в рассматриваемый момент времени. Обозначается малыми буквами: i, u, e .

Периодический сигнал а(t) — это сигнал, мгновенное значение которого повторяется через равные промежутки времени (см.рис.3.1). Период сигнала Т — это наименьший интервал повторения сигнала. Для периодического сигнала справедливо .

Частота периодического сигнала f — величина, обратная периоду , которая равна количеству периодов в секунду (рис.3.1). Единица измерения частоты — Герц : .

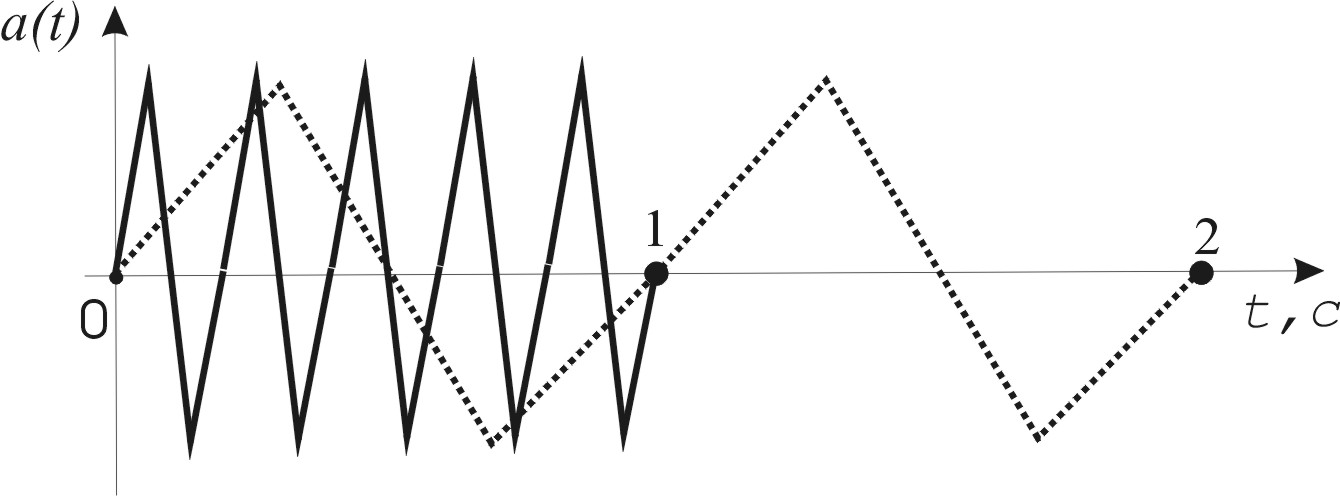
Рисунок 3.1 — Периодические сигналы различных частот:

f =1 Гц (пунктир); f =5 Гц (сплошная линия)

Частотная характеристика (ЧХ) — функциональная зависимость какого-либо параметра цепи от частоты. Например: , .

В электроэнергетике, системах связи, радио и телевидения наиболее часто применяются простые гармонические сигналы, т.е. токи, напряжения, ЭДС, мгновенные значения которых изменяются по синусоидальному закону (рис.3.2), т.е. направление тока или напряжения периодически изменяется (+/-) .

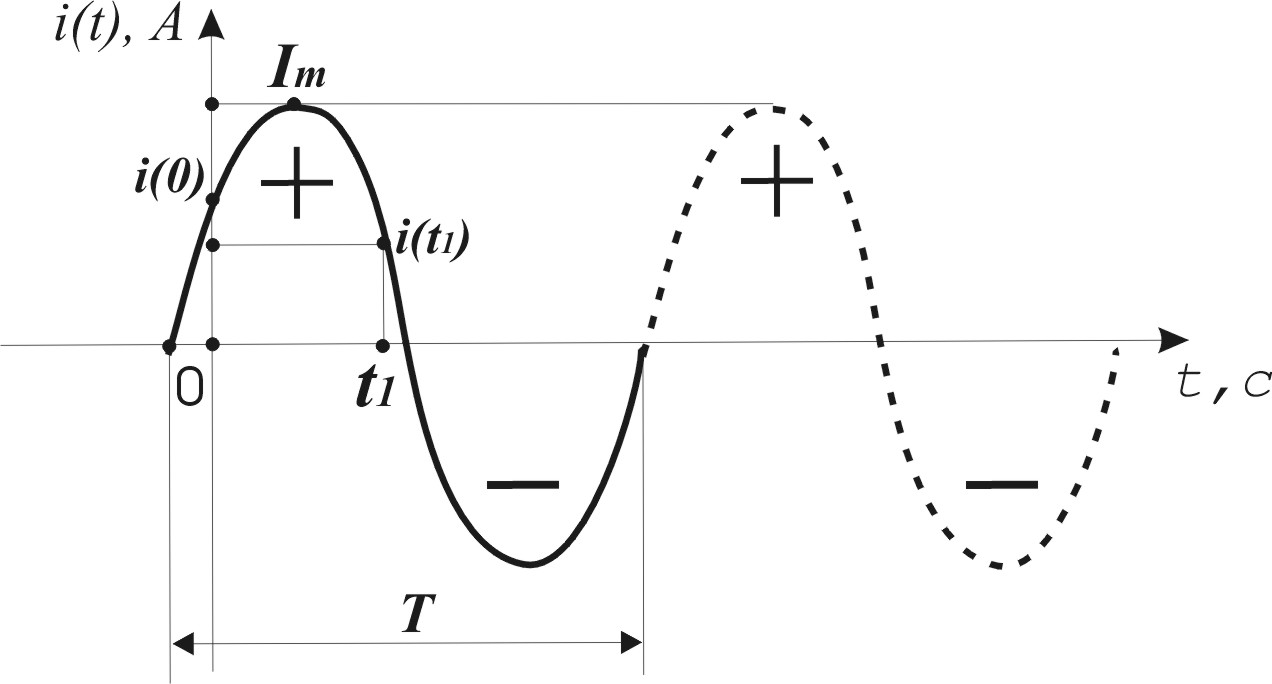
Рисунок 3.2 — Пример гармонического сигнала

Для примера запишем закон изменения синусоидального тока (рис.3.2):

,

где — максимальное значение (амплитуда) тока;

— общая фаза тока (аргумент), которая определяет величину и знак мгновенного значения тока;

— круговая частота (скорость изменения cигнала), . Измеряется круговая частота в радианах в секунду;

— начальная фаза тока (значение фазы тока в момент ).

Таким образом, общая фаза определяет изменение знака сигнала, а начальная фаза определяет значение сигнала при (рис.3.3).

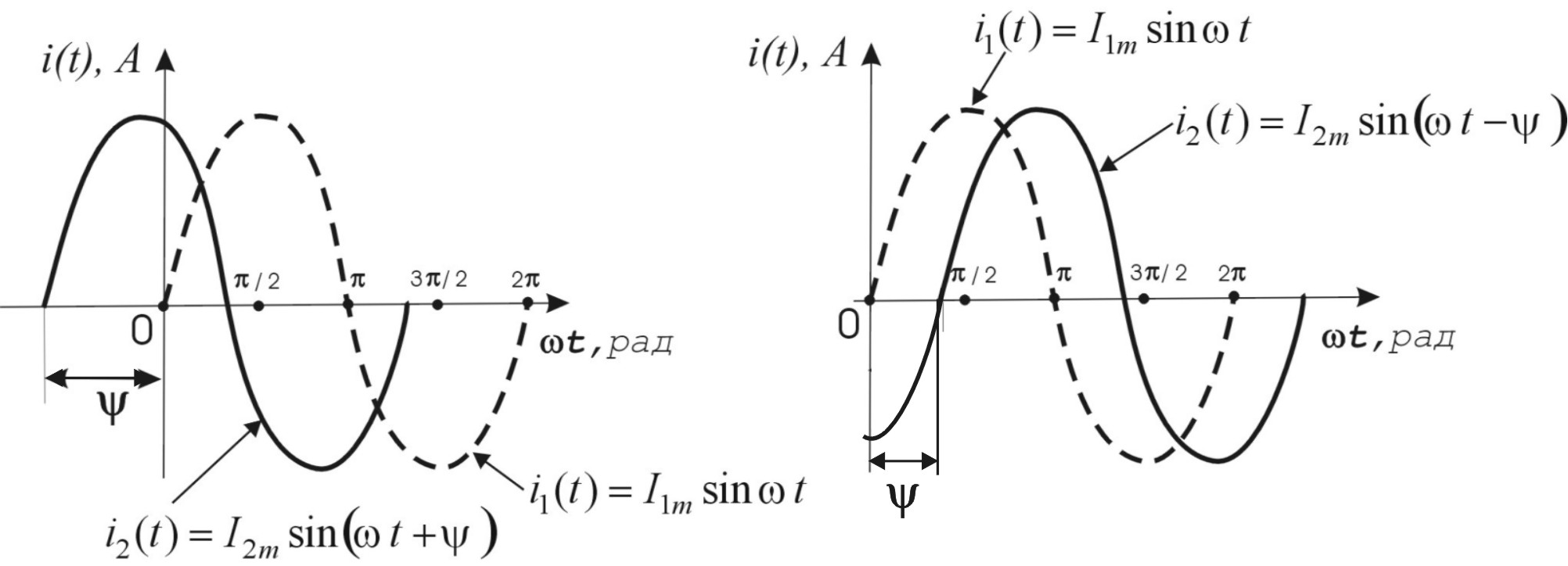
а б

Рисунок 3.3 — Гармонические сигналы с различной начальной фазой

Начальная фаза отсчитывается от точки перехода синусоиды из области отрицательных значений в область положительных (рис.3.3). Положительной начальной фазе соответствует смещение (сдвиг) синусоиды влево от начала координат (рис.3.3а), а отрицательной начальной фазе — сдвиг синусоиды вправо (рис.3.3б). Если два синусоидальных сигнала одинаковой частоты совпадают по фазе (т.е. сдвиг фаз отсутствует), их называют синфазными, если между ними существует сдвиг фаз , они находятся в противофазе.

Действующее значение синусоидального электрического сигнала — это среднеквадратичное значение сигнала за период. Действующее значение является энергетической характеристикой сигнала. Обозначается большими буквами I, E, U : , , .

Если сравнить тепловой эффект (т.е. количество тепла, выделяемого на резисторе) от постоянного и переменного тока за время , то окажется, что возникший тепловой эффект равен в том случае, когда значение постоянного тока равно действующему значению переменного тока.

Связь между действующим и максимальным значением синусоидального тока можно установить следующим образом:

; .

Аналогично , .