Символический метод расчета

Строгий аналитический расчет трехфазных цепей производится сим­волическим методом, т. е. в комплексной форме.

1. Выразим в комплексной форме фазные напряжения:

B ;

= 220 В ;

= 220 B.

2. Выразим сопротивления фаз в комплексной форме:

R_A + jX_LA – jX_CA = 11 + j34 – j53 = (11 – j19) Ом ;

R_B + jX_LB = (11 + j19) Ом ;

– jx_cc = (– 22) Ом

Переведем комплексные сопротивления фаз из алгебраической фор­мы в показательную.

11 – j19 = = 22 Ом ,

где Z_A = 22 Ом - полное сопротивление фазы А ;

- угол сдвига фаз между током и напряжением в фазе А.

Аналогично определяем:

11 + j19 = 22 Ом,

где Z_B = 22 Ом ; ;

– J22 = 22 Ом ,

где Z_С = 22 Ом , 90

3. Находим комплексы фазных токов:

220

= ----- = ---------- = 10 А ,

22

модуль I_А = 10 А, аргумент = 60 ,

220

= ----- = ------------ = 10 А ,

22

модуль I_В = 10 А, аргумент = – 180 ,

220

= ----- = ------------ = 10 А ,

22

модуль I_C = 10 А, аргумент = 210 .

Находим алгебраическую форму записи комплексов фазных токов:

= 10 = 10cos60 + j10sin60 = (5 + j8.66) А ;

= 10 = 10cos(– 180 ) + j10sin(– 180 ) = – 10 А ;

= 10 = 10cos210 + j10sin210 = (– 8.66 – j5) А .

4. Вычисляем ток в нейтральном проводе:

= + + = 5 + j8.66 – 10 – 8.66 - j5 = –13.66 + j3.66 = 14.14 A.

Модуль I_N = 14.14 А, аргумент = 165 .

5. Вычисляем мощности фаз и всей цепи:

= · = 220 · 10 = 2200 =

= 2200 · cos(– 60 ) + j2200 · sin(– 60 ) = (1100 – j1905) B·A ,

где S_А = 2200 В·А; P_A = 1100 Вт; Q_A = – 1905 вар;

= · = 220 ·10 =

= 2200 = 2200 · cos60 + j2200 · sin60 = (1100 + j1905) B·A,

где S_B = 2200 B·А; Р_B = 1100 Bт; Q_B = 1905 вар;

= · = 220 ·10 =

= 2200 = 2200 · cos(– 90 ) + j2200 · sin((– 90 ) = (– j2200) B·A,

где S_C = 2200 B·А; Р_C = 0 Bт; Q_C = – 2200 вар;

тогда

= + + = 1100 – j1905 + 1100 + j1905 –j2200 = 2200 – j2200 = 3111 B·A,

где S = 3111 B·A; P = 2200 Bт, Q = – 2200 вар.

2.5.2. Методика расчета трехфазных электрических цепей переменного тока при соединении треугольником

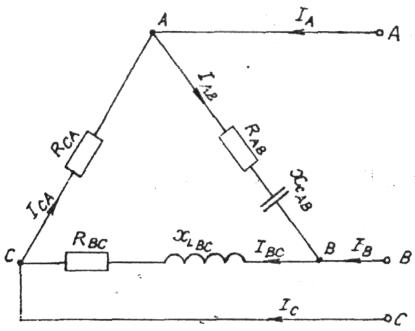
В цепи, изображенной на схеме (рис. 2.40), потребители соединены тре­угольником. Известно линейное напряжение U_Л = 380 В и сопротивления фаз

R_AB = 19 Ом, X_CAB = 11 Ом, R_BC = 12 Ом, X_LBC = 16 Ом, R_CA = 22 Ом.

Определить фазные, линейные токи, мощности активные, реактив­ные, полные мощности каждой фазы и всей цепи. Построить векторную диаграмму цепи.

Дано: U_Л = 380 В,

R_AB = 19 Ом,

X_CAB = 11 Ом,

R_BC = 12 Ом,

X_LBC =16 Ом,

R_CA = 22 Ом.

Определить: I_А, I_B, I_C,

I_AB, I_BC,. I_CA,

P, Q, S

Рис. 2.40

При соединении трехфазной цепи треугольником расчет будем вести символическим методом.

1. Модули фазных напряжений при соединении треугольником рав­ны линейным напряжениям

U_Л = U_Ф = 380 В, то есть U_AB = U_BC = U_CA = 380 В.

Комплексы данных напряжений запишем из условия, что вектор совмещен с действительной осью комплексной плоскости,

= U_л = 380 B;

= U_л = 380 B;

= U_л = 380 B;

2. Вычислим комплексы фазных сопротивлений:

R_AB – jX_CAB = 19 – j11 = 22 Ом, где Z_AB = 22 Ом, = – 30 ;

R_BC + jX_LBC = 12 + j16 = 20 Ом, где Z_BC = 20 Ом, = 53 ;

R_CA = 22 Ом, где Z_CA = 22 Ом, = 0 ;

3. Определяем фазные токи:

380

= ------ = ---------- = 17.27 = (14.96 + j8.64) A, модуль I_AB = 17.27 A, = 30 ;

22

380

= ------ = ------------ = 19 = (–18.86 – j2.32) A, модуль I_BC = 19 A, = –173 ;

20

380

= ------ = ----------- = 17.27 = (–8.64 + j14.96) A, модуль I_CA = 17.27 A, = 120 ;

22

4. Находим линейные токи из уравнений, записанных по первому за­кону Кирхгофа для узлов В, А, С (рис. 2.40).

= – = 14.96 + j8.64 + 8.64 – j14.96 = 23.6 – j6.32 = 24.43 A,

модуль I_А = 24.43 А, аргумент = –15 ;

= – = –18.86 – j2.32 – 14.96 – j8.64 = –33.82 – j10.96 = 35.55 A,

модуль I_B = 35.55 А, аргумент = –198 ;

= – = –8.64 + j14.96 + 18.86 + j2.32 = 10.22 + j17.28 = 20.1 A,

модуль I_C = 20.1 А, аргумент = 59.4 ;

5. Вычисляем мощности каждой фазы и всей цепи:

= ∙ = 380 ∙ 17.27 = 6563 = (5684 – j3282) B∙A,

где S_AB = 6563 B∙A, P_AB = 5684 Вт, Q_AB = –3282 вар;

= ∙ = 380 ∙ 19 = 7220 = (4345 + j5766) B∙A,

где S_BC = 7200 B∙A, P_BC = 4345 Вт, Q_BC = 5766 вар;

= ∙ = 380 ∙ 17.27 = 6563 = 6563 B∙A,

где S_CA = P_CA = 6563 B∙A, Q_CA = 0 вар;

= + + = 5684 – j3282 + 4345 + j5766 + 6563 = 16592 + j2484 = 16777 B∙A,

где S = 16777 B∙A, P = 16592 Вт, Q = 2484 вар;

6. Строим в масштабе векторную диаграмму напряжений и токов.

Векторы фазных токов , , строятся под углами , , к действительной оси. К концам векторов , , при­страиваются отрицательные фазные токи согласно уравнениям:

= – ; = – ; = –

Замыкающие векторные треугольники векторов , , представляют в выбранном масштабе линейные токи. Выбираем масштаб: M_I = 4 А/см.

I_AB 17.27 I_BC 19 I_CA 17.27

= ---- = ------- = 4.3 см; = ---- = ----- = 4.75 см; = ---- = ------- = 4.3 см;

M_I 4 M_I 4 M_I 4

Рис. 2.41