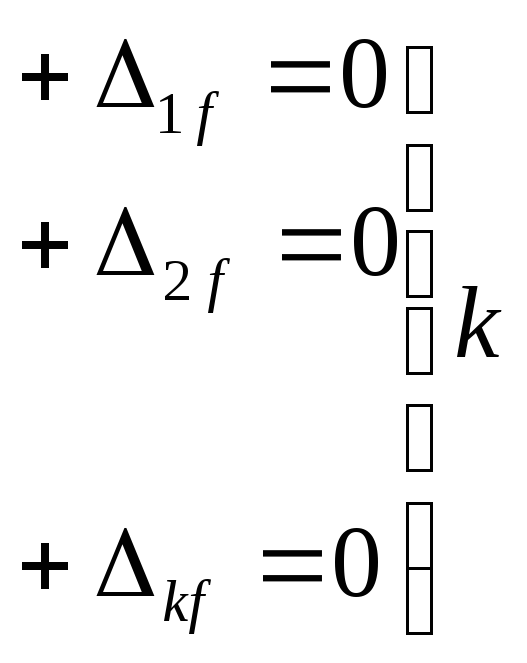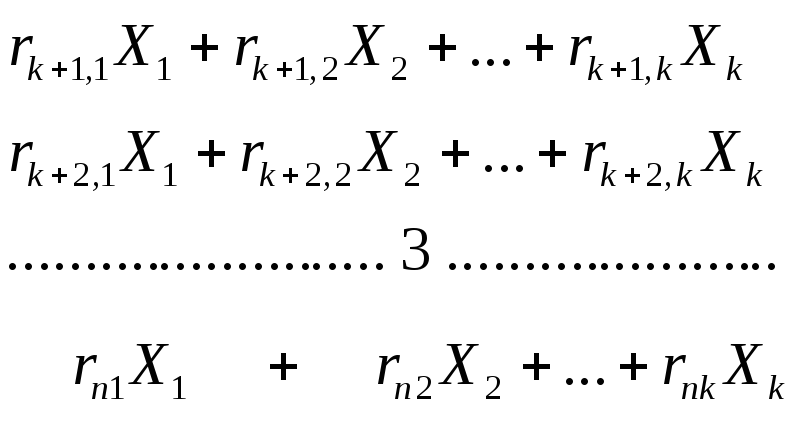Глава 7. Расчет статически неопределимых рам смешанным методом.

7.1. Основные положения метода

В методе, предложенном в 1927 г. профессором А.А.Гвоздевым, объединены идеи методов сил и перемещений. Для получения основной системы смешанного метода устраняются связи, как в методе сил, в той части сооружения, где число неизвестных при расчёте этим методом мало, и вводятся дополнительные связи, метода перемещений, в той части сооружения, где мало число неизвестных при расчёте методом перемещений. За неизвестные принимаются усилия в отброшенных связях или перемещения по направлению введённых связей . Для многих систем число неизвестных смешанного метода получается меньше, чем число неизвестных при решении задачи просто методом сил или просто методом перемещений.

На рис.7.1 приведены примеры таких систем. Здесь же показаны основные системы для расчёта их методами сил, перемещений и смешанным.

Уравнения смешанного метода можно разбить на две группы. При общем числе неизвестных , из которых - неизвестные метода сил, в первую группу из уравнений входят уравнения, выражающие условия равенства нулю перемещений по направлению отброшенных связей, а во вторую из уравнений входят уравнения, выражающие условие равенства нулю реакций во введенных связях.

			(7.1)

В уравнениях (7.1) различают четыре типа коэффициентов (обозначены цифрами 1, 2 ,3 и 4):

1. Коэффициенты, представляющие собой перемещения по направлению отброшенных связей, вызванные усилиями (последние полагают равными единице), т.е. это обычные коэффициенты уравнений метода сил, которые вычисляются "умножением" единичных эпюр.

2. Коэффициенты, представляющие собой перемещения по направлению отброшенных связей, вызванные единичными смещениями

введённых связей. Они находятся или из чисто геометрических соображений, или на основании теоремы о взаимности реакций и перемещений (см. п. 7.4) после определения коэффициентов 3-го типа, т.к. последнее обычно бывает проще.

2. Коэффициенты, представляющие собой реакции во введённых связях от действия единичных усилий .Эти коэффициенты находят статическим методом подобно тому, как определяются свободные члены уравнений метода перемещений.

3. Коэффициенты, представляющие собой реакции во введённых связях, вызванные единичными смещениями этих связей, т.е. это обычные коэффициенты метода перемещений, вычисляемые статическим методом.

Матрица коэффициентов смешанного метода - несимметричная, т.к. связь между симметрично расположенными относительно главной диагонали коэффициентами 2-го и 3-го типов определяется теоремой о взаимности реакций и перемещений .

Свободные члены уравнений первой группы - - определяются так же, как свободные члены в уравнениях метода сил, и имеют одинаковый с ними смысл.

Свободные члены уравнений второй группы - - имеют одинаковый смысл со свободными членами уравнений метода перемещений и вычисляются аналогичным образом.

После решения системы уравнений (7.1) вычисление окончательных значений моментов производится на основании принципа независимости действия сил:

(7.2)

Поперечные и продольные силы определяются так же, как в методах сил и перемещений.

7.2 Пример 1. Построить эпюры внутренних усилий для рамы, изображённой на рис. 7,2, а.

Решение.

1. Данная рама четыре раза статически неопределима. Основная система для расчёта её методом сил показана на рис. 7.2, б. Число неизвестных при расчёте её методом перемещений равно трём, а основная система приведена на рис.7.2, в.

При рассмотрении этих основных систем видно, что в верхнем контуре рамы содержится одно неизвестное метода сил - и два неизвестных метода перемещений -и . Нижний контур содержит три неизвестных метода сил - и одно неизвестное метода перемещений .

Рис. 7.2

Этот анализ определяет выбор основной системы смешанного метода (рис.7. 2, г): в верхнем контуре в качестве неизвестного принято неизвестное метода сил , а в нижнем контуре - неизвестное метода перемещений - .

2. Система канонических уравнений смешанного метода в этом случае содержит только два уравнения:

(7.3)

Первое уравнение обусловливает равенство нулю перемещения по направлению отброшенной связи, а второе - отсутствие реакции во введённой связи.

3. На рис. 7.2, д-ж изображены построенные единичные и грузовые эпюры изгибающих моментов.

4. Определение коэффициентов и свободных членов.

- обычный коэффициент уравнений метода сил.

Его определение сводится к "умножению" эпюры на саму себя. Для такого "умножения" использованы приём Верещагина и формула Симпсона:

- обычный коэффициент уравнений метода перемещений.

Для его определения статическим методом вырезается узел, в который была введена заделка (рис.7.2, е). В местах разрезов прикладываются узловые моменты, значения которых приведены на эпюре . Из условия равенства нулю суммы всех моментов находят реактивный момент :

Аналогичным образом находят значение . Схема вырезанного узла с приложенными к нему моментами показана на рис. 7.2, д.

.

Коэффициент представляет собой перемещение точки (рис.7.2, з) по направлению неизвестного , вызванное единичным перемещением, в данном случае угловым, введенной связи (заделки) в узел . Значение можно найти двумя путями. Первый, наиболее простой, основан на применении теоремы о взаимности реакций и перемещений:

Такое большое значение не является ошибочным: объяснение этому дано в п. 7.4.

Второй путь - кинематический (рис. 7.2, з)

при

Знак "минус" присваивается т.к. направления и противоположны.

находится "умножением" эпюры на эпюру :

(рис. 7. 2, ж) определяется статическим способом аналогично тому, как ранее определялись и :

5. После подстановки найденных значений коэффициентов и свободных членов в систему 7.3 имеем:

(7.4)

Результат решений (7.4): .

6. Окончательная эпюра моментов (рис. 7.2, к) строится с применением формулы (7.2) для случая, когда , . Проверка - равновесие узла .

7. Эпюры и приведены на рис. 7.2, л, м.

8. Проверкой является равновесие рамы.