11.4 Расчет плоской рамы на устойчивость

Пример 2. Схема рамы представлена на рис. 11.3, а, даны ее размеры , отношения жесткостей элементов , нагрузка однопараметрическая, коэффициенты пропорциональности нагрузки .

1. Определяем степень кинематической неопределимости . Выбираем основную систему (ОС) и неизвестные (рис. 11. 3, б).

2. Находим продольные усилия в стержнях рамы и строим эпюры изгибающих моментов от единичных перемещений в основной системе (рис. 11.3, в, г).

Изгибные жесткости всех элементов выражаем через жесткость одного из них, например . Это можно сделать по формуле .

Параметры , учитывающие продольные силы и жесткости элементов также выражаются через один из них, например , по формуле

.

Для заданной рамы (рис. 11.3) ;

3. Произведем оценку параметра устойчивости .

Оценка сверху. Для этого определим параметр устойчивости рамы, полученной из заданной путем постановки дополнительной связи. Это можно сделать путем постановки связи, ликвидирующей горизонтальное перемещение ригеля (рис.11.4). Тогда система имеет одну степень свободы – одну неизвестную по методу перемещений. Для нее система канонических уравнений метода перемещений вырождается в уравнение . Условием его ненулевого решения является .

Рассмотрев равновесие узла 1, получаем или .

Согласно таблице функций устойчивости приближенное значение параметра устойчивости .

Оценка снизу. Определим параметр устойчивости рамы, полученной из заданной путем удаления одной из связей. Для этого в левом верхнем узле рамы поставим шарнир (рис. 11.5). Из условия равновесия рамы получим выражение для единичной реакции :

или .

Приближенное значение параметра устойчивости, полученное подбором, . Таким образом, параметр устойчивости заключается в пределах .

Вернемся к решению задачи для заданной рамы.

Статическим методом из условий равновесия узлов или рамы вычисляем коэффициенты канонических уравнений (рис. 11.3, в, г)

;

;

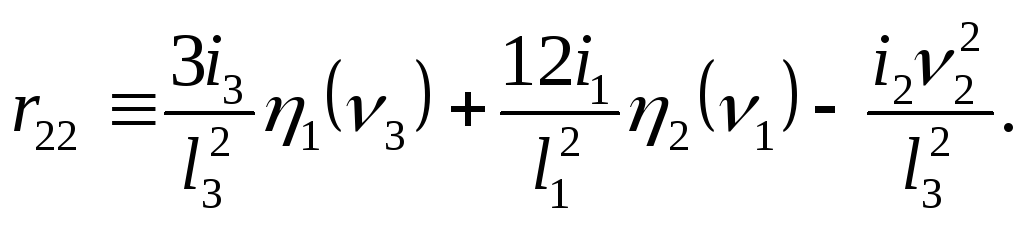
Приравниваем определитель коэффициентов канонических уравнений нулю: .

В раскрытом виде после сокращений имеем уравнение устойчивости

(11.6)

Представим это уравнение следующим образом:

где ;

Уравнение решаем подбором, сведя подсчеты в таблицу 11.3.

Таблица 11.3

		А=0,5+2(1)						f()=AB–C=0
1	2	3	4	5	6	7	8	9
2 3 2,1 2,06	0,859 0,656 0,8437 0,8495	1,359 1,156 1,3437 1,3495	0,598 0,089 0,5565 0,572	0,420 -0,319 0,3588 0,3823	3,20 -3,182 2,6763 2,875	0,931 0,839 0,926 0,9266	3,903 3,170 3,8587 3,8633	0,446 -6,85 -0,2626 0,0144

Корень уточним графически (см. рис. 11.6, б) или аналитически.

Из диапазона величин, полученных при оценке, задаемся несколькими значениями, аргумента (например, ), вычисляем значения функции , т.е. левой части уравнения (11.6).

Для уточнения значения корня вычислим функцию при (см. табл. 11.3). Вычисления нужно производить с большой точностью, а значения функций из таблиц определять путем линейной интерполяции между близкими значениями аргумента. При необходимости получения более точных значений , , , , , их следует вычислять, пользуясь аналитическими выражениями, приведенными в табл. 11.1.

Получаем .

Таким образом, наименьший корень уравнения лежит в пределах , где

1-е приближение

.

Вычисляем значение функции при полученном в первом приближении значении корня (см. последний столбец табл. 11.3): .

Теперь установлено, что наименьший корень лежит в пределах , где

2-е приближение

.

Полученное значения корня можно принять как определенное с точностью до трех значащих цифр.

Соответствующее значение параметра нагрузки:

.

Критические значения сил: , т.е. ; ; .

Рис. 11.7

Для данной задачи физически возможна локальная потеря устойчивости средней стойки при , т.е. одна из форм потери устойчивости основной системы и заданной совпадают. Поэтому нужно вычислить отдельно критическую силу средней стойки. Для нее, как для стержня с двумя шарнирными опорами, эйлеровская крити­ческая сила

.

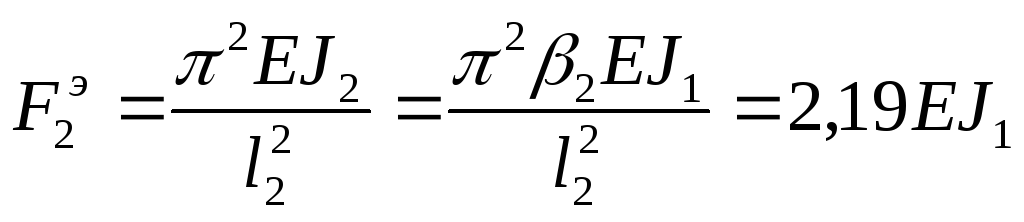Она значительно превышает найденное ранее значение . Таким образом, окончательно критическое состояние всей рамы в целом определяется найденным выше значением параметра , т.е. локальная потеря устойчивости не опасна.

Коэффициент приведенной длины первого стержня определим по формуле

а других стержней -

В данном примере имеем:

.

Вычислим отношение перемещений (форму потери устойчивости):

отсюда

.

Соответствующая форма потери устойчивости показана на рис. 11.7

11.5. Пример 3. (сокращенный: производится лишь оценка параметра устойчивости). Схема рамы приведена на рис. 11.8, а. Размеры: коэффициенты пропорциональности нагрузки коэффициенты пропорциональности изгибных жесткостей стоек и ригеля:

Для данной схемы имеем:

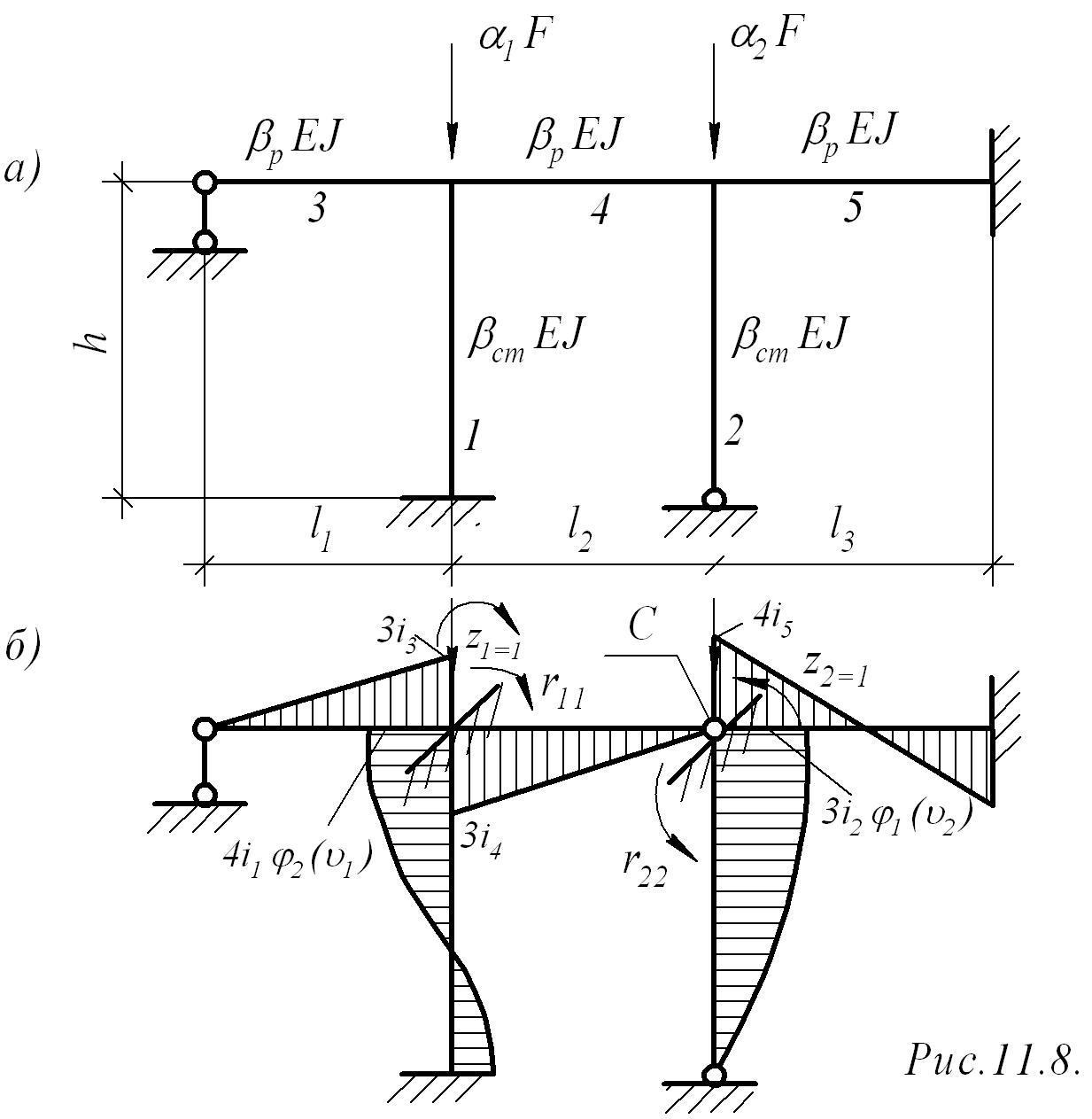
Постановкой шарнира С (рис. 11.8, б) разбиваем раму на две части, для которых параметр устойчивости определяем в отдельности. Для этого в соответствии с методом перемещений в жестких узлах вводим заделки и определяем единичные реакции:

для левой части рамы

отсюда

для правой части рамы

а отсюда

.

Таким образом, критический параметр устойчивости заданной рамы лежит в пределах

.

Значение параметра критической нагрузки для заданной рамы, полученное из решения полного уравнения устойчивости (т.е. для два раза кинематически неопределимой системы) .