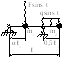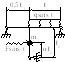12.2.6 Подбор двутаврового поперечного сечения и определение численных значений частот собственных колебаний

По эпюре находится максимальный изгибающий момент. В данном случае .

Определяем требуемый момент сопротивления сечения

.

Выбираем по ГОСТ8239-89 двутавр №30, , , модуль упругости для стали .

Определение численных значений частот и , найденных в п.1 в долях от ;

I.12.3 Задания для расчетно - проектировочных работ на тему «Расчет стержневых систем с двумя степенями свободы на колебания»

Схему принять по рис. 12.11, табл. 12.11.

Порядок выполнения

1. Определить частоты собственных колебаний как функции от .

2. Найти собственные векторы перемещений и изобразить соответствующие им главные формы колебаний.

3. Произвести проверку ортогональности главных форм колебаний.

4. Определить амплитудные значения сил инерции при вынужденных колебаниях.

5. Построить статическую, динамическую и суммарную эпюры моментов. Определить коэффициенты динамики.

6. Подобрать двутавровое сечение и найти численные значения частот собственных колебаний.

II. 12. Расчет статически неопределимых рам с одной степенью свободы, на колебания.

Схему принять по рис. 12.12, 12.13, данные взять из табл. 12.2.

Порядок выполнения

1. Раскрыть статическую неопределимость двух рам, выбрав рациональный метод

2. Определить собственную круговую частоту свободных колебаний

3. Определить перемещение от статически приложенной силы

4. Определить коэффициент динамики

5. Определить динамическую амплитуду колебаний

Пример. Заданная рама рис. 12.6 является системой с одной степенью свободы, поскольку масса может смещаться только вертикально (пренебрегаем продольными деформациями).

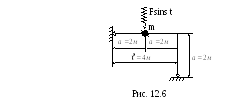
1. Построим эпюру изгибающих моментов 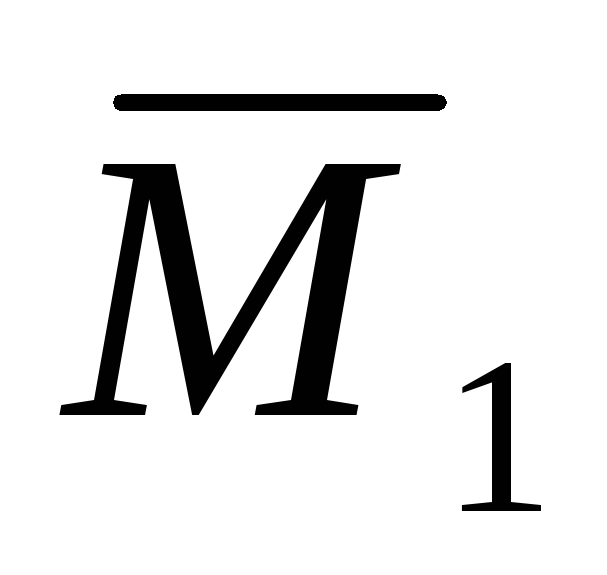от силы , приложенной в центре массы по направлению ее возможного смещения.

2. Определим степень статической и кинематической неопределимости рамы.

, .

Раскроем статическую неопределимость двумя методами.

1. Сначала рассмотрим расчет рамы методом сил. Для этого выбираем основную систему, рис. 12.7, отбросив горизонтальную связь. Загружаем ее усилиями , затем 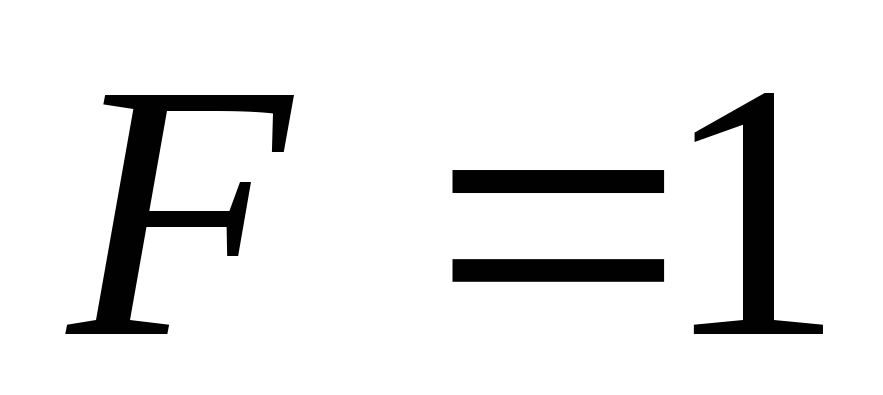. Строим соответствующие эпюры в основной системе (рис. 12.7, б, в). Записываем каноническое уравнение метода сил: , т.к. , то . Находим: .

Тогда неизвестная:

Окончательную эпюру изгибающих моментов построим по формуле (рис. 12.8, б):

2. Построим эпюру изгибающих моментов , используя метод перемещений. Выбираем основную систему (рис. 12. 9, а) метода перемещений, введя жесткую угловую связь. Строим эпюры от единичного поворота (рис. 12.9, б), и грузовую от (рис. 12.9, в).

Запишем погонные жесткости:

(при ) ; (при ).

Каноническое уравнение имеет вид:

, при , .

Выделив узлы из эпюр и (рис. 12.9 б и в) находим:

и , тогда

Окончательную эпюру построим по формуле: (рис. 12.10, а, б).

Эпюры совпали (смотри метод сил).

Построив эпюру от единичной силы двумя методами переходим ко второму этапу - расчету рамы на колебания.

2. Определим круговую частоту свободных колебаний

где, ,

При решении задачи методом перемещений эпюру приходится строить дополнительно. Воспользуемся эпюрами, построенными при расчете рамы по методу сил (перемножаем эпюры и , используя формулу Мора-Верещагина для треугольников или формулу трапеций), для вычисления .

3. Перемещение от статически приложенной силы 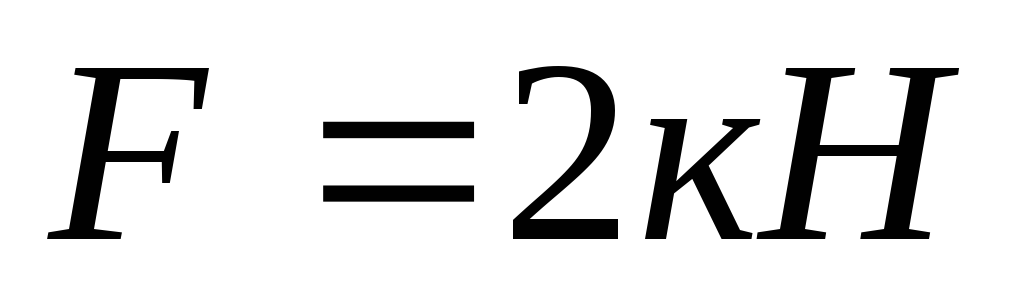будет:

4. Динамический коэффициент при заданном значении найдем по формуле:

5. Динамическая амплитуда колебаний, определяется:

Таблица 12.1 (к рис. 12.11)

Строка
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30	5 5 6 6 7 7 8 8 3 4 5 4 3 3 5 6 5 4 4 5 6 7 5 7 2 3 4 5 2 3	5 7 7 5 6 6 5 4 5 3 3 4 5 4 5 6 5 6 3 4 5 7 4 2 4 5 3 4 2 4	0,4 0,3 0,3 0,25 0,25 0,4 0,3 0,4 0,2 0,4 0,2 0,4 0,4 0,2 0,3 0,4 0,2 0,25 0,35 0,4 0,3 0,2 0,4 0,3 0,5 0,45 0,4 0,35 0,3 0,25	400 500 400 900 800 700 600 500 460 480 500 520 550 580 600 660 630 660 680 700 720 740 760 780 980 990 970 960 940 920	700 500 500 500 400 400 400 300 720 700 680 650 620 600 400 380 350 450 500 530 550 400 440 480 890 860 840 820 810 790	3 0 5 0 4 4 3 0 2 0 3 0 4 0 5 5 0 4 0 3 0 2 0 5 0 6 0 7 0 8	0 0,5 0 0,4 0 0 0 0,3 0 0,6 0 0,7 0 0,8 0 0 0,9 0 1 0 1,2 0 1,1 0 1,3 0 1,4 0 1 0	0,80 0,86 0,90 0,80 0,85 0,90 0,80 0,88 0,80 0,82 0,84 0,86 0,90 0,92 0,94 0,95 0,94 0,93 0,92 0,91 0,90 0,88 0,86 0,80 0,81 0,82 0,83 0,84 0,85 0,85

Рис. 12.11

Таблица 12.2 (к рис. 12.12 и 12.13)

Строка
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30	1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 3,0 1,1 1,3 1,5 1,7 1,9 2,1 2,3 2,5 2,7 2,9 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 4,0	0,50 0,49 0,48 0,47 0,46 0,45 0,44 0,43 0,42 0,41 0,20 0,21 0,22 0,23 0,24 0,25 0,26 0,27 0,28 0,29 0,30 0,31 0,32 0,33 0,34 0,35 0,36 0,37 0,38 0,39	1800 1750 1700 1650 1600 1550 1500 1450 1400 1350 1200 1150 1100 1050 1000 950 900 850 800 750 700 650 600 550 500 450 400 350 300 250	3,9 3,8 3,7 3,6 3,5 3,4 3,3 3,2 3,1 3,0 2,9 2,8 2,7 2,6 2,5 2,4 2,3 2,2 2,1 2,0 1,9 1,8 1,7 1,6 1,5 1,4 1,3 1,2 1,1 1,0	0,95 0,94 0,93 0,92 0,91 0,90 0,89 0,88 0,87 0,86 0,96 0,95 0,94 0,93 0,92 0,91 0,90 0,89 0,88 0,87 0,86 0,85 0,86 0,87 0,88 0,89 0,90 0,91 0,92 0,93	10 10,1 10,2 10,3 10,4 10,5 10,6 10,7 10,8 10,9 11,0 11,1 11,2 11,3 11,4 11,5 11,6 11,7 11,8 1,9 12,0 12,1 12,2 12,3 12,4 12,5 12,6 12,7 12,8 12,9

Примечания: 1) В таблице момент инерции уменьшен в 1000 раз,

2) длину элемента рамы принять а или 2а в зависимости от схемы,

3)  – доля расстояния а до центра массы.

Рис. 12.12

Рис. 12.13

17