Глава 12. Расчет стержневых систем на колебания

I.12.1 Колебания системы с конечным числом степеней свободы

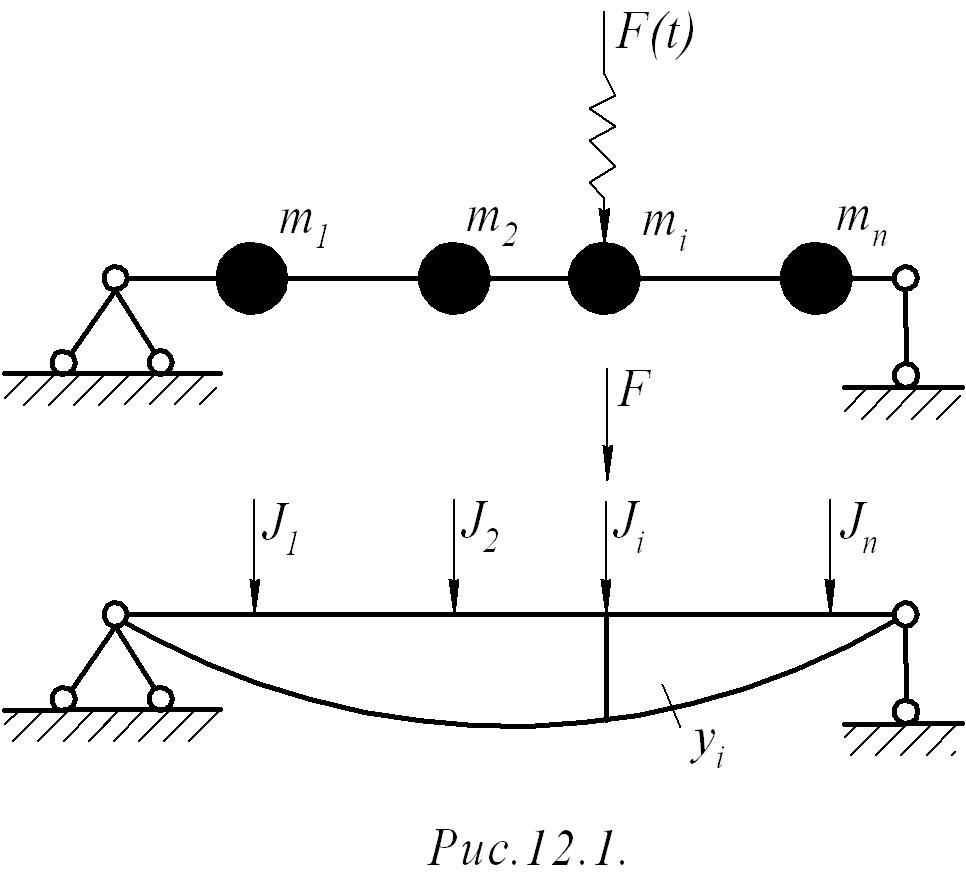
В качестве системы с конечным числом степеней свободы рассмотрим невесомую балку с сосредоточенными массами (рис.12.1).

Перемещение любой - й массы при действии на балку нагрузки , являющейся функцией от времени, можно представить в следующем виде:

, (12.1)

где - сила инерции - й массы;

- перемещение - й массы от единичной силы, приложенной к - й массе;

- перемещение - й массы от внешней нагрузки.

Составляя уравнения, аналогичные (12.1) для каждой массы, получим систему дифференциальных уравнений, общее решение которой указывает на сложный, апериодический характер движения масс.

Особый интерес представляют такие частные решения указанной системы уравнений, которым соответствуют синхронные равно-частотные колебания всех масс. Такой случай возможен при определенных начальных условиях, если внешняя нагрузка отсутствует, т.е. система совершает свободные колебания. Эти свободные колебания называются собственными или главными. Система с конечным числом степеней свободы в этом случае подобна системе с одной степенью свободы, так как все ее точки колеблются с одинаковой частотой и их перемещения следуют гармоническому закону:

(12.2)

где - амплитуда колебаний - й массы;

- частота свободных колебаний;

- начальная фаза колебаний.

Возникающие при этом силы инерции связаны с перемещениями масс и частотой следующей зависимостью:

(12.3)

Подстановка , как это следует из (12.3), в (12.1) приводит к системе однородных уравнений при

(12.4)

где .

Условием ненулевого решения системы (12.4) является характеристическое (вековое) уравнение

(12.5)

Из (12.5) находятся собственные числа , частоты , а из (12.4) собственные векторы, характеризующие главные (собственные) формы колебаний. Частоты , расположенные в порядке возрастания, образуют спектр частот. Главные формы колебаний ортогональны друг другу. Последнее означает, что работа внешних сил, в данном случае сил инерции, или внутренних усилий, ими вызванных, любой - й главной формы колебаний на перемещениях (деформациях), вызванных другой - й главной формой, равна нулю.

Проверка ортогональности - й и - й главных форм колебаний проводится по формуле

, (12.6)

где - координаты собственного вектора, соответствующие - й и - й формам колебаний.

Колебания всех масс системы могут происходить с одинаковой частотой и при установившихся вынужденных колебаниях от действия нагрузки, меняющейся по гармоническому закону, например,

. (12.7)

где - частота вынужденных колебаний.

Перемещения всех масс следуют этому же закону:

. (12.8)

Силы инерции определяются по формуле

(12.9)

Подстановка (12.9) в (12.1) приводит к следующей системе уравнений:

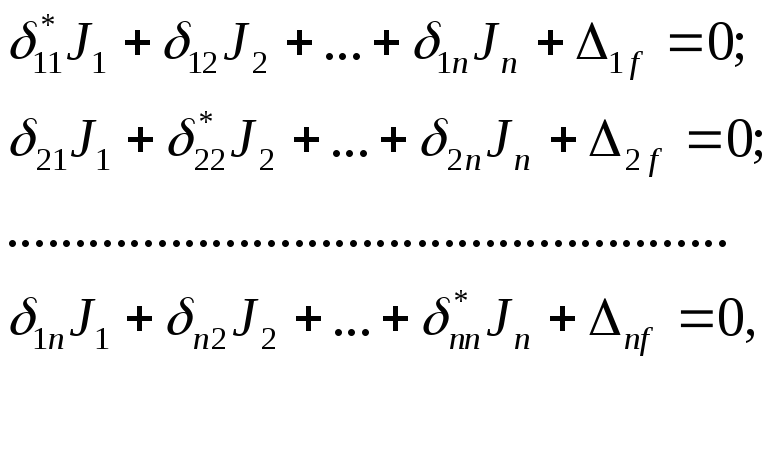(12.10)

где

. (12.11)

Уравнения (12.10) служат для определения сил инерции при вынужденных колебаниях. Как правило, представляют наибольшей интерес амплитудные значения этих сил, в этом случае в (12.10) представляют собой перемещение - й массы от амплитудного значения возмущающей силы.

После определения сил инерции могут быть найдены динамические усилия, в частности моменты , возникающие в системе,

(12.12)

Зависимости (12.10) и (12.12) по форме аналогичны соответствующим зависимостям при расчете статически неопределимых систем методом сил. Это позволяет назвать такой способ изложения и решения дина­мической задачи также методом сил.

Суммарные моменты складываются из статических , вызванных действием веса масс, и динамических

. (12.13)

Динамические усилия резко возрастают при совпадении частоты вынужденных колебаний с одной из собственных частот спектра. Ес­ли не учитывать силы сопротивления, то наступающее при этом явление резонанса характеризуется неограниченным ростом сил инерции, а значит и усилий. Силы сопротивления оказывают наибольшее влия­ние на динамические усилия из-за снижения инерционных сил именно в зоне резонанса. Уже на незначительном удалении от этой зоны их влияние ослабевает. Силы сопротивления в то же время не сильно влияют на значения частот собственных колебаний. Эти обсто­ятельства позволяют использовать расчеты без учета сил сопротив­ления при наличии таковых как при определении спектра собствен­ных частот свободных колебаний, так и при вычислении динамичес­ких усилий в достаточно широком диапазоне частот вынужденных ко­лебаний.