Глава 1. Кинематический анализ шарнирно - дисковых

и шарнирно - стержневых систем.

1. Основные понятия

Любое сооружение должно обладать геометрической неизменяемостью и неподвижностью закрепления, для того чтобы воспринимать и сопротивляться действию произвольной нагрузки, т.е. находиться в равновесии.

Геометрически неизменяемой называется такая система, которая не изменяет свою форму без деформации составляющих ее элементов.

Изменяемая система меняет свою форму, получая произвольные перемещения без изменении размеров элементов конструкций. В строительной механике ведут расчет не реального сооружения, а так называемых расчетных схем. Расчетной схемой называют идеализированную, упрощенную схему сооружения, в которой отражены только основные его свойства.

В качестве расчетных схем применяют лишь геометрически неизменяемые системы. Целью кинематического анализа является выяснение, обладает ли данная система геометрической неизменяемостью, т.е. может ли быть она использована как расчетная схема.

1.2 Степень свободы. Связи.

Степенью свободы системы называется число независимых геометрических параметров, определяющих положение тела в плоскости или в пространстве в любой момент времени.

Точка в плоскости обладает двумя степенями свободы (рис. 1.1, а), в пространстве - тремя. Тело в плоскости обладает тремя степенями свободы (рис. 1.2, б), в пространстве - шестью.

Простым шарниром называется шарнир, соединяющий два стержня (рис. 1.2, а). Если шарнир соединяет более двух стержней (дисков), то он рассматривается как кратный. При соединении «к» дисков кратность шарнира равна «к-1» (рис. 1.2, б).

Шарнир эквивалентен двум связям, опорный стержень - одной связи.

3. Формулы кинематического анализа

Степень свободы плоской кинематической цепи, составленной из дисков, определяется по следующей формуле:

где - степень свободы;

- число дисков (диск - любая плоская неизменяемая система);

- число простых (ординарных) шарниров;

- число опорных стержней.

Выражение (1.1) условие геометрической неизменяеимости и статической определимости.

Степень изменяемости системы (при ) подсчитывается по формуле

Степень свободы шарнирно - стержневой системы (фермы) определяется по формуле

где - число узлов;

- число стержней;

- число опорных стержней;

Если система не имеет опорных стержней, то степень изменяемости

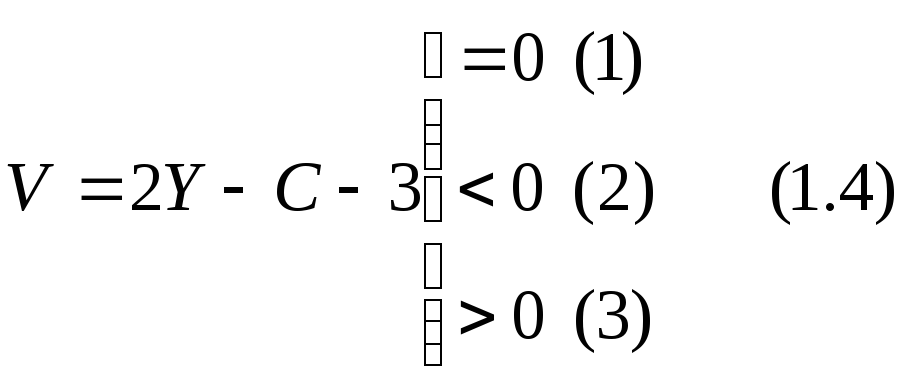
В выражениях (1.1 – 1.4)

1) Системы могут быть неизменяемыми, статически определимыми

2) Системы могут быть неизменяемыми, статически неопределимыми

3) Системы изменяемые

Условия геометрической неизменяемости ( или ) для любой системы являются необходимыми, но недостаточными для утверждения, что данная система действительно является геометрически неизменяемой. Даже в случае или , при наличии в системе лишних связей, они могут быть поставлены так, что в некоторой части система может оказаться изменяемой, а в другой части иметь избыточные связи.

Пример 1.

На рис. 1.3, а представлена многопролетная балка

Исследование структуры: левая часть балки (1-2-3) имеет лишний стержень, правая часть (3-4-5) обладает подвижностью - система изменяема.

Пример 2.

На рис. 1.3, б представлена многопролетная балка

Исследование структуры показывает, что шарниры и опорные стержни расставлены правильно, система геометрически неизменяема.

Шарнирно - стержневые системы, удовлетворяющие условиям (1.3) и (1.4), могут оказаться мгновенно изменяемыми.