3.1.6 Определение расчетных напряжений от постоянной и временной нагрузок

Расчетные усилия, по которым вычисляют напряжения при проверке прочности элементов конструкции, определяются суммированием усилий от постоянной нагрузки (собственного веса) и временной нагрузки (для железнодорожного моста - нагрузка от веса подвижного состава). Каждая из этих нагрузок умножается на свой коэффициент надежности , а временная нагрузка - еще и на динамический коэффициент . Значения коэффициентов надежности дня мостовых конструкций принимаются по соответствующим Нормам. Динамический коэффициент для железобетонных арок равен

где f , l- стрела и пролет арки.

Нормативные эквивалентные нагрузки от подвижного состава ( - класс нагрузки) принимаются по СНиП (в 2.2.4 приведены таблицы эквивалентных нагрузок при ). А также основные правила загружения линий влияния подвижной нагрузкой.

Вычислим напряжения в сечении арки, показанной на рис. 3.10, а, от подвижного состава СК14 и собственного веса, который примем в виде равномерно распределенной нагрузки . Участки (положительный и отрицательный) линий влияния нижнего и верхнего ядровых моментов обозначим номерами I, II, III, IY (рис. 3.10, г, д). Видно, что . Размеры и найдем из уравнений, выражающих условия обращения в нуль ординаты линии влияния момента на среднем участке:

Длины участков линий влияния:

Площади участков:

На рис. 3.10 г, д для каждого участка показаны эквивалентные нагрузки . Их интенсивность подсчитывается в зависимости от и по таблицам эквивалентных нагрузок с учетом интерполяции по и :

Предположим, что рассматривается арочный мост, имеющий в поперечном сечении две арки высотой и шириной каждая. Тогда момент сопротивления относительно горизонтальной оси симметрии равен для одной арки . Коэффициент надежности по нагрузке от собственного веса , а от временной нагрузки при может подсчитываться как

Откуда следует:

Динамический коэффициент оказывается для этого примера равным .

Найдем опасные значения напряжений в крайних волокнах каждой из двух арок:

Основное преимущество использованных при подсчете напряжений одночленных формул 3.7 заключается в том, что здесь существенно упрощается решение вопроса об отыскании наиболее "невыгодного" расположения временной нагрузки для получения экстремальных значений фибровых напряжений. Это упрощение достигнуто благодаря тому, что по (3.7) фибровое напряжение зависит только от одного вида усилий (или ) и, следовательно, каждый раз должна загружаться только какая-либо одна линия влияния. При использовании двучленной формулы

Нужно загружать две линии влияния (и) одновременно, что усложняет нахождение положения нагрузки, вызывающей наименьшее или наибольшее значение фибрового напряжения.

3.2 Построение линий влияния усилий в сечениях трехшарнирных рам

Трехшарнирные рамы относятся к распорным системам, и поэтому построение линий влияния усилий в таких рамах во многом аналогично построению линий влияния усилий в трехшарнирных арках.

Для рамы, показанной на рис. 3.11, а л.в. вертикальных составляющих опорных реакций строятся как в балке с консолями (см. рис. 3,11, б), а для

Л.в. N_К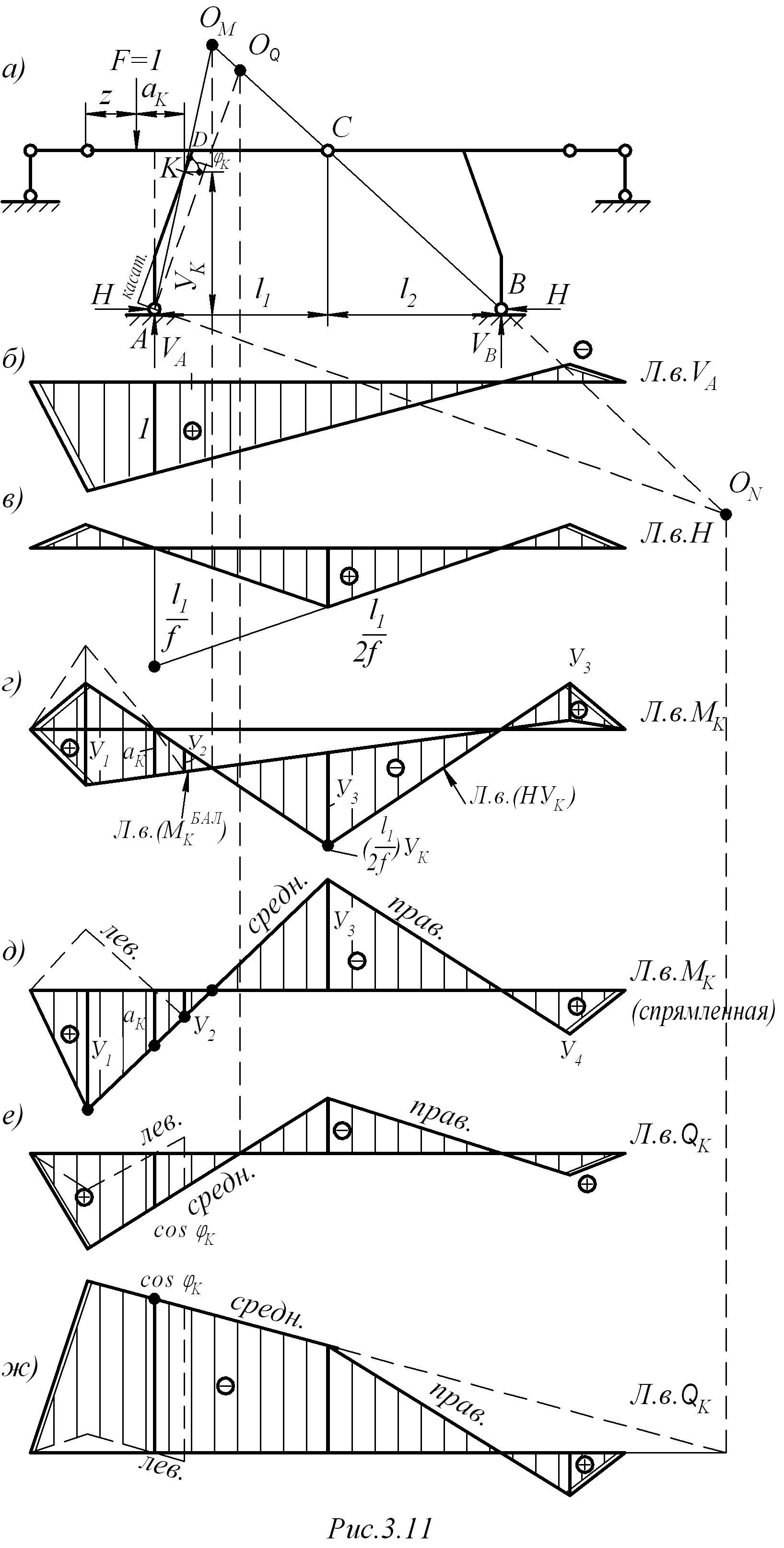

построения л.в. распора используется выражение л.в. л.в. , т.е. очертание этой л.в. (рис. 3.11, в) с точностью до множителя повторяет очертание линий влияния балочного изгибающего момента в сечении .

Линии влияния внутренних усилий в сечениях, расположенных между опорами трехшарнирной рамы, строятся так же, как в арках без консолей, с последующим продлением левой ветви до конца левой консоли, а правой ветви - до конца правой консоли. Если к консолям присоединены дополнительные шарнирные балочки (подвесные пролеты), то (по правилу учета узловой передачи нагрузки) ординаты на концах консолей соединяются прямыми с нулевыми ординатами на опорах подвесных пролетов.

Для сечений, расположенных на консолях рамы, линии влияния усилий (M, Q) строятся как в отдельно рассматриваемых консольных балках.

Внутренние усилия в сечении с координатами центра тяжести , и углом наклона касательной к горизонту определяются приведенными выше формулами (3.1). Воспользуемся описанным в п. 3.1.2 способом наложения. На рис. 3.11, г л.в. совмещена с л.в. распора Н, ординаты которой умножены на . В результате в суммарной л.в. ордината получается как сумма абсолютных величин ординат суммируемых линий влияния, а определяются вычитанием соответствующих ординат. Откладывая эти ординаты от нулевой линии (положительные - вниз, отрицательные - наверх), получаем окончательный вид л.в. (рис. 3.11, д).

Линии влияния поперечных и нормальных сил в том же сечении приведены на рис. 3.11, е, ж.

Рассмотрим построение тех же линий влияния с использованием нулевых точек . Точка находится (как и в трехшарнирной арке) в результате пересечения линий и (т.е. линий действия опорных реакций и при условии, что сила находится на среднем участке и ).

Точка лежит на пересечении линии действия реакции , проведенной параллельно касательной к оси рамы в точке , и опять-таки линии . Наконец, пересечением с линией действия , перпендикулярной к касательной к оси рамы в точке , определяется положение точки .

Переходим непосредственно к построению линий влияния усилий.

Линия влияния (см. рис. 3.11, д и 3.12, д). Сносим нулевую точку на горизонтальную ось. Через полученную точку и вершину опорного отрезка длиной , отложенного вниз под опорой , проводим среднюю прямую. Правая ветвь получается соединением ординаты под шарниром с нулем под опорой , а левая (показанная на рис. 3.11, д штрихами) - соединением точки под сечением с нулем под опорой . При наличии консолей обе крайние ветви продлеваются до конца консолей и затем соединяются с нулями на опорах правого и левого подвесных пролетов (соответствующие передаточные прямые показаны двойными линиями).

Примечание. На рис. 3.11, г-ж левые (штриховые) ветви недействительны,

так как сила, находящаяся на консоли, передает свое действие на раму в узле правее сечения . Поэтому средние ветви продлеваются влево до конца консоли (как в л.в. ).

Линия влияния . На рис. 3.11, е и 3.12, е нулевые точки оказались в разных местах: в первом случае находится на среднем участке выше линии BC, а во втором совпала с опорой B.

Дальнейшие построения во многом повторяют аналогичные построения для арки. Под опорой откладывается вниз отрезок длиной , и его конец соединяется с нулевой точкой. Способ получения левой (штриховой на рис. 3.11, е) и правой ветвей очевиден из чертежа. Для рис. 3.11, е штриховые линии недействительны (см. примечание к описанию построения л.в. ).

Линия влияния (см. рис. 3.11, ж и 3.12, ж). Для рамы по рис. 3.11, нулевая точка определяется пересечением с перпендикуляром к касательной к оси рамы в точке . Под опорой откладывается вверх отрезок длиной , и его конец соединяется с проекцией точки на ось л.в. Дальнейшее очевидно из чертежа, причем и в этом случае левая (штриховая) ветвь недействительна (см. примечание к описанию построения л.в. ). Точка для рамы по рис. 3.12 оказалась над опорой , в связи с чем ее нельзя использовать для установления направления средней линии. В соответствии с третьей из формул (3.1) в данном случае, при , имеем:

л.в. л.в.л.в. л.в. , т.е. искомая линия влияния есть "перевернутая" л.в. распора .

Построение л.в. и для сечений на консольной части рамы (рис. 3.12, з и 3.12, и). Пусть сила находится на консоли правее сечения . Тогда , причем , а , т.е. л.в. и совпадают с линиями влияния усилий в сечении консольной части обычной балки (с подвесными пролетами).

Перейдем теперь к построению линий - влияния усилий в сечении, расположенном на правой части рамы (рис. 3.13). Порядок построения остается в принципе прежним, но нужно иметь в виду, что, строя л.в. , мы теперь должны опорный (правый) отрезок длиной откладывать вверх (т.е. со знаком минус, как на рис. 3.13, е).

Так как лучи и в данном примере совпадают, то для сечений и оказалась общей нулевая точка линии влияния изгибающего момента. Различие между л.в. и л.в. состоит в величине отрезков и , откладываемых вниз под правой опорой, и в ограничении правых ветвей вертикалями, проводимыми под сечениями и соответственно. Эти л.в. показаны на рис. 3.13, б и 3.13, д.

Так как нулевая точка линии влияния поперечной силы в сечении оказалась над правой опорой, то построение выполняется в соответствии с формулами (3.1) при :

л.в. л.в.л.в. л.в. ( л.в. совпадает с «перевернутой» л.в. распора, см. рис. 3.13, в).

Нулевая точка для л.в. поперечной силы в сечении совпала с точкой , поэтому средняя ветвь (I левая) является продолжением II левой. Так как , то опорный отрезок имеет длину . Как уже отмечалось, для сечения на правой части рамы этот отрезок откладывается вверх от оси л.в. (рис. 3.13, е).

Рассмотрим, наконец, построение л.в. нормальной силы (рис. 3.13, г). Нулевая точка совпадает с опорой . И в этом случае I левая ветвь является продолжением II левой. Длина опорного (правого) отрезка равна . Что касается л.в. , то поскольку нулевая точка оказалась над правой опорой, снова приходится обращаться к использованию формул (3.1) при:

л.в. л.в.л.в. л.в. , т.е. линия влияния л.в. полностью совпадает с л.в. (см. рис. 3,13, ж).