14.4.3 Третье единичное состояние

Третье единичное состояние вызвано действием пары моментов в узле (рис. 14.6). Строим эпюру изгибающих моментов на участ­ке . Дальнейшая последовательность решения следующая.

1. Из условий равновесия балки определяются действующие в ней поперечные силы

2. Рассматривается равновесие узла и определяется опорная ре­ акция

3. Определяются поперечные силы в балке

4. Из равновесия узла определяются усилия в ванте (продольная сила ) и продольная сила в балке жесткости . При определении направления действия следует иметь в виду, что в опоре нет горизонтальной связи и, следовательно, не может возникнуть горизонтальной опорной реакции, а на участке - продольной силы. Таким образом, сила полностью переходит из узла на участок .

5. Из равновесия узла О определяются силы и .

6. Определяется опорная реакция, действующая в опоре (из равновесия узла ), и усилие в ванте .

7. Опорная реакция и усилие в ванте - из равновесия узла .

8. Усилие в ванте вызывает изгиб балки жесткости на участке . Строим эпюру изгибающих моментов.

9. Определяются поперечные силы в балках и .

10. Из равновесия узла определяем опорную реакцию .

Проверка общего равновесия всей системы:

14.5 Построение эпюр и от вертикальной единичной силы

В качестве загружения системы необходимо рассмотреть состояния, возникающие вследствие приложения единичной вертикальной силы в различных позициях (позиции приложения силы указаны в заданиях треугольниками, см. рис. 14.1). Последовательность построения эпюр и аналогична рассмотренным выше единичным состояниям.

Пример грузового состояния приведен на рис.14.7 (сила приложена в узле ). Последовательность построения эпюр следующая.

1. Рассмотрим равновесие узла . Сила приложена в шарнире и, следовательно, не вызывает изгиба в балке , а только растягивает ванту и сжимает балку проезжей части. Отметим также, что продольная сила на участке возникнуть не может, так как в опоре нет горизонтального закрепления. А на участке действует только продольная сила (поперечных сил здесь нет, так как нет изгиба). Таким образом:

2. Узел . Так как ванты и наклонены под одним углом к горизонтали (оси ), то усилия в них одинаковы и равны Определим опорную реакцию :

На рис.14.7 приведены также варианты определения усилий в узлах и при помощи силовых треугольников.

3. Усилие в ванте изгибает балку (здесь ситуация аналогична рассмотренному выше третьему единичному состоянию). Строим эпюру изгибающих моментов на данном участке балки от вертикальной составляющей усилия .

4. Балка . В крайнем левом сечении балки (длиной ) действует изгибающий момент, равный , который уравновешивается парой поперечных сил 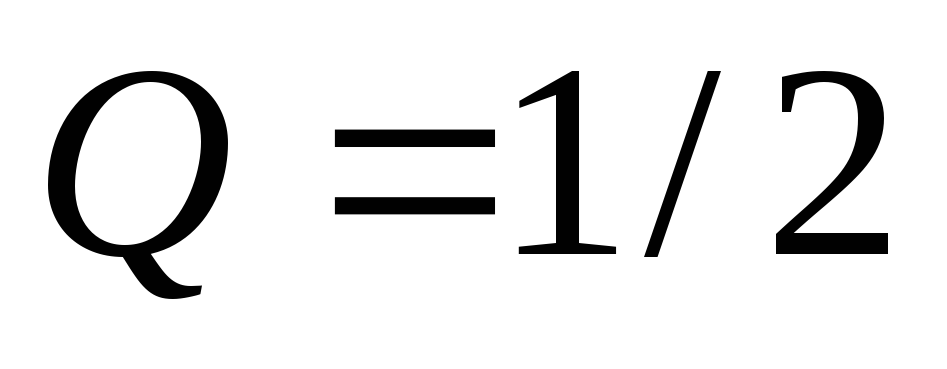; наряду с поперечными силами действует продольная сжимающая сила (перешедшая в балку из узла ).

5. Балка АВ. Определим поперечные силы в балке :

6. Узел . Все силы, действующие в узле , уже определены, осталось только проверить их равновесие:

7. Узел А. Из уравнения равновесия проекций всех сил на вертикальную ось определим опорную реакцию .

Общее равновесие всей системы в данном случае очевидно.