9.2.4 Проверка равновесия фермы

Определим составляющие опорных реакций по осям для заданной системы при нагружении внешней нагрузкой и нагружении единичными усилиями по направлению искомых перемещений .

Вычисления производим в табл. 9.4 (от силы ) и 9.5 (от силы ).

Таблица 9.4

Узел	Усилие	Проекции реактивных сил на оси
9		0,08203 0,73117	-0,08203 -0,08125	-0,6562 -0,6500
10		0,01172	0,08202	-0,09374
11		0,01173	-0,01173	0,09379
12		0,17502 0,01173	0,17502 0,08208	1,400 0,09381
	Внешние силы
	Погрешность, %	0,006	0,013	0,004

Таблица 9.5

Узел	Усилие	Проекции реактивных сил от на оси
9		-0,07497 -0,7200	0,07497 0,0800	0,59968 0,6400
10		0,075 0,080	0,525 0,080	-0,600 -0,640
11		0,720 0,075	-0,080 -0,075	0,640 0,600
12		-0,080 -0,075	-0,080 -0,525	-0,640 -0,600
	Погрешность, %	0,003	0,003	0,013

Таким образом, выполнены условия равновесия фермы при нагружении внешней силой и единичными .

9.2.5 Определение перемещений узлов фермы

Для определения перемещений в ферме используем формулу Мора

учитывающую продольные силы в каждом стержне фермы от единичных сил и внешних нагрузок, которые в пределах длины каждого стержня и жесткость постоянны.

Где - усилия во всех стержнях фермы от внешней силы в заданном узле;

- усилия во всех стержнях фермы от единичных сил, приложенных в узлах по направлениям искомых перемещений;

- модули продольной упругости стержней;

- площади поперечных сечений стержней.

Запишем выражения для определения следующих перемещений:

Произведения вычисляются в табл. 9.3 по столбцам 11,13 и записываются в столбец 14; тогда сумма дает: .

Произведения вычисляется в табл. 9.3 по столбцам 10, 11 и 13 и записывается в столбец 15, получаем: .

Произведения вычисляются в табл. 9.3 по столбцам 10, 13 и записываются в столбец 16. Перемещение вычисляется как сумма столбца 16, тогда имеем: .

Домножив найденные единичные перемещения , и на соответствующие значения заданных сил вычислим действительные перемещения узлов фермы.

1. взаимное перемещение узлов 6 и 8 от одинаковых сил, приложенных в этих узлах навстречу друг другу вдоль линии, проходящей через эти узлы;

2. домножив на , получим взаимное перемещение узлов 6 и 8 но от силы 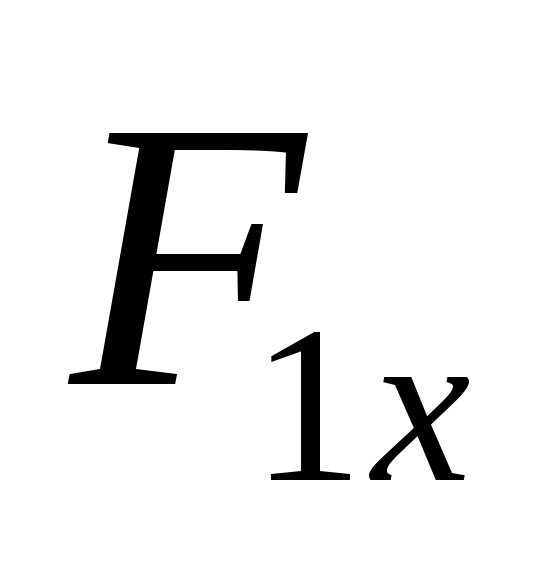, приложенной в узле 1;

3. умножив на перемещение получим перемещение узла 1 по направлению силы

Найдем численное значение последнего перемещения при: , где для трубы (труба квадратная ГОСТ30245-2003).

Подставив численные значения (при условии, что труба не теряет устойчивость), получим

Окончательный контроль результатов расчета. Определяем составляющие опорных реакций по осям для заданной системы при нагружении внешними силами. Вычисление проекций реакций на оси производим в табл. 9.6 от .

Таким образом, выполнены условия равновесия заданной фермы по уравнениям , , .

Необходимо также проверить выполнение трех уравнений моментов, например относительно осей , и :

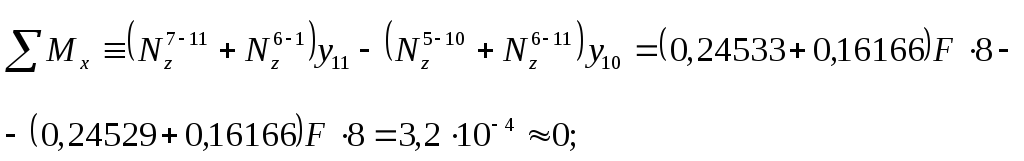
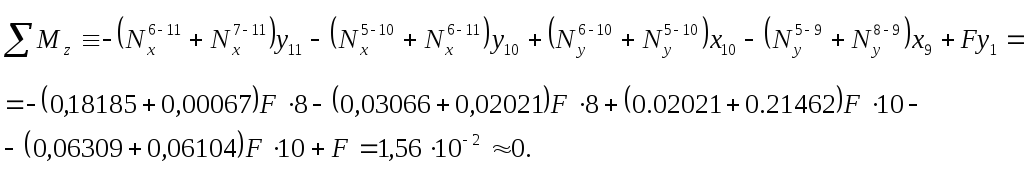
Наиболее точно выполняется последнее уравнение - с погрешностью .

Таким образом, выполнение шести уравнений статического равновесия фермы достаточной точностью показывают, что расчет выполнен правильно.

Таблица 9.6

Узел	Усилие	Проекции реактивных сил на оси
9		0,06309 0,54932	-0,06309 -0,06104	-0,50466 -0,48833
10		0,03066 0,02021	0,21462 0,02021	-0,24529 -0,16166
11		0,18185 0,03067	-0,02021 -0,03067	-0,16166 0,24533
12		0,15481 -0,03066	0,15481 -0,21462	1,400 0,09381
	Внешние силы
	Погрешность, %	0,3	0,003	0,01