Ещё один архив по мостам и строительству / 1-6 семестр / строймех 2 / Глава_4

Глава 4. Определение перемещений в плоских рамах от внешних нагрузок.

4.1. Формулы используемые для определения перемещений

Формула Мора для плоской системы состоит из трех интегралов

(4.1)

где - перемещение по направлению i-ой единичной силы, вызванное внешней нагрузкой - внутренние усилие от i-ой единичной силы; - внутренние усилия от нагрузки - жесткости элементов рамы соответственно при: изгибе, продольной деформации и сдвиге: k - коэффициент учитывающий неравномерность распределения по сечению касательных напряжений.

В этом случае когда одна из эпюр линейная и жесткости в пределах линейных участков эпюр постоянны используют - прием Верещагина.

(4.2)

где - площади эпюр от внешних нагрузок соответственно при изгибе, продольной деформации и сдвиге;

- ординаты в соответствующих эпюрах от единичных сил, приложенных в сечениях по направлению искомых перемещений, но взятых под центрами тяжести соответствующих грузовых эпюр.

В приближенных вычислениях перемещений в балках и рамах учитывают только первый интеграл:

(4.3)

При вычислении перемещений в фермах учитывают только второй интеграл:

(4.4)

Вычисления перемещений по формулам (4.2, 4.3) называют «перемножением» эпюр.

Часто приходится «перемножать» сложные эпюры в том числе и криволинейные. Сложные эпюры разбивают на участки. В пределах каждого участка можно применить либо формулу Мора-Верещагина (если известны центры тяжести площади) или формулу трапеций - для линейных эпюр, либо формулу Симпсона, если одна из эпюр криволинейная (рис. 4.1).

- формула трапеций для одного участка:

(4.5)

- формула Симпсона:

(4.6)

Во всех формулах при перемножении эпюр перед каждым произведением ординат ставится знак минус если ординаты разнозначные.

Следует отметить, что формула Симпсона наиболее удобна и универсальна, заменяя предыдущие.

4.2. Пример. В заданной раме рис. 4.2 определить перемещения: в сечении Д – горизонтальное, в сечении Т – вертикальное и в сечении В – угловое.

Из формул, перечисленных выше, следует, что для определения любого перемещения необходимо построить две эпюры - одну от заданных сил, другую от единичной силы, приложенной в сечении, в котором ищут перемещение. Если рама статически неопределима, то одна из эпюр должна быть построена в статически неопределимой системе. Нам необходимо построить три эпюры от единичных сил и одну от внешних нагрузок.

Для построения эпюры от внешних сил найдем из уравнений статики в заданной раме (рис 4.2) опорные реакции

1) ;

2) ;

3)

Проверка: ;

Аналогично найдены опорные реакции во всех единичных состояниях рамы. Эпюры изгибающих моментов строят по значениям моментов, найденным в характерных сечениях рамы (опорах, узлах, местах приложения сосредоточенных сил, моментов, а также в начале, середине и конце распределенной нагрузки). Буквами H,C,K обозначены соответственно: начало, середина и конец участка (рис 4.3), а цифрами - номера участков.

Построение эпюры :

Участок 1:

Участок 2:

Полученные ординаты отложены со стороны растянутых волокон (рис. 4, а-г). Аналогично построены единичные эпюры. Используя эпюры (рис. 4.4) можно найти перемещения. Для определения горизонтального перемещения сечения Д эпюры (рис. 4.4 а, б) разделены на три участка, и для каждого из них применены формулы Симпсона или трапеций.

при имеем:

«Перемножив» эпюры и (рис. 4а, в), получим вертикальное перемещение сечения «Т».

Знак минус говорит о том, что перемещения сечений и происходят в сторону противоположную направлениям и .

Для определения угла поворота «перемножим» эпюры и (рис. 4, г).

Знак «+» говорит о том, что сечение В повернулось в сторону вращения , т.е. по ходу часовой стрелки.

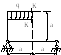
4.3 Задания для расчетно - проектировочных работ по теме «Определение перемещений в рамах».

В заданном сечении «К» рамы определить угловое и линейное перемещение при . Данные взять из табл. 4.1 и рис. 4.5.

Таблица 4.1

строка	a	F	q	m	строка	a	F	q	m
	м	кН	кН/м	кНм		м	кН	кН/м	кНм
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	1.2 1.4 1.6 1.8 2.0 2.2 2.4 2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0	24 23 22 21 20 19 18 17 16 17 16 15 14 13 12	8 7 6 5 4 3 2 3 2 6 1 2 5 2 3	12 8 10 9 15 18 14 16 20 10 12 8 14 16 18	16 17 18 19 20 21 22 23 24 25 26 27 28 29 30	5.2 5.1 5.0 4.9 4.7 4.5 4.3 4.1 3.9 3.7 3.5 3.3 3.1 2.9 2.7	10 11 13 15 17 19 21 23 25 27 29 31 33 35 36	9 10 12 14 16 15 14 13 12 11 10 9 8 7 6	15 12 10 9 6 8 12 15 18 14 16 20 10 12 14

Рис. 4.5

5