Глава 13. Расчет неразрезных балок на жестких опорах

13.1 Состав задания

1 . Для заданной на рис. 13.1 балки необходимо определить следующие усилия от воздействия нормативной вертикальной нагрузки К-14:

а) максимальное положительное значение изгибающего момента в середине 3-го пролета ;

б) минимальное отрицательное значение изгибающего момента над опорой "В" ;

в) минимальное отрицательное значение перерезывающей силы в поперечном сечении балки, расположенном бесконечно близко слева от опоры "В";

г) максимальное положительное значение опорной реакции в опоре "В".

2. Построить эпюры и в балке, вызванные смещением вниз опоры "В" на величину, равную .

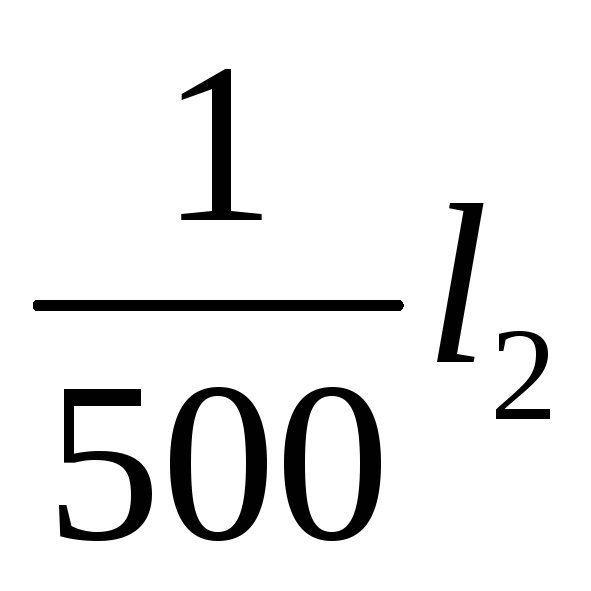В качестве исходных данных для расчета принимаем:

.

Примечание: Исходные данные для задания см.п. 13.5

Решение задачи состоит из двух частей.

Решение первой части выполняется в следующей последовательности:

• с помощью кинематического метода строятся модели линий влияния усилий , , , ;

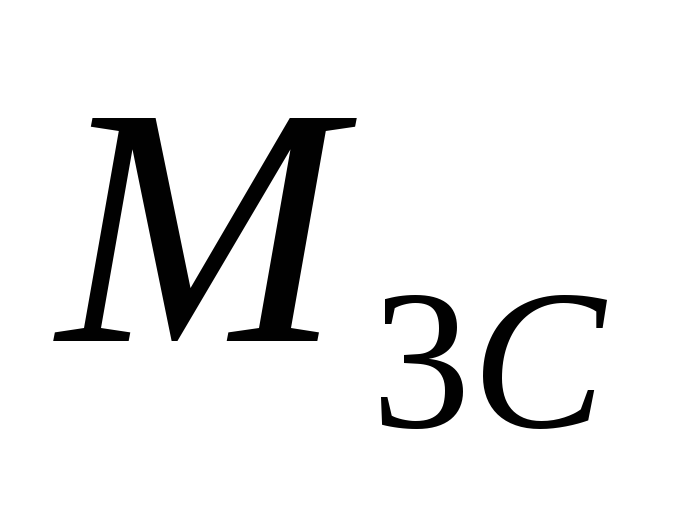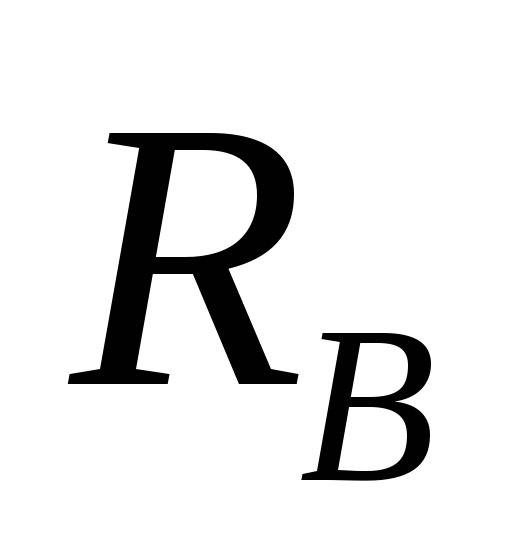• по моделям линий влияния определяются расположение подвижной нагрузки и величина эквивалентной нагрузки для каждого из определяемых усилий (в результате получится четыре варианта загружения балки статической нагрузкой);

• производится расчет исходной балки методом сил для каждого из четырех загружений, установленных выше;

• по результатам расчетов определяются величины , , , .

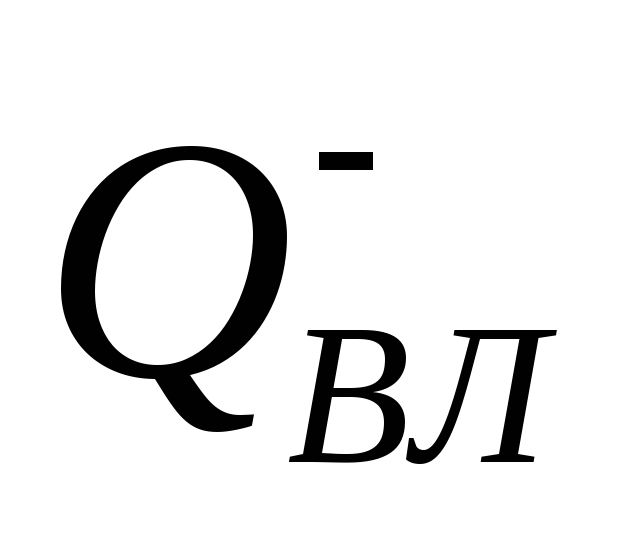Решение второй части задачи включает в себя расчет статически неопределимой балки методом сил на заданное смещение одной из опор.

13.2 Расчет неразрезной балки на временную подвижную нагрузку

13.2.1 Построение моделей линий влияния

Построим модель линии влияния (л.в.) усилия . Для этого в сечение балки, расположенное в середине третьего пролета "врезается", шарнир. Тем самым устраняется связь, препятствующая взаимным углам поворота сечений.

В направлении удаленной связи задается перемещение в виде единичного угла поворота (рис. 13.2, б), при этом направление углового перемещения противоположно направлению положительного момента в сечении (момент считается положительным, если растягивает нижние волокна балки); эпюра прогибов балки (изогнутая ось), вызванных таким воздействием, соответствует искомой модели л.в. (рис. 13.2, б).

Модель линии влияния строится аналогично , только шарнир в этом случае устанавливается над опорой "В" (рис 13.2, г).

Для построения модели л.в. в сечении, расположенном бесконечно близко слева от опоры "В", удаляется связь, препятствующая взаим­ным вертикальным перемещениям сечений. По направлению удаленной связи задается единичное перемещение в направлении, противоположном положительному (поперечная сила считается положительной если поворачивает отсеченную часть балки против часовой стрелки). Эпюра прогибов балки, вызванных этим перемещением, соответствует модели л.в. (рис. 13.2, е).

Для построения модели линии влияния удаляется опора "В". Вместо нее задается единичное вертикальное перемещение. Эпюра прогибов балки, вызванных этим перемещением, соответствует модели л.в. (рис. 13.2, з).

13.2.2 Определение эквивалентных нагрузкок

Определим расположение подвижной нагрузки и величины эквивалентных нагрузок для каждого из определяемых усилий.

Модель линии влияния показывает, что для получения максимального положительного значения изгибающего момента в середине 3-го пролета подвижную нагрузку необходимо расположить, над положительным участком модели л.в., т.е. в 3-м пролете балки (рис. 13. 2, а). Заменим криволинейное очертание модели линии влияния на этом участке тре­угольным, что позволит для определения величины эквивалентной нагрузки воспользоваться таблицей 13.1 эквивалентных нагрузок. В рассматриваемом случае получаем, что при , .

Как следует из модели л.в. , для получения подвижной нагрузкой надо загрузить 2-й и 3-й пролеты (рис. 13.2, в), т.к. в этих обоих проле­тах знак на модели л.в. отрицательный. Заменив криволинейное очертание модели л.в. на 2-м участке треугольным, получим, что при ,

.

Для загружения 3-го пролета значение эквивалентной нагрузки (при ).

Для определения подвижной нагрузкой загружаем 2-й и 3-й пролеты балки (рис. 13.2, д). При таком загружении для 2-го пролета (при ), а для 3-го (при ).

Для определения временной подвижной нагрузкой необходимо загрузить положительный участок модели л.в. , т.е. одновременно 2-й и 3-й пролеты (рис. 13.2, ж). Тогда , и .

Таким образом, определены схемы загружения исходной балки и значения эквивалентных нагрузок для получения каждого из определяемых усилий.