Глава 5 Расчет статически неопределимых рам методом сил

5.1 Последовательность расчета

1. Устанавливают степень статической неопределимости, выбирают основную систему (ОС) и лишние неизвестные.

2. Составляют канонические уравнения

3. Строят эпюры изгибающих моментов в основной системе от единичных неизвестных и заданной нагрузки.

4. Вычисляют коэффициенты и свободные члены канонических уравнений и выполняют их проверку.

5. Решают составленные канонические уравнения. Выполняют проверку их решения.

6. Строят эпюру изгибающих моментов и проверяют удовлетворение условий совместности деформаций.

7. Строят эпюры поперечных и продольных сил. Выполняют проверку эпюр , и по условиям равновесия всей рамы, а также отдельных ее частей.

8. Подбирают размеры поперечных сечений рамы.

5.2 О выборе основной системы метода сил

Статически неопределимой называется стержневая система (в частности, рама), внутренние усилия в которой не могут быть найдены исходя из одних только условий равновесия системы в целом или отдельных ее фрагментов. Степень статической неопределимости стержневой системы равна разности между минимальным числом силовых факторов, полностью определяющих ее напряженное состояние, и числом независимых уравнений равновесия этой системы. При расчете по методу сил различные варианты основной системы (ОС) получаются из заданной системы путем отбрасывания лишних связей (в количестве, равном степени статической неопределимости), т.е. связей, удаление которых не превращает систему в изменяемую.

Степень статической неопределимости плоской рамы (Н) может быть выражена через число замкнутых контуров (К) и число простых шарниров (Ш):

Н = ЗК-Ш.

Если в шарнирном узле сходятся более двух дисков (в частности, стержней), то шарнир называется сложным, для него принимается

где - число объединяемых шарниром дисков.

Рама, показанная на pис. 5.1. a, имеет три замкнутых контура - I, II, III (считается, что все опорные узлы принадлежат одному общему опорному диску - основанию). Возле каждого шарнирного узла обозначено число соответствующих простых шарниров. Заметим, что правая шарнирно - неподвижная опора эквивалентна одному простому шарниру, соединяющему два диска - стойку рамы и основание. Левый верхний шарнир называют неполным в том смысле, что он разрезает не все примыкающие к узлу стержни.

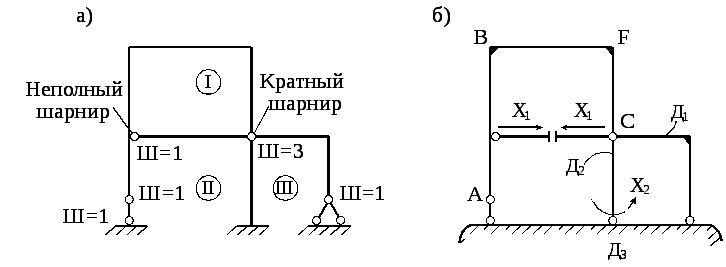
Рис. 5.1

Общее число простых шарниров для рассматриваемой рамы равно 7, поэтому (рама дважды статически неопределима) и соответствующие лишние неизвестные показаны на рис. 5.1, б Неизменяемость такой ОС следует из того, что правую ее часть можно рассматривать как три диска . Попарно соединенные тремя шарнирами, не лежащими на одной прямой, а левый диск ABFC присоединяется к правому при помощи шарнира С и левого опорного стержня, ось которого не проходит через этот шарнир.

Рама, изображенная на рис. 5.2, а, отличается тем, что у нее нет лишних опорных связей (все опорные стержни – абсолютно необходимые) и следовательно, рама внешне статически определима. Так как и , то . При этом разрез ригеля, являющегося перекрытием первого этажа, приводит к трем неизвестным метода сил (момент, поперечная и продольные силы), разрез ригеля второго этажа - к двум неизвестным (момент в шарнире равен нулю), а разрез ригеля третьего этажа - только к одному неизвестному (нормальной силе, поскольку в стержне с шарнирными концами при узловой нагрузке других усилий не возникает). Выбранная ОС (рис. 5.2, б) неизменяемая, т.к. представляет собой диск, соединенный с основанием тремя стержнями, не параллельными между собой и не пересекающимися в одной точке.

Если в процессе отбрасывания связей нарушаются правила образования неизменяемых систем, го такая расчетная схема не может использоваться в качестве ОС. Примером служат схемы 1, 2, 3 на рис. 5.3, а. В этих схемах опорные стержни пересекаются в одной точке или все параллельны между собой, что недопустимо, т.к. система оказывается мгновенно изменяемой. Допустимые (неизменяемые) варианты ОС представлены схемами 1,2,3 на рис. 5.3, б.

Рис. 5.3

На рис. 5.4, а и 5.5, а показаны рамы, обладающие упругой симметрией. В подобных случаях имеет смысл выбирать симметричную ОС и групповые неизвестные. Это приводит к разделению неизвестных: разрешающая система уравнений метода сил распадается на две подсистемы меньшего порядка – одна относительно только симметричных неизвестных, другая относительно кососимметричных. Если используется группировка неизвестных, то при выборе ОС отбрасывается взаимно симметричные связи и по их направлениям прикладываются как симметричные, так и кососимметричные группы сил. Симметричным групповым неизвестным соответствуют симметричные эпюры моментов в ОС, а кососимметричным групповым неизвестным – кососимметричные эпюры. Так, в ОС, показанной на рис. 5.4, б, силы и образуют симметричные группы, а группы сил и кососимметричные. В разрезе по оси симметрии действуют обычные (не групповые) неизвестные, причем - симметричные, - кососимметричное.

Рис. 5.4

Рис. 5.5

На рис. 5.5, б ОС получена введением двух дополнительных шарниров и разрезом средней стойки. Моменты в крайних опорах представлены своими симметричной и кососимметричной составляющими. Другой вариант ОС для той же рамы дан на рис. 5.5, в. Здесь - симметризованные и кососимметризованные вертикальные силы взаимодействия между средней стойкой и ригелями рамы.

Учащимся рекомендуется самостоятельно доказать, что схемы, приведенные на рис. 5.4, б и 5.5, б, в, геометрически неизменяемы.

5.3 Канонические уравнения метода сил

По своему физическому смыслу уравнения метода сил представляют собой условия совместности перемещений, т.е. выражают отсутствие в ОС перемещений по направлению отброшенных связей при действии усилий в этих связях и заданной нагрузки. Обычно эти уравнения записываются в стандартной (канонической) форме. В общем случае для раз статически неопределимой системы такая запись имеет вид

Здесь любой коэффициент - перемещение в ОС по направлению отброшенной связи с номером от действия едичного усилия в отброшенной связи с номером (то есть ); свободный (грузовой) член - перемещение в ОС по направлению связи с номером от заданной нагрузки.

В рамах и балках эти перемещения можно определить по одночленной формуле Мора – Верещагина (пренебрегая влиянием деформаций от действия продольных и поперечных сил) и др. см. ниже.

В этих формулах интегрирование выполняется по длине каждого участка рамы (балки), а суммирование - по всем участкам; и - площади эпюр изгибающих моментов в грузовом и единичных состояниях; - ордината эпюры , взятая под центром тяжести грузовой эпюры (в формуле для ) или единичной эпюры .

Некоторые характерные частные случаи применения правила Верещагина приведены на рис. 5.6. Наиболее универсальными являются «формула трапеций» (рис. 5.6, е) и формула Симпсона для «умножения» прямолинейной эпюры на квадратную параболу (рис. 5.6, д). Обе формулы могут применяться и в тех случаях, когда ординаты перемножаемых эпюр разнозначны. Нужно только иметь в виду, что каждое из произведений ординат положительно, если перемножаемые ординаты совпадают по знаку, и отрицательно в противоположном случае.

После решения канонической системы уравнений окончательные значения ординат эпюры изгибающих моментов определяются по формуле

.

По эпюре может быть построена (из условий равновесия отдельных участков рамы) эпюра поперечных сил . Эпюра нормальных сил обычно строится по эпюре исходя из условия равновесия узлов.

На каждом этапе вычисления и построения эпюр осуществляются соответствующие проверки.

Для детального изучения теоретических основ метода сил рекомендуется ознакомиться с соответствующей учебной литературой. При выполнении расчета рамы методом сил на ПЭВМ исходную информацию подготавливают в виде таблиц, составленных по определенным правилам. Читатели, желающие более глубоко, с современных позиций, осмыслить идеи методов расчета стержневых систем, могут обратиться к монографиям.

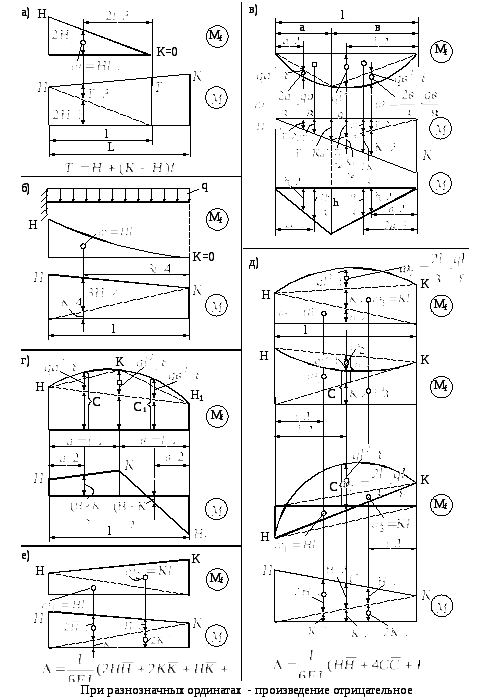
Рис. 5.6

5.4. Пример 1. Рассчитаем методом сил трижды статически неопределимую раму (рис. 5.7). Расчет начинается с выбора основной системы (ОС).

Для одной и той же рамы может быть предложено множество основных систем. Имеет смысл (при выполнении расчетов без применения ЭВМ) выбирать такие ОС, которые приводят к более простым эпюрам , и к меньшим объемам вычислений при определении , . На рис. 5.8 приведены три (симметричных) варианта ОС с соответствующими единичными и грузовыми эпюрами. Для дальнейшего рассмотрения принят первый вариант ОС.

Рис. 5.7