6.6 Проверка коэффициентов и свободных членов

Проверка правильности вычисления коэффициентов системы кано­нических уравнений метода перемещений выполняется аналогично про­верке коэффициентов уравнений при расчете рам методом сил.

Для этого строится суммарная единичная эпюра в основной системе алгебраическим суммированием всех единичных эпюр (рис. 6.20):

.

Рис. 6.20

Универсальная проверка состоит в том, что результат умноже­ния эпюры на эту же эпюру должен равнять­ся сумме всех коэффициентов системы канонических уравнений:

Перемножение эпюры «на себя» с применением приема Верещагина дает:

Коэффициенты вычислены правильно.

Проверка грузовых членов сводится к вычислению

Здесь - эпюра изгибающих моментов от внешней нагрузки в статически определимой системе метода сил, полученной из заданной системы устранением лишних связей (рис. 6.21, 6.22).

Рис. 6.21 Рис. 6.22

Степень статической неопределимости определена ранее .

Результат перемножения эпюры на эпюру должен равняться сумме всех грузовых членов в системе уравнений, взятых с противоположным знаком:

6.7 Решение системы канонических уравнений

Вследствие теоремы о взаимности реакций матрица системы канонических уравнений метода перемещения симметрична:

Решение системы уравнений целесообразно осуществить по правилу Крамера:

Проверка правильности решения системы канонических уравнений

1.

2.

3.

6.8 Построение эпюры изгибающих моментов

Эпюра изгибающих моментов в заданной статически неопределимой системе строится по результатам суммирования ординат эпюры , построенной в ОС метода перемещений от внешней нагрузки, с ординатами единичных эпюр, умноженных на найденные значения неизвестных :

.

Эпюры показаны на рис. 6.23, 6.24, 6.25.

Рис. 6.23 Рис. 6.24

На рис. 6.26 изображена эпюра .

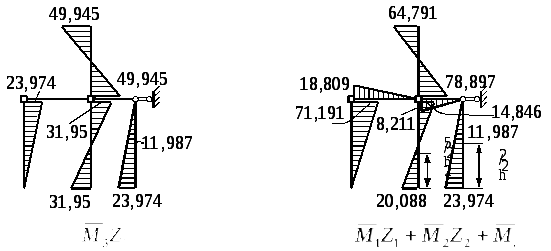
Рис. 6.25 Рис. 6.26

Эпюры изгибающих моментов строятся на растянутом волокне каждого участка рамы. Окончательная эпюра моментов представлена на рис. 6.27. На рис. 6.28 показано сложение эпюр и в стойке 3-6, где действует сосредоточенный момент .

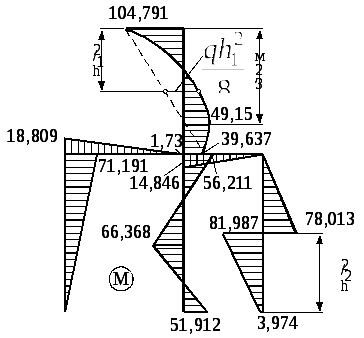
Рис. 6.27

Рис. 6.28

Проверка эпюры изгибающих моментов осуществляется двумя способами.

1. Статическая проверка: жесткие узлы рамы под действием приложенных к ним изгибающих моментов должны находиться в равновесии.

На рис. 6.29 показаны вырезанные узлы 1 и 2:

а)

б)

Рис. 6.29

2. Кинематическая проверка должна показать, что взаимные перемещения точек приложения сил Х_j (основная система метода сил рис. 6.21) по направлению этой силы Х_j в заданной раме равны нулю .

В примере рассмотрено определение вертикального перемещения в опоре 4, которое должно быть равно нулю. Для этого на рис. 6.30 построена единичная эпюра . По формуле Мора – Верещагина путем перемножения окончательной эпюры и получим:

Строго говоря, одной такой проверки недостаточно. Для полной уверенности в правильности построения эпюры число проверок должно быть равно степени статической неопределимости.

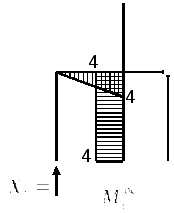
Рис. 6.30

6.9 Построение эпюры поперечных сил

Эпюры поперечных сил строятся по эпюре изгибающих моментов.

Поперечная сила может быть определена по формуле, выражающей одну из дифференциальных зависимостей при изгибе

.

Этой зависимостью удобно пользоваться в тех случаях, когда эпюра изгибающих моментов линейна. При этом соблюдается следующее правило знаков: поперечная сила положительна, если для совмещения оси элемента с касательной к эпюре изгибающих моментов приходится вращать эту ось по часовой стрелке. Вращение должно производиться так, чтобы угол поворота не превосходил .

Рис. 6.31

В стержне 2-7, на который действует равномерно распределенная нагрузка (рис. 6.31), поперечная сила определяется по формуле

где - поперечная сила в произвольном сечении шарнирной балки 2-7 от заданной нагрузки ,

- изгибающие моменты, действующие в узлах 2 и 7; взяты из эпюры (см. рис. 6.27);

При этом сохраняется принятое правило знаков и .

Экстремальный момент в стержне 2-7 (см. рис. 6.31) возникает в сечении, где производная функции , т.е. поперечная сила, обращается в ноль.

Эпюра поперечных сил рамы показана на рис. 6.32.

Рис. 6.32