6.4 Построение в основной системе, эпюр изгибающих моментов от единичных перемещений и от заданной нагрузки

Для определения коэффициентов и свободных членов системы канонических уравнений метода перемещений необходимо предварительно построить в основной системе эпюры изгибающих моментов от нагруз­ки и от единичных перемещений. Влияние продольных и поперечных сил обычно при этом не учитывается.

Построение эпюр производится при помощи специальных таблиц, в которых представлены эпюры изгибающих моментов от указанных воздействий в статически неопределимых балках двух типов: а) с двумя жесткими защемлениями; б) с одним защемленным, а с другим шарнирно опертым концом. Напомним, что основная система метода пе­ремещений состоит из совокупности независимо деформирующихся однопролетных статически неопределимых балок.

При построении единичных эпюр целесообразно предварительно нанести на схему рамы изогнутую ось каждого стержня, образован­ную заданным единичным смещением (или , или ), что позволит установить положение растянутых волокон и правильно изобразить эпюру моментов (рис. 6.4, 6.6, 6.8), на растянутых волокнах.

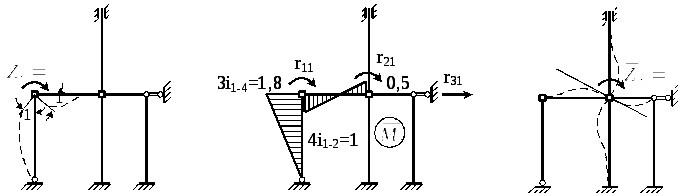
Рис. 6.4 Рис. 6.5 Рис. 6.6

Перед построением единичных эпюр необходимо определить погонные жесткости стержней

Нумерация узлов показана на рис. 6.3, а соотношение изгибных жесткостей на рис. 6.1. Для упрощения вычислений во всех погонных жесткостях примем .

На рис. 6.5, 6.7, 6.9 изображены эпюры , построенные в ОС при помощи специальных таблиц, которые представлены в каждом учебнике по строительной механике.

Рис. 6.7 Рис. 6.8 Рис. 6.9

Эпюра в основной системе от заданной нагрузки строится на трех стержнях рамы, несущих внеузловую нагрузку.

1. Балка 2-7 с двумя заделанными концами, где действует равномерно распределенная нагрузка . При помощи таблиц определяются моменты в заделках по формуле

2. Балка 2-5 с двумя заделанными концами, при действии сосредоточенной силы (рис. 6.10).

Рис. 6.10 Рис. 6.11

По условию тогда

Из табл. изгибающий момент на опоре 2

на опоре 5

Изгибающий момент в стойке 2-5 под силой вычисляется по формуле

Опорные реакции в статически неопределимой стойке 2-5 находим также при помощи табл.:

Проверка:

Целесообразно сделать проверку правильности определения реакций через эпюру , построенную по эпюре :

3. Балка 6-3 с заделкой на одном конце и шарнирной опорой на другом, загруженной сосредоточенным изгибающим моментом (рис. 6. 11).

По условию поэтому .

Из табл. момент на опоре 6

Изгибающий момент в сечении , где приложен заданный

. В сечении, где действует в эпюре - скачок на . Реакции вычисляются по формуле

.

Для проверки построим эпюру , по эпюре (см. рис. 6.11).

; .

Проверка выполнена, значения совпали с ординатами эпюры .

Эпюра , построенная в ОС после приведенных выше вычислений, изображена на рис. 6.12.

Рис. 6.12

6.5 Определение коэффициентов и свободных членов канонических уравнений

Статическим способом коэффициенты и свободные члены определяются из условий равновесия всей рамы или ее частей, содержащих введенные связи.

Все коэффициенты и свободные члены делятся на две группы:

1. коэффициенты и свободные члены, представляющие реактивные моменты во введенных заделках, определяемые вырезанием узлов и составлением уравнений равновесия вида

2. коэффициенты и свободные члены, представляющие реактивные усилия во введенных опорных стержнях, определяемые при помощи рассечения рамы на две части либо из рассмотрения равновесия всей рамы с учетом заданных сил и опорных реакций, и составления уравнений равновесия сил, действующих на отсеченную часть, .

Реактивное усилие считается положительным, если направление его действия совпадает с принятым направлением поворота или линейного смещения узла.

На рис. 6.13 показано определение реактивных моментов в свя­зи 1 от единичных смещений ,,. В соответст­вующих единичных состояниях с эпюрами вырезается узел 1 вместе с введенной в него "плавающей заделкой" (связью 1).

В зависимости от положения растянутых волокон, показанных пунк­тиром, определено направление действующих на узел 1 изгибающих моментов.

а) (при определении следует обратить внимание на то, что все слагаемые, образующие - положительные);

б)

в)

Рис. 6.14 иллюстрирует определение реактивных моментов во второй связи из условия равновесия узла 2:

а)

б)

в)

Реактивный момент определяется из условия равновесия узла 1 в грузовом состоянии, - из условия равновесия узла 2 (рис. 6.15):

а)

б)

Реакции в дополнительном опорном стержне (связь 3) определяются из условия равновесия рамы, освобожденной от опор.

Рис. 6.13 Рис. 6.14 Рис. 6.15

На рис. 6.16, 6.17, 6.18, 6.19 показаны расчетные схемы для определения реакций в дополнительном стержне. Горизонтальные реакции опор в единичном состоянии основной системы определяются также при помощи таблиц.

В первом единичном состоянии (рис. 6.16)

Рис. 6.16 Рис. 6.17

Во втором единичном состоянии (рис. 6. 17)

В третьем единичном состоянии (рис. 6.18)

Рис. 6.18 Рис. 6.19

Взаимность реакций имеет место: ;

Грузовое состояние представлено на рис. 6.19, показаны горизонтальные реакции в опорах, вычисленные ранее при помощи таблиц.

Выражение суммы проекций всех сил в том числе и заданных, приложенных к раме, на горизонтальную ось имеет вид:

На ось проектируются все силы, действующие на раму: не только горизонтальные реакции в опорах от внешней нагрузки, но и активная нагрузка .