17.3. Расчет статически неопределимых рам со смещающимися опорами
Статически неопределимые стержневые конструкции обладают следующей особенностью. Внутренние усилия в них возникают не только от внешней нагрузки, но и от осадки опор, неточности изготовления отдельных элементов, изменения температурного режима, тогда как в статически определимых системах все эти факторы вызывают лишь перемещения отдельных точек. Деформация при этом отсутствует. Это на первый взгляд отрицательное свойство статически неопределимых систем может быть использовано в расчетах для регулирования усилий в отдельных элементах с целью получения оптимальной конструкции.
Регулирование происходит за счет наложения усилий от внешней нагрузки на усилия от осадки опор, монтажные усилия.
Расчет статически неопределимых рам на смещение опор можно производить как методом сил, так и методом перемещений. Для выбора метода расчета необходимо определить степень статической и кинематической неопределимости и выбрать более простой метод.
17.3.1
Задача 1.
В раме, изображенной на рис. 17.10, а,
правая опора
повернулась на угол
.
Определить внутренние усилия в раме.
Решение. Степень
статической неопределимости
.
Степень кинематической
неопределимости
.
Рис. 17.10
Для расчета выбираем метод сил. В этом случае целесообразно использовать теорему о взаимности возможных работ.
Выбранная основная система рассматривается в двух состояниях -действительном и единичном. Работа сил действительного состояния на соответствующих им перемещениях единичного должна быть равна работе сил единичного состояния на соответствующих им перемещениях действительного.
Основная система
представлена на рис. 17.10, б.
Это рама, у
которой убрана моментная связь в заделке.
Неизвестный момент
должен быть
такой, чтобы сечение над правой опорой
повернулось на заданный угол
.
Назовем состояние системы на рис. 10, б
действительным.
В единичном состоянии отброшенная связь
заменяется моментом
.
Соответствующее смещение обозначается
(рис.17.10, в).
На основании теоремы о взаимности возможных работ записываем:
Если неизвестная реакция совпадает по направлению с перемещением, то перед слагаемым ставится знак плюс, если противоположна - минус. Решая уравнение, находим:
Для определения
используется формула Мора - Верещагина
(рис. 17.11, а)
Результирующая
эпюра
показана на
рис. 17.11, б.
Она получена из единичной эпюры, все
ординаты которой умножены на
.
Рси. 17.11
17.3.2
Задача 2.
В раме (рис. 17.12, а),
загруженной распределенной нагрузкой
,
произошло
вертикальное смещение левой опоры на
величину
.
Определить внутренние усилия с учетом
смещения опоры. Построить эпюры внутренних
усилий при
.
Решение. Если смещение опоры происходит в раме, к которой приложена внешняя нагрузка, то расчет лучше производить отдельно от осадки и от внешнего воздействия, после чего результаты сложить.
Рис. 17.12
На рис. 17.12, б,
в показана
основная система. Здесь
- неизвестная
реакция в отброшенной связи от внешней
нагрузки,
-
то же, от
смещения опоры
.
Для определения
используем теорему
о взаимности возможных работ (17.12, в,
г):
Для определения
запишем уравнение
метода сил (рис.
17. 12,
г,
д):
Для получения
результирующей эпюры моментов (рис.
17.13, а)
можно воспользоваться формулой
Рис. 17.13
При отсутствии
осадки опоры
результирующая эпюра моментов получится
по формуле
(рис. 17.13, б).
В статически неопределимых системах, зная внешнюю нагрузку, можно смещением опор добиться равенства максимальных моментов в различных сечениях, то есть отрегулировать усилия.
17.3.3
Задача 3.
Для рассмотренной выше задачи найдем
такое значение
,
при котором изгибающий момент в узле и
в середине горизонтального стержня
будут одинаковыми (см. рис. 17.13, б).
Решение. Эпюра
только от осадки опоры на величину
представлена на рис. 17.14.
Рис. 17.14
На рис. 17.15 представлена оптимальная эпюра изгибающих моментов.
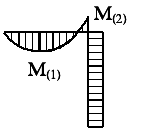
Рис. 17.15
Если степень статической неопределимости больше степени кинематической неопределимости, то раму лучше рассчитывать методом перемещений.
17.3.4
Задача 4.
Определить усилия в раме (рис. 17. 16, а)
от поворота правой опоры на угол
.
Решение. Рама два раза статически и один раз кинематически неопределима. Основная система представлена на рис. 17.16, б. Каноническое уравнение метода перемещений запишется в виде:
здесь
- реакция в добавленной связи от ее
единичного поворота (рис. 17.16, в),
- реакция
в добавленной связи от заданного
углового смещения (17.17, а,
б),
Эпюра
получится
сложением эпюр
,
и
(рис. 17.18).
Рис. 17.16
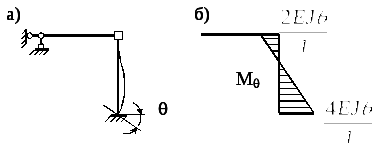
Рис. 17.17
Рис. 17.18