9.2 Основное дифференциальное уравнение неравномерного движения воды.

Рассмотрим вначале общий случай – случай нецилиндрического русла. При этом будем иметь в виду (как здесь, так и всюду ниже) случай «безотрывного» плавно изменяющегося движения воды в русле (случай, когда водоворотные области не образуются и живые сечения принимаются плоскими).

Представим на рис. 9.8 продольный разрез потока, находящегося в состоянии неравномерного движения. Оси координат для построения кривой свободной поверхности наметим, как показано на чертеже: ось глубин h – вертикально; ось s – по линии дна русла.

Рис. 9.8. К выводу дифференциального уравнения неравномерного движения.

Возьмём два плоских вертикальных живых сечения потока: 1-1, удалённое от начального сечения W-W на конечное расстояние s, и 2-2, расположенное от 1-1 на бесконечно малом расстоянии ds.

Обозначим потерю напора на длине ds потока (при неравномерном движении) через dh_l. Очевидно, величину dh_l можно представить в виде

где гидравлический уклон

или

причем здесь z – возвышение точки А свободной поверхности над плоскостью сравнения ОО; – средняя скорость в первом сечении; - корректив кинетической энергии, который условно будем принимать равным , т.е. таким же, как и для равномерного движения.

Подставив (9.3) в (9.1), имеем

Вводя теперь обозначение

переписываем (9.4) в виде

Это и есть основное уравнение неравномерного движения, причём здесь dz представляет собой поднятие свободной поверхности АВ на длине ds (dz может быть как положительным, так и отрицательным, на рис. 9.8 dz имеет отрицательное значение, а следовательно, представляет собой падение свободной поверхности).

Из (9.6) видно, что падение свободной поверхности, т.е. уменьшение удельной потенциальной энергии, равно изменению удельной кинетической энергии плюс потеря напора.

Разделим уравнение (9.6) на величину ds:

Так как в случае безнапорного движения пьезометрическая линия Р-Р совпадает со свободной поверхностью, то

где I – пьезометрический уклон.

Величину , входящую в (9.7), т.е. гидравлический уклон I_e часто представляют в виде

где i_f – иногда называют уклоном трения. Учитывая (9.8) и (9.9), уравнение (9.7) переписываем в виде

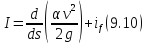
Далее используем следующее допущение:

считаем, что потери напора при плавно изменяющемся и безотрывном движении воды выражаются теми же зависимостями, что и в случае равномерного движения воды.

В соответствии с этим допущением величину i_f выражаем, пользуясь формулой Шези (справедливой, строго говоря, только для равномерного движения):

где , С, R и K относятся к рассматриваемому сечению 1-1.

Учитывая (9.11) и полагая , окончательно получаем

Уравнение (9.12) является первым видом дифференциального уравнения неравномерного движения.

9.3 Второй вид дифференциального уравнения неравномерного движения воды.

Преобразуем уравнение (9.12), причём введём в это уравнение глубину потока h. Полагая величину Q и русло заданными, рассмотрим отдельно каждый из членов уравнения (9.12).

1. Член I (пьезометрический уклон). Представим на рис. 9.9 продольный разрез потока. Из чертежа видно, что

где постоянная величина a – возвышение начала координат над плоскостью сравнения OO.

Очевидно,

откуда

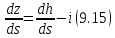
Пьезометрический уклон

Подставляя (9.15) в (9.16), окончательно для уклона I получаем зависимость

2. Член 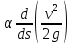. Выражая через расход Q, получаем

Рис. 9.9. К выводу формулы (9.17)

В данном случае мы рассматриваем нецилиндрическое русло. Поэтому площадь живого сечения ω зависит от двух координат: h и s, т.е.

Имея это в виду, можем написать:

где B – ширина потока поверху (рис. 9.10)

Рис. 9.10. К доказательству соотношения (9.21)

Подставляя (9.20) в (9.18), получаем окончательно

3. Член . Этот член можно представить в виде:

4. Подставляя теперь найденные выражения (9.17), (9.22) и (9.23) в (9.12), получаем:

решая это уравнение в отношении , окончательно имеем:

Уравнение (9.24) является вторым видом дифференциального уравнения неравномерного движения; оно относится к общему случаю нецилиндрического русла. Как видно, при помощи этого уравнения можно выразить приращение глубины потока dh на элементарной длине его ds. Подчеркнём, что уравнение (9.24) относится к случаю Q = const (вдоль потока).

Далее рассмотрим случай неравномерного движения воды в цилиндрических руслах.