2. Мероприятия по уменьшению скорости .

Скорость . Как видно, чтобы уменьшить , необходимо уменьшить или R, или C, или i. В соответствии с этим здесь приходится различать три разных приёма:

1) изменение формы поперечного сечения канала, чтобы несколько уменьшить гидравлический радиус; однако за счет изменения R не удаётся ощутимо снизить скорость ;

2) создание так называемой искусственной шероховатости, в результате чего повышается численное значение коэффициента шероховатости n и снижается численное значение коэффициента Шези C; этот приём в случае достаточно длинных каналов бывает неприемлем с экономической точки зрения;

3) уменьшение уклона i дна канала; обычно приходится обращаться именно к такому приёму; при этом по длине канала устраивают перепады. При этом продольный профиль дна канала принимает «пилообразный» вид. Участки между перепадами становятся более пологими, чем линия, параллельная поверхности земли;

4) иногда для уменьшения скорости каналам придают извилистую в плане форму или укладывают на дно специальные препятствия (например, в виде соломенных брёвен).

Необходимо заметить, что численные значения будут различны для случаев равномерного и неравномерного движения.

8.5 Расчёт каналов, имеющих замкнутый поперечный профиль.

Примерами каналов, имеющих замкнутый поперечный профиль, могут являться: а) канализационные трубы; б) дренажные трубы; в) водопропускные трубы (кулверты) под дорогами; г) гидротехнические туннели. Эти водотоки работают как безнапорные, поэтому с гидравлической точки зрения они ничем не отличаются от открытых каналов.

Рис. 8.8.

1. Канализационные трубы.

Канализационные трубы могут иметь различное поперечное сечение. Наиболее распространены трубы, имеющие круглое поперечное сечение.

Обозначим через h глубину наполнения трубы и через D полную её высоту. Отношение

называется степенью наполнения. В практике обычно принимают:

Замкнутые профили характеризуются следующей особенностью.

Представим на рис. 8.9 замкнутый профиль любого очертания. Предположим, что при i = const глубина наполнения этого профиля изменяется в пределах от h = 0 до h = D. При этом средняя скорость и расход Q будут также изменяться от нуля до некоторых значений и , отвечающих полному наполнению рассматриваемого канала.

Рис. 8.9

Существенным является то обстоятельство, что функции; в случае замкнутых профилей имеют максимум, чего не наблюдаем для обычных открытых русел.

Непосредственными подсчётами по формуле Шези было показано, что:

а) глубина h₁, отвечающая , лежит обычно в пределах:

б) глубина же h₂, при которой мы получаем , лежит обычно в пределах:

Как видно, некоторый расход Q, находящийся в пределах

имеет место в случае равномерного движения воды в трубе при двух различных глубинах: h’<h₂ и h’’>h₂. Таким образом, при расходе, лежащем в указанных пределах, возможно изменение условий протекания воды: глубина h’ может «переключаться» в глубину h’’ и наоборот.

Наличие максимума расхода в случае замкнутых профилей с физической точки зрения может быть объяснено следующим образом: представим себе наполнение трубы h только немногим меньше высоты трубы D; дадим далее величине h малое приращение ; при таком приращении глубины h благодаря тому, что горизонт воды стоит почти у самого замка свода, получим ничтожно малое приращение живого сечения ω, однако смоченный периметр, определяющий поверхность трения, увеличится значительно. В результате увеличения χ скорость уменьшится, и это уменьшение скорости будет более существенным, чем увеличение ω.

Следует, однако, иметь в виду, что всё сказанное выше получается в результате формального анализа зависимости Шези, без учета того обстоятельства, что между свободной поверхностью и замком свода имеется воздушная прослойка (прослойка «газообразной жидкости»), которая тоже приходит в движение при движении воды в трубе. Наличие этой воздушной прослойки, обусловливающей возникновение на свободной поверхности потока соответствующих сил трения, в некоторой мере искажает описанную выше картину движения воды.

Обратимся к расчету канализационных труб.

Для канализационных труб Р.Р.Чугаев [1] рекомендует принимать коэффициент шероховатости n равным

причём независимо от материала, из которого выполнены стенки труб, так как такие трубы с течением времени покрываются осадками, что в значительной мере сглаживает различие шероховатостей разных материалов.

Задачи, с которыми приходится сталкиваться при расчёте канализационных труб, следующие:

1) даны тип поперечного профиля и его размеры, а также величины a и i; требуется найти расход Q;

2) даны тип профиля и его размеры, а также величины a и Q; требуется найти уклон дна i и т.п.

Решение таких задач выполняется следующим образом.

1. Обозначим через K_п и W_п модули расхода и скорости, отвечающие полному заполнению трубы, когда h = D и a = 1. ; .

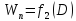2. Введём обозначения

где K и W – модули расхода и скорости, отвечающие действительной глубине h, имеющейся в трубе.

Оказывается, что величины M и N практически не зависят от размеров рассматриваемой трубы; как показывают соответствующие подсчёты, величины M и N зависят только от формы поперечного профиля трубы и от степени наполнения трубы a. Имея это в виду, в литературе даются графики для разных форм поперечного профиля труб, в частности, для кругового профиля ; .

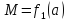3. Для расчета имеем известные формулы:

Эти формулы можно представить в виде

или в виде

Пользуясь формулами (8.30), а также таблицами и графиками и ведётся расчет. Например, требуется найти для трубы кругового профиля расход Q, если известны D, a, i. Для решения этой задачи поступаем следующим образом:

а) для заданного D по таблице находим ;

б) для заданного a по графику находим M и N;

в) по формулам (8.30) вычисляем , а также Q.