2.11 Уравнение Бернулли для газов.

Уравнение Бернулли для газов выводится из тех же дифференциальных уравнений, что и уравнение для капельных жидкостей. При этом учитывается взаимозависимость давления, плотности и температуры газа. Для самого общего случая политропического процесса уравнение Бернулли имеет вид

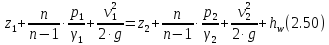
где n – показатель политропы; величина переменная, зависящая от условий теплообмена с окружающей средой. Как видим, величина γ в уравнении (2.50) для разных сечений отличается, так как давление вдоль потока уменьшается, соответственно и вес единицы объёма газа в направлении его движения также уменьшается.

Для адиабатического процесса в уравнении (2.50) вместо показателя политропы появляется показатель адиабаты

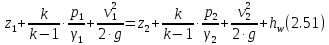
k для воздуха равно 1,4

При изотермическом процессе р/ρ = RT = const и уравнение Бернулли принимает вид:

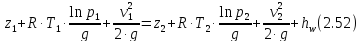
где R – удельная газовая постоянная, не зависящая от ρ и Т, но различная для разных газов (для воздуха R = 287 );

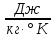Т – температура по шкале Кельвина (0°С = 273°К).

2.12 Гидравлическое уравнение количества движения для установившегося движения реальной жидкости.

Возьмём поток произвольной формы. Наметим два живых сечения 1-1 и 2-2.

Рис. 2.16

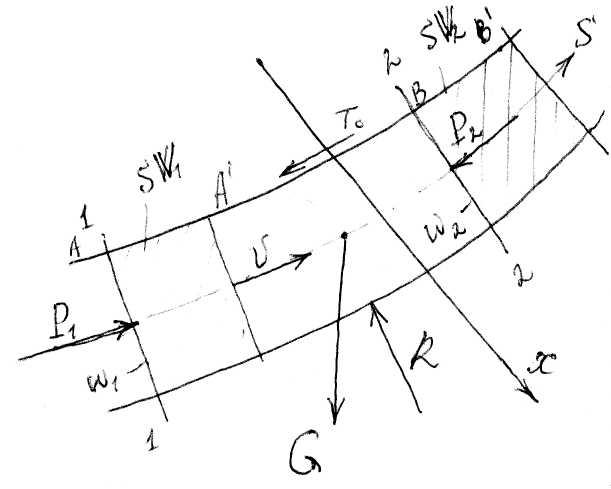
Покажем произвольную ось х. Поставим себе цель привести известную из теоретической механики теорему о количестве движения материальных точек к виду, удобному для расчета установившегося движения жидкости. Рассмотрим случай, когда в районе живых сечений 1-1 и 2-2 имеет место параллельноструйное или плавно изменяющееся движение (в промежутке между этими живыми сечениями может быть и резко изменяющееся движение). Дополнительно будем считать, что распределения скоростей u в сечениях 1-1 и 2-2 примерно одинаковы

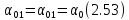
Напомним, что упомянутая теорема читается так: проекция на произвольно намеченную ось х приращения количества движения δ(КД) движущегося тела равна сумме проекций на ось х импульсов внешних сил (ИС), действующих на тело, за соответствующий промежуток времени. Данную теорему условно можно записать в виде:

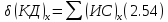
Применим эту теорему к отсеку жидкости АВ, заключенному в начальный момент времени между сечениями 1-1 и 2-2 и перемещающемуся за время dt в положение А’В’.

Приращения количества движения тела АВ.

Обозначим элементарные объёмы, заштрихованные на чертеже, соответственно δW₁ и δW₂. Очевидно,

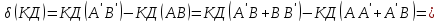
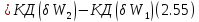
Известно, что количество движения (КД) тела равно произведению массы тела на его скорость.

Масса жидкости в объёме δW₁ есть та масса жидкости, которая за время dt проходит через сечение 1-1

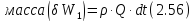
где ρ – плотность жидкости;

Q – расход жидкости.

Если бы все частицы жидкости проходили через живое сечение 1-1 с одинаковой скоростью 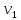, то количество движения КД(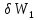) выразилось бы в виде:

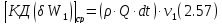
Так как в различных точках сечения 1-1 в действительности имеем разные скорости u, то искомое количество движения должно записаться в виде:

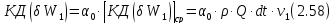
где 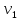- средняя скорость в живом сечении 1-1.

Аналогично для сечения 2-2 имеем:

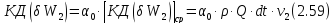
где 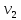- средняя скорость в живом сечении 2-2.

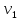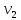Подставив (2.55) и (2.56) в (2.52) и заменив и проекциями этих скоростей на ось х, то есть величинам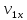и и 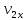, получаем

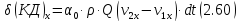
Импульсы внешних сил (ИС), приложенных к телу АВ.

Известно, что импульс силы равен произведению силы на время, в течение которого эта сила приложена к телу.

Рассмотрим все внешние силы, действующие на жидкое тело АВ при перемещении его в положение A’B’.

а) Сила собственного веса тела АВ.

Обозначим эту силу через G, а её проекцию на ось х через G_x. Проекция импульса этой силы равна

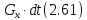
б) Сила внешнего трения Т₀, приложенная к боковой поверхности жидкого тела АВ со стороны боковых стенок, ограничивающих это тело. Проекция импульса этой силы равна

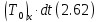
где 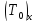- проекция данной силы на ось х.

в) Сила реакции боковых стенок, ограничивающих жидкое тело АВ. Проекция импульса этой силы равна

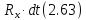
где 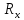- проекция данной силы на ось х.

г) Силы гидродинамического давления, действующие на торцевые сечения жидкого тела АВ (на сечения 1-1 и 2-2) со стороны остальной жидкости (силы Р₁ и Р₂). Проекция импульса этих двух сил

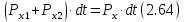
Подставляя в (2.54) выражения (2.61) – (2.64) и деля полученный результат на dt, получаем искомое выражение

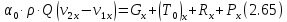
где - масса жидкости, проходящая в единицу времени (в секунду) через любое живое сечение потока, 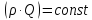(вдоль потока).

Проекция сил и скоростей, направленных против положительного направления оси x, должны иметь в уравнении (2.65) отрицательную величину.