Для обчислення десяткового логарифму “lg X” використовується формула [32]:
(3.12)
Рис.3.2. Графік функції десяткового логарифму y = lg x
для від’ємних значень логарифму
У довіднику з математики (Бронштейн І.Н., Семендяєв К.А.)[32] наведені також такі корисні співвідношення для логарифмів, в даному випадку десяткових :
(3.13)
(3.14)
Ці формули, а також графік значень десяткового логарифму для значень аргументу логарифму в діапазоні від одиниці до десяти, наведений на рис.3.3, значно спрощує процедуру розрахунку довільних десяткових логарифмів з урахуванням формули (3.13), яка для конкретних значень розписана в таблиці 3.2.
Таблиця 3.2
Процедура розрахунку десяткового логарифму
з урахуванням формули (3.13)
lg(x×z) |
x |
z |
lg x |
lg z |
lg x+ lg z |
lg 5 |
5 |
1 |
≈ 0.7 |
0 |
≈ 0.7 |
lg 50 |
5 |
10 |
≈ 0.7 |
1 |
≈ 1.7 |
lg 500 |
5 |
100 |
≈ 0.7 |
2 |
≈ 2.7 |
lg 5000 |
5 |
1000 |
≈ 0.7 |
3 |
≈ 3.7 |
lg 0.5 |
5 |
0.1 |
≈ 0.7 |
-1 |
≈ -0.3 |
lg 0.05 |
5 |
0.01 |
≈ 0.7 |
-2 |
≈ -1.3 |
lg 0.005 |
5 |
0.001 |
≈ 0.7 |
-3 |
≈ -2.3 |
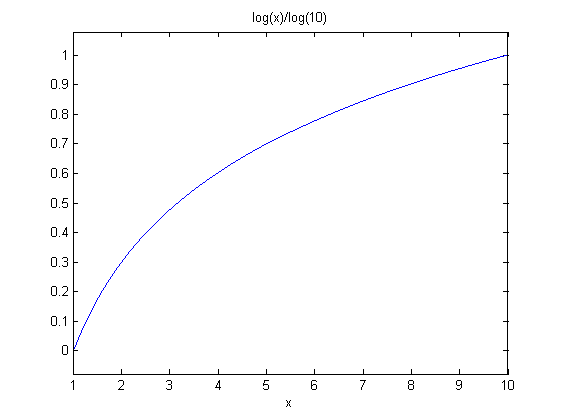
Рис.3.3. Графік функції десяткового логарифму y = lg xдля
значень аргументу логарифму в діапазоні від одиниці до десяти
Значення логарифму для х=5,4 приблизно дорівнює 0,73.
Значення десяткової логарифмічної функції для відношення I/I0 , що збільшене в 10 разів (ця величина дає “рівень інтенсивності звуку”, або “рівень сили звуку”,що позначається як L ( від англ.level – рівень) та вимірюється в децибелах, наведено в таблиці 3.3. Динамічний діапазон зміни рівня сили звуку змінюється від –20 до +140 дБ, що відповідає зміні сили звуку в навколишньому середовищі у 1016 разів. У подальшому, якщо це необхідно, рівень інтенсивності звуку будемо також позначати як LI (див. Табл.3.3) на відміну від рівня тиску Lp (див. Табл.3.4)
Таблиця 3.3
Таблиця переводу “інтенсивності” в “ рівні інтенсивності” LI
I |
10-14 |
10-13 |
10-12 |
10-11 |
… |
10+1 |
10+2 |
I/ I0 |
10-2 |
10-1 |
1 |
10+1 |
… |
10+13 |
10+14 |
LI=10×lg(I/ I0), дБ |
-20 |
-10 |
0 |
+10 |
|
+130 |
+140 |
Об'єктивною інтегральною характеристикою величини звукових коливань, яка також не враховує частотного складу звуку, є “тиск” звуку.
Тиск звуку Р в певній точці простору визначається як:
Р = Ра.м.– Ра.с. , де (3.15)
Ра..м. – миттєве значення тиску в точці простору під дією звукової хвилі;
Ра.с. – статичне атмосферне значення тиску в точці простору, коли звукової хвилі нема.
Тиск звукової хвилі характеризує величину “розрідження” або “згущення” повітря в певній точці простору. Тиск звуку Р вимірюється в Па (Паскаль – одиниця величини тиску). Минімальний тиск звуку Р0 , який ще відчуває людина, дорівнює приблизно 10-5 Па, максимальний тиск звуку Р, який ще людина здатна сприймати без значних больових відчуть, дорівнює приблизно 10+2 Па.
Таблиця 3.4
Таблиця переводу “тиску” в “рівень тиску” Lp
Р (Па) |
10-5 |
10-4 |
10-3 |
10-2 |
10+1 |
10+2 |
Р / Р0 |
1 |
10+1 |
10+2 |
10+3 |
10+6 |
10+7 |
Lp =20×lg(Р/ Р0), дБ |
0 |
+20 |
+40 |
+60 |
+120 |
+140 |
Коефіцієнт “20”, що використовується при обчисленні рівня Lp “тиску звуку” Р в децибелах, пояснюється так. Між інтенсивністю звуку І та звуковим тиском Р існує такий зв'язок:
І = Р 2 / (с×ρ) , де (3.16)
с – швидкість звуку в повітрі,
ρ – питома густина повітря. Тоді:
10×lg (І/І0) = 10×lg (Р/Р0)2 = 20× lg (Р/Р0). (3.17)
Співвідношення (3.17) безпосередньо виникають з формули (3.13), якщо позначити співвідношення (Р/Р0) = х та представити формулу (3.13) у такому вигляді:
(3.18)
Як закон Вебера-Фехнера, так і закон Стівенса походять із диференціальних співвідношень, для розкриття змісту яких і були введені такі поняття як рівень інтенсивності звуку та рівень звукового тиску.
Отже, якщо закон Вебера-Фехнера пов’язує рівень відчуття сприйняття звуку з рівнем інтенсивності, то закон Стівенса пов’язує величину відчуття сприйняття звуку безпосередньо з величиною інтенсивності звуку.