Метод Милна

Относится к группе методов прогноза-коррекции, в которых две различные формулы объединяются в один метод, действующий по схеме:

явной формулой предварительно вычисляется (прогнозируется) «грубое» значение y_n+1;

неявной формулой уточняется (корректируется) это значение.

Построение метода ф ормула прогноза

• Рассматриваемый интервал .

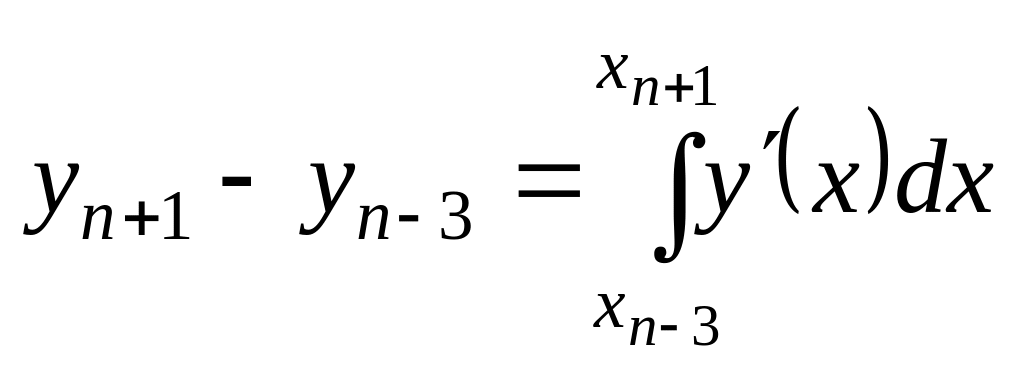• Интерполяционный полином для

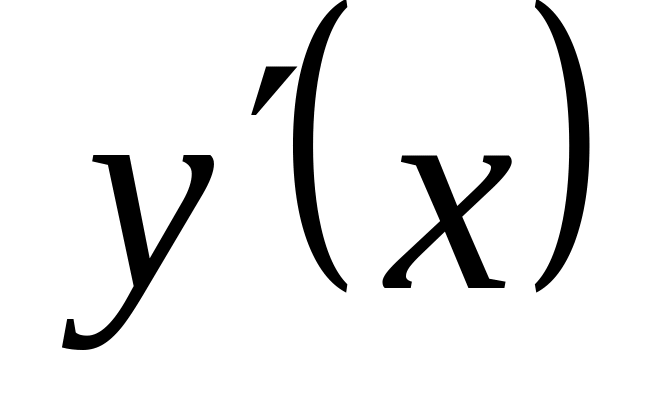
, где (Первая интерполяционная формула Ньютона).

• Замена переменной интегрирования

.

• Замена интерполяционным полиномом 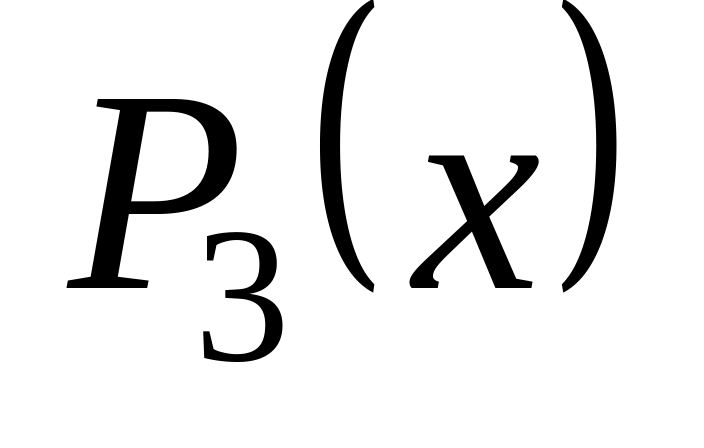и вычисление интеграла

.

• Замена конечных разностей значениями производной

; ;

;

;

­­­;

. .

Формула коррекции

.

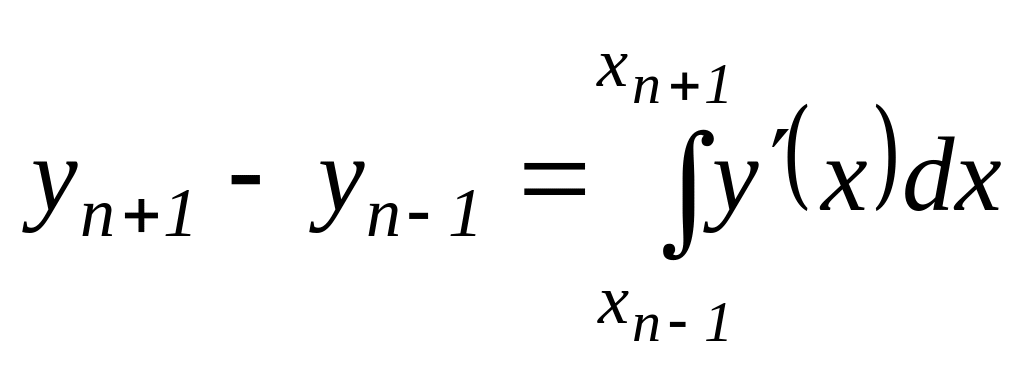С учётом квадратурной формулы Симпсона

.

Вспомогательная таблица (табл. 6.4):

Таблица 6.4

x	yпр	y'пр	yкор	y'кор
…	…	…	…	…

Постановка задачи

Необходимо решить дифференциальное уравнение с начальным условием методом:

1. Эйлера;

2. уточнённым Эйлера;

3. Рунге  Кутта (4 -го порядка);

4. Адамса;

5. Милна.

Варианты заданий

Вариант	Дифференциальное уравнение	Начальное условие	Отрезок интегри-рования	Точное решение
1	2	3	4	5
1				;
2				;
3				;
4				;
5				;
6				;
7				;
8				;
9				;
10				;
11				;
1	2	3	4	5
12				;
13				;
14				;
15				;
16				;
17				;
18
19				;
20				;
21				;
22				;
23				;
24				;
25				;
26				;
27				;
28				;
29				;
30				;
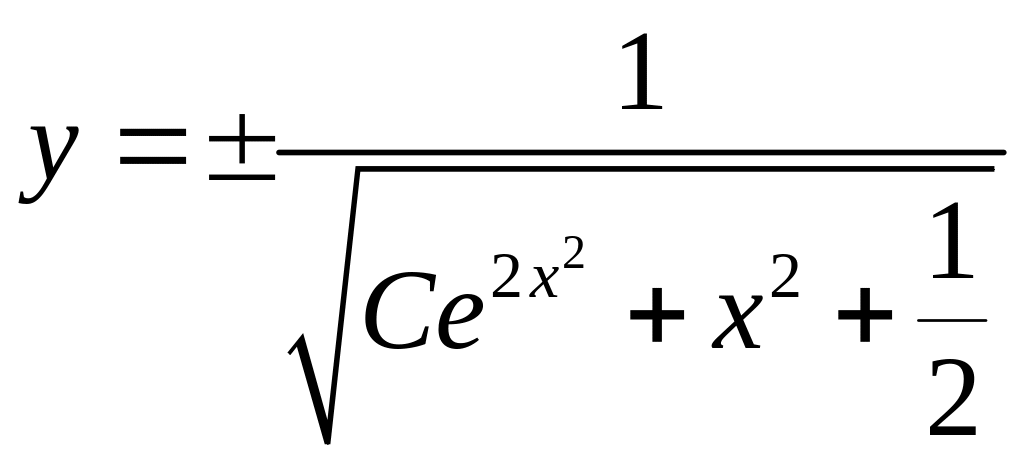